НОУ ИНТУИТ | Моделирование систем. Лекция 4: Выборочный метод Монте-Карло

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3338 / 2035 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Цель работы: Изучить и практически освоить метод Монте-Карло на примерах расчета площадей плоских фигур, объемов пространственных тел, а также вычисления кратных интегралов. Среда программирования — MATLAB.

Ключевые слова: метод статистических испытаний, оценка математического ожидания, нормальное распределение, стандартное отклонение, функция ошибок, случайная величина, определенный интеграл, псевдослучайное число, Относительной погрешностью, коллинеарность

Теоретическая часть

Сущность метода Монте-Карло состоит в следующем: требуется найти значение некоторой изучаемой величины. Для этого выбирают такую случайную величину , математическое ожидание которой равно , т. е. М(Х) = а [6].

Практически же поступают следующим образом: производят испытаний, в результате которых получают возможных значений величины ; вычисляют их среднее арифметическое

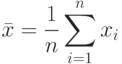
$\bar{x}=\frac{1}{n}\sum\limits_{i=1}^{n} x_i$

и принимают $\bar{x}$ в качестве оценки (приближенного значения) 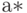искомого числа : $a\approx a^{*} =\bar{x}$ .

Поскольку метод Монте-Карло требует произведения большого числа испытаний, его часто называют методом статистических испытаний.

1. Оценка погрешности метода Монте-Карло

Как отмечалось, для получения оценки математического ожидания случайной величины необходимо произвести независимых испытаний и по ним найти выборочную среднюю, которая принимается в качестве искомой оценки. При каждой конечной серии испытаний будут получаться различные значения случайной величины и, следовательно, другая средняя, а значит, и другая оценка математического ожидания. Очевидно, что получить точную оценку математического ожидания невозможно. Поэтому возникает вопрос о допускаемой ошибке. Обычно ограничиваются отысканием лишь верхней границы $\delta$ допускаемой ошибки с заданной вероятностью $\gamma$ , т. е.

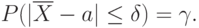
$P(|\overline{X}-a|\le\delta)=\gamma.$

При этом возможны следующие случаи оценки числа испытаний:

Случайная величина распределена нормально и ее среднее квадратическое отклонение (стандартное отклонение) $\delta$ известно. В этом случае с заданной вероятностью $\gamma$ верхняя граница ошибки определяется по формуле

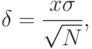
$\delta=\frac{x\sigma}{\sqrt{N}},$ ( 4.1)

где:

— число испытаний (разыгранных значений случайной величины );

— значение аргумента функции Лапласа или интеграла вероятности, при котором она равна половине заданной вероятности;

$\sigma$ — известное среднее квадратическое отклонение.

Из формулы (4.1) может быть найдено число испытаний. Один из вариантов интеграла вероятностей (функции Лапласа) имеет вид [6]

$Ф(х) = \frac{1}{\sqrt{2\pi}}\int\limits_{0}^{x}e^{-t^2 /2} dt.$ ( 4.2)

Значения табулированы и приведены в большинстве учебников по теории вероятностей и математической статистике.

В зарубежной литературе большое распространение получила так называемая функция ошибок ( ) :

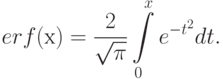
$erf(х) = \frac{2}{\sqrt{\pi}}\int\limits_{0}^{x}e^{-t^2} dt.$ ( 4.3)

Связь между функцией ошибок (4.3) и интегралом вероятностей (4.2) выражается в виде

$Ф(х) = 0.5 erf(x/\sqrt{2}).$ ( 4.4)
Случайная величина распределена нормально, причем ее среднее квадратическое отклонение неизвестно. В этом случае с заданной вероятностью $\gamma$ верхняя граница ошибки вычисляется по формуле

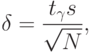
$\delta=\frac{t_{\gamma}s}{\sqrt{N}},$ ( 4.5)

где:

— число испытаний;

— "исправленное" среднее квадратическое отклонение;

$t_{\gamma}$ находят по специальным таблицам, например, приведенной в [6].

Из формулы (4.5) может быть найдено число испытаний для определения верхней границы ошибки.
Случайная величина распределена по закону, отличному от нормального. В этом случае при достаточно большом числе испытаний ( ), с вероятностью, приближенно равной $\gamma$ (заданной вероятностью), верхняя граница ошибки может быть вычислена по формуле (4.1), если среднее квадратическое отклонение случайной величины известно; если же оно неизвестно, то можно подставить в формулу (4.1) его оценку — "исправленное" среднее квадратическое отклонение — либо воспользоваться формулой (4.5). При этом чем больше число испытаний, тем меньше различие между результатами, которые дают обе формулы.

2. Вычисление кратных интегралов методом Монте-Карло

В случае когда, например, определенный интеграл не может быть вычислен в квадратурах, либо прибегают к численным методам интегрирования, либо расчет ведется с помощью метода Монте-Карло. Применение метода Монте-Карло становится оправданным при кратности интеграла больше трех. В данной лабораторной работе мы используем метод Монте-Карло для расчета интегралов с кратностью не более трех. Это позволит более ясно представить технику применения метода.

Сначала рассмотрим вычисление простого определенного интеграла

$I=\int\limits_{a}^{b}f(x)dx$

( 4.6)

где $b \ne a$ .

Введем под знак интеграла постоянный множитель (равный единице):

$\frac{b-a}{b-a},\\I=\int\limits_{a}^{b}f(x)\frac{b-a}{b-a}dx.$

( 4.7)

Вынесем из-под интеграла числитель дроби, получим

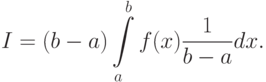$I=(b-a)\int\limits_{a}^{b}f(x)\frac{1}{b-a}dx.$

( 4.8)

Как известно, если случайная величина распределена на заданном интервале (например, b – a ) равномерно, то ее функция плотности p(x) обратно пропорциональна длине интервала, т. е.

$p(x)=\frac{1}{b-a}.$

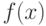Кроме того, если известно распределение случайной величины , то функция от этой случайной величины f(x) будет иметь тот же самый закон распределения. В этом случае математическое ожидание M[x] непрерывной равномерно распределенной случайной величины рассчитывается по формуле

$M[x]=\int\limits_{a}^{b}x\frac{1}{b-a}dx.$

Соответственно, математическое ожидание от функции случайной величины будет определяться следующим образом:

$M[f(x)]=\int\limits_{a}^{b}f(x)\frac{1}{b-a}dx.$

( 4.9)

Сопоставляя (4.8) и (4.9), приходим к выводу, что определенный интеграл может быть рассчитан по формуле

( 4.10)

Несмещенной оценкой математического ожидания случайной величины, как известно, является ее среднее арифметическое. Поэтому математическое ожидание можем приближенно найти по формуле

$M[f(x)]\approx \frac{1}{n}\sum\limits_{i=1}^{n}f(x_i).$

( 4.11)

С учетом (4.11) получаем выражение для приближенного расчета определенного интеграла

$I\approx \frac{b-a}{n}\sum\limits_{i=1}^{n}f(x_i).$

( 4.12)

Чем больше число испытаний , тем точнее будет расчет математического ожидания (4.11) и, следовательно, определенного интеграла, вычисляемого по формуле (4.12).

Рассмотрим общий подход вычисления 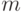-кратного интеграла с помощью метода Монте-Карло [5].

Пусть задан 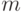-кратный интеграл вида

$I=\mathop{\int\int ... \int}\limits_{D} f(x_1,x_2,...,x_m)dx_1dx_2...dx_m,$

( 4.13)

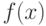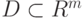где подынтегральная функция f(x) задана на замкнутой области $D \subset R^m$ .

Погрузим область интегрирования 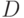в 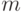-мерный промежуток

$D^* = [a_1, b_1]\times[a_2, b_2]\times ... [a_m, b_m],$

( 4.14)

имеющий меру

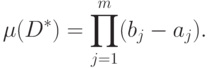$\mu(D^*)=\prod\limits_{j=1}^{m}(b_j-a_j).$

( 4.15)

Определим в промежутке (4.15) функцию

$g(x)=\begin{cases} f(x),&x\in D;\\ 0, &x \in D^* \setminus D.\\ \end{cases}$

( 4.16)

Тогда в соответствии с (4.13) и (4.16) получим

$I=\mathop{\int\int ... \int}\limits_{D^*} g(x_1,x_2,...,x_m)dx_1dx_2...dx_m,$

( 4.17)

Введем в рассмотрение 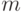-мерную случайную величину , имеющую в замкнутой области равномерное распределение вероятностей с дифференциальной функцией плотности

$p(x)=\frac{1}{\mu (D^*)}$

( 4.18)

Функция плотности равномерного распределения есть величина постоянная, поэтому введем ее под знак интеграла (4.17) следующим образом:

$I=\mathop{{\int\int ... \int} g(x_1,x_2,...,x_m)}\limits_{D^*}\frac{\mu (D^{*})}{\mu (D^{*})}dx_1dx_2...dx_m,$

( 4.19)

Вынесем числитель дроби за знак интеграла, т. е.

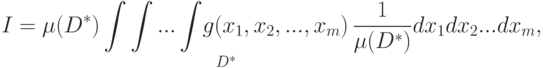$I=\mu (D^{*})\mathop{{\int\int ... \int} g(x_1,x_2,...,x_m)}\limits_{D^*}\frac{1}{\mu (D^{*})}dx_1dx_2...dx_m,$

( 4.20)

В (4.20) 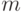-кратный интеграл — это математическое ожидание от функции g(x) случайной величины в предположении, что случайная величина распределена равномерно с плотностью (4.18). Следовательно, можем записать

$I=\mu (D^{*})M[g(x)],$

( 4.21)

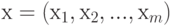где $х = (х_{1}, х_{2}, ... , х_{m})$ .

В свою очередь математическое ожидание может быть оценено с помощью арифметического среднего. Тогда приближенное значение 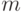-кратного интеграла будет определяться приближенной формулой

$I\approx \frac{\mu (D^{*})}{N}\sum\limits_{k=1}^{N}g(x^{(k)}),$

( 4.22)

где $x^{(k)} \in D^{*}$ — значение случайной величины в -м испытании.

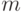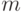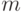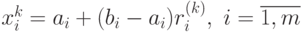Чтобы смоделировать выборку -мерной случайной величины , равномерно распределенной в -мерном промежутке $D^{*}$ , используются псевдослучайные числа. Для этого в каждом испытании с номером выбирают псевдослучайных чисел $r_i^{(k)},\mbox{ }i=\overline{1,m}$ , и по ним определяют координаты случайной величины $x_i^{k}=a_i+(b_i-a_i)r_i^{(k)},\mbox{ }i=\overline{1,m}$ , псевдослучайной точки $x^{(k)}$ [5].

Таким образом, техника применения метода Монте-Карло здесь будет заключаться в определении области $D^{*}$ , генерировании в ней псевдослучайных чисел, подсчета числа попаданий этих чисел в область 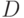и применении формулы (4.22).

Расчет площадей и объемов можно рассматривать как частный случай вычисления кратных интегралов. Например, вычисление объема тел с помощью трехкратного интеграла сводится к взятию интеграла по области при подынтегральной функции, тождественно равной единице.

Дальше >>

Авторизоваться

Моделирование систем

Выборочный метод Монте-Карло

Теоретическая часть

1. Оценка погрешности метода Монте-Карло

2. Вычисление кратных интегралов методом Монте-Карло

Вопросы и ответы