Статистика интервальных данных

12.2. Интервальные данные в задачах оценивания характеристик и параметров распределения

Поясним теоретические концепции статистики интервальных данных на простых примерах.

Пример 1. Оценивание математического ожидания. Пусть необходимо оценить математическое ожидание случайной величины с помощью обычной оценки - среднего арифметического результатов наблюдений, т.е.

Тогда при справедливости ограничений (1) на абсолютные погрешности имеем . Таким образом, нотна полностью известна и не зависит от многомерной точки, в которой берется. Вполне естественно: если каждый результат наблюдения известен с точностью до , то и среднее арифметическое известно с той же точностью. Ведь возможна систематическая ошибка - если к каждому результату наблюдения добавить , то и среднее арифметическое увеличится на .

Поскольку

то в обозначениях предыдущего параграфа

Следовательно, рациональный объем выборки равен

Для практического использования полученной формулы надо оценить дисперсию результатов наблюдений. Можно доказать, что, поскольку мало, это можно сделать обычным способом, например, с помощью несмещенной выборочной оценки дисперсии

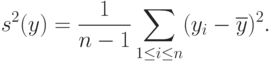
Здесь и далее рассуждения часто идут на двух уровнях. Первый - это уровень "истинных" случайных величин, обозначаемых " ", описывающих реальность, но неизвестных специалисту по анализу данных. Второй - уровень известных этому специалисту величин " , отличающихся погрешностями от истинных. Погрешности малы, поэтому функции от отличаются от функций от на некоторые бесконечно малые величины. Эти соображения и позволяют использовать 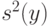как оценку .

Итак, выборочной оценкой рационального объема выборки является

Уже на этом первом рассматриваемом примере видим, что рациональный объем выборки находится не где-то вдали, а непосредственно рядом с теми объемами, с которыми имеет дело любой практически работающий статистик. Например, если статистик знает, что , то . А именно такова погрешность контрольных шаблонов во многих технологических процессах! Поэтому, занимаясь управлением качества, необходимо обращать внимание на действующую на предприятии систему измерений.

По сравнению с классической математической статистикой доверительный интервал для математического ожидания (для заданной доверительной вероятности 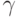) имеет другой вид:

где - квантиль порядка 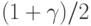стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

По поводу формулы (4) состоялась довольно жаркая дискуссия среди специалистов (ср. 8.1). Отмечалось, что она получена на основе Центральной предельной теоремы теории вероятностей и может быть использована при любом распределении результатов наблюдений (с конечной дисперсией). Если же имеется дополнительная информация, то, по мнению отдельных специалистов, формула (4) может быть уточнена. Например, если известно, что распределение является нормальным, в качестве целесообразно использовать квантиль распределения Стьюдента. К этому надо добавить, что по небольшому числу наблюдений нельзя надежно установить нормальность, а при росте объема выборки квантили распределения Стьюдента приближаются к квантилям нормального распределения. Вопрос о том, часто ли результаты наблюдений имеют нормальное распределение, подробно обсуждался среди специалистов. Выяснилось, что распределения встречающихся в практических задачах результатов измерений почти всегда отличны от нормальных [ [ 12.30 ] ]. А также и от распределений из иных параметрических семейств, описываемых в учебниках.

Применительно к оцениванию математического ожидания (но не к оцениванию других характеристик или параметров распределения) факт существования границы возможной точности, определяемой точностью исходных данных, неоднократно отмечался в литературе ([ [ 12.11 ] , с.121] и др.).

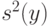Пример 2. Оценивание дисперсии. Для статистики , где - выборочная дисперсия (несмещенная оценка теоретической дисперсии), при справедливости ограничений (1) на абсолютные погрешности имеем

Можно показать, что нотна сходится к по вероятности с точностью до , когда стремится к бесконечности. Это же предельное соотношение верно и для нотны , вычисленной для исходных данных. Таким образом, в данном случае справедлива формула (2) с .

Известно, что случайная величина

является асимптотически нормальной с математическим ожиданием 0 и дисперсией .

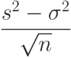
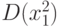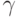Из сказанного вытекает, что в статистике интервальных данных асимптотический доверительный интервал для дисперсии (соответствующий доверительной вероятности ) имеет вид

где обозначает тот же самый квантиль стандартного нормального распределения, что и выше в случае оценивания математического ожидания.

Рациональный объем выборки при оценивании дисперсии равен

а выборочную оценку рационального объема выборки можно вычислить, заменяя теоретические моменты на соответствующие выборочные и используя доступные статистику результаты наблюдений, содержащие погрешности.

Что можно сказать о численной величине рационального объема выборки? Как и в случае оценивания математического ожидания, она отнюдь не выходит за пределы обычно используемых объемов выборок. Так, если распределение результатов наблюдений является нормальным с математическим ожиданием 0 и дисперсией , то в результате вычисления моментов случайных величин в предыдущей формуле получаем, что

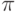где - отношение длины окружности к диаметру, .. Например, если , то . Это меньше, чем при оценивании математического ожидания в предыдущем примере.

Пример 3. Аддитивные статистики. Пусть - некоторая непрерывная функция. Аддитивные статистики имеют вид

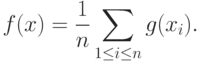
Тогда

по вероятности при , если математические ожидания в правых частях двух последних соотношений существуют. Применяя рассмотренные выше общие соображения, получаем, что при малых фиксированных и 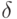и достаточно больших значения 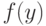могут принимать любые величины из разрешенных (например, записываемых заданным числом значащих цифр) в замкнутом интервале при ограничениях (1) на абсолютные ошибки и в замкнутом интервале при ограничениях на относительные погрешности результатов наблюдений. Обратим внимание, что длины этих интервалов независимы от объема выборки, в частности, не стремятся к 0 при его росте.

К каким последствиям это приводит в задачах статистического оценивания? Поскольку для статистик аддитивного типа

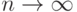по вероятности при , если математическое ожидание в правой части формулы (7) существует, то аддитивную статистику естественно рассматривать как непараметрическую оценку этого математического ожидания. Термин "непараметрическая" означает, что не делаются предположения о принадлежности функции распределения выборки к тому или иному параметрическому семейству распределения. Распределение статистики зависит от распределения результатов наблюдений. Однако для любого распределения результатов наблюдений с конечной дисперсией статистика является состоятельной и асимптотически нормальной оценкой для математического ожидания, указанного в правой части формулы (7).

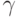Как известно, в рамках классической математической статистики в предположении существования ненулевой дисперсии в силу асимптотической нормальности аддитивной статистики асимптотический доверительный интервал, соответствующий доверительной вероятности , имеет вид

где - выборочное среднее квадратическое отклонение, построенное по , а - квантиль стандартного нормального распределения порядка .

В рассматриваемой модели порождения интервальных данных вместо необходимо использовать 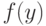, а вместо - соответственно . При этом доверительный интервал необходимо расширить с учетом формул (5) и (6).

В соответствии с проведенными рассуждениями для аддитивных статистик асимптотическая нотна имеет вид

при ограничениях (1) на абсолютную погрешность и при ограничениях на относительную погрешность. В первом случае нотна является обобщением понятия предельной абсолютной систематической ошибки, во втором - предельной относительной систематической ошибки. Отметим, что, как и в примерах 1 и 2, асимптотическая нотна не зависит от точки, в которой вычисляется. Таким образом, она является константой для конкретного метода статистического анализа данных.

Поскольку велико, а и 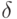малы, то можно пренебречь отличием выборочного среднего квадратического отклонения , вычисленного по выборке преобразованных значений от выборочного среднего квадратического отклонения , построенного по выборке 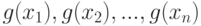. Разность этих двух величин является бесконечно малой, они приближаются к одной и той же положительной константе.

В статистике интервальных данных выборочный доверительный интервал для 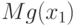имеет вид

В асимптотике его длина такова:

где - дисперсия 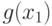, в то время как в классической теории математической статистики имеется только второе слагаемое. Соотношение (8) - аналог суммарной ошибки у метрологов. Поскольку первое слагаемое положительно, то оценивание 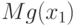с помощью 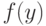не является состоятельным.

Для аддитивных статистик при больших максимум (по возможным погрешностям) среднего квадрата отклонения оценки имеет вид

с точностью до членов более высокого порядка. Исходя из принципа уравнивания погрешностей в общей схеме устойчивости [ [ 1.15 ] ], нецелесообразно второе слагаемое в (9) делать меньше первого за счет увеличения объема выборки . Рациональный объем выборки, т.е. тот объем, при котором равны погрешности оценивания (или проверки гипотез), вызванные погрешностями исходных данных, и статистические погрешности, рассчитанные по обычным правилам математической статистики (при ), для аддитивных статистик согласно (9) имеет вид

В качестве примера рассмотрим экспоненциально распределенные результаты наблюдений , причем . Оцениваем математическое ожидание с помощью выборочного среднего арифметического при ограничениях на относительную погрешность. Тогда согласно формуле (10)

В частности, если относительная погрешность измерений , то рациональный объем выборки равен 100. Формуле (10) соответствует также рассмотренный выше пример 1.

Пример 4. Оценивание медианы распределения с помощью выборочной медианы. Хотя нельзя выделить главный линейный член из-за недифференцируемости функции , выражающей выборочную медиану через элементы выборки, непосредственно из определения нотны следует, что при ограничениях на абсолютные погрешности

а при ограничениях на относительные погрешности с точностью до бесконечно малых более высокого порядка, где - теоретическая медиана. Доверительный интервал для медианы имеет вид где - доверительный интервал для медианы (см. 8.1), вычисленный по классическим правилам непараметрической статистики [ [ 12.38 ] ]. Для нахождения рационального объема выборки можно использовать асимптотическую дисперсию выборочной медианы. Она, как известно (см., например, [ [ 12.13 ] , с.178]), равна где - плотность распределения результатов измерений в точке . Следовательно, рациональный объем выборки имеет вид при ограничениях на абсолютные и относительные погрешности результатов измерений соответственно. Для практического использования этих формул следует оценить плотность распределения результатов измерений в одной точке - теоретической медиане. Это можно сделать с помощью тех или иных непараметрических оценок плотности (см. 5.6 и [ [ 12.38 ] ]).

Если результаты наблюдений имеют стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1, то

В этом случае рациональный объем выборки в раз больше, чем для оценивания математического ожидания (пример 1 выше). Однако для других распределений рассматриваемое соотношение объемов может быть иным, в частности, меньше 1. Как вытекает из статьи А.Н.Колмогорова [ [ 12.18 ] ], рассматриваемое соотношение объемов может принимать любое значение между 0 и 3.

Пример 5. Оценивание коэффициента вариации. Рассмотрим выборочный коэффициент вариации

Как нетрудно подсчитать,

В случае ограничений на относительную погрешность

На основе этого предельного соотношения и формулы для асимптотической дисперсии выборочного коэффициента вариации, приведенной в 8.1 и [ [ 12.38 ] ], могут быть найдены по описанной выше схеме доверительные границы для теоретического коэффициента вариации и рациональный объем выборки.

Замечание. Отметим, что формулы для рационального объема выборки получены на основе асимптотической теории, а применяются для получения конечных объемов - 11, 36 и 100 в примерах 1-3. Как всегда при использовании асимптотических результатов математической статистики, необходимы дополнительные исследования для изучения точности асимптотических формул при конечных объемах выборок.

Рассмотрим классическую в прикладной математической статистике параметрическую задачу оценивания. Исходные данные - выборка , состоящая из n действительных чисел. В вероятностной модели простой случайной выборки ее элементы , считаются набором реализаций независимых одинаково распределенных случайных величин. Будем считать, что эти величины имеют плотность . В параметрической статистической теории предполагается, что плотность известна с точностью до конечномерного параметра, т.е., 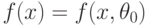при некотором . Это, конечно, весьма сильное предположение, которое требует обоснования и проверки; однако в настоящее время параметрическая теория оценивания широко используется в различных прикладных областях.

Все результаты наблюдений определяются с некоторой точностью, в частности, записываются с помощью конечного числа значащих цифр (обычно 2-5). Следовательно, все реальные распределения результатов наблюдений дискретны. Обычно считают, что эти дискретные распределения достаточно хорошо приближаются непрерывными. Уточняя это утверждение, приходим к уже рассматривавшейся модели, согласно которой статистику доступны лишь величины

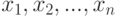где - "истинные" значения, - погрешности наблюдений (включая погрешности дискретизации). В вероятностной модели принимаем, что пар образуют простую случайную выборку из некоторого двумерного распределения, причем - выборка из распределения с плотностью 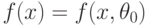. Необходимо учитывать, что и - реализации зависимых случайных величин (если считать их независимыми, то распределение будет непрерывным, а не дискретным). Поскольку систематическую ошибку, как правило, нельзя полностью исключить, то необходимо рассматривать случай . Нет оснований априори принимать и нормальность распределения погрешностей (согласно сводкам экспериментальных данных о разнообразии форм распределения погрешностей измерений, приведенным в [ [ 12.38 ] , с.71-77], в подавляющем большинстве случаев гипотеза о нормальном распределении погрешностей оказалась неприемлемой для средств измерений различных типов). Таким образом, все три распространенных представления о свойствах погрешностей не адекватны реальности. Влияние погрешностей наблюдений на свойства статистических моделей необходимо изучать на основе иных моделей, а именно, моделей интервальной статистики.

Пусть - характеристика величины погрешности, например, средняя квадратическая ошибка . В классической математической статистике считается пренебрежимо малой при фиксированном объеме выборки . Общие результаты доказываются в асимптотике . Таким образом, в классической математической статистике сначала делается предельный переход 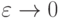, а затем предельный переход 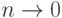. В статистике интервальных данных принимаем, что объем выборки достаточно велик , но всем измерениям соответствует одна и та же характеристика погрешности . Полезные для анализа реальных данных предельные теоремы получаем при 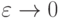. В статистике интервальных данных сначала делается предельный переход 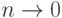, а затем предельный переход 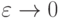. Итак, в обеих теориях используются одни и те же два предельных перехода: 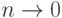и 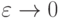, но в разном порядке. Утверждения обеих теорий принципиально различны.

В дальнейшем изложение идет на примере оценивания параметров гамма-распределения, хотя аналогичные результаты можно получить и для других параметрических семейств, а также для задач проверки гипотез (см. ниже) и т.д. Наша цель - продемонстрировать основные черты подхода статистики интервальных данных. Его разработка была стимулирована подготовкой ГОСТ 11.011-83 [ [ 12.12 ] ].

Отметим, что постановки статистики объектов нечисловой природы соответствуют подходу, принятому в общей теории устойчивости [ [ 1.15 ] , [ 12.38 ] ]. В соответствии с этим подходом выборке ставится в соответствие множество допустимых отклонений 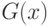, т.е. множество возможных значений вектора результатов наблюдений 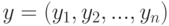. Если известно, что абсолютная погрешность результатов измерений не превосходит , то множество допустимых отклонений имеет вид

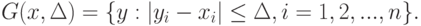
Если известно, что относительная погрешность не превосходит 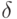, то множество допустимых отклонений имеет вид

Теория устойчивости позволяет учесть "наихудшие" отклонения, т.е. приводит к выводам типа минимаксных, в то время как конкретные модели погрешностей позволяют делать заключения о поведении статистик "в среднем".

Оценки параметров гамма-распределения. Как известно, случайная величина имеет гамма-распределение, если ее плотность такова [ [ 12.12 ] ]:

где - параметр формы, - параметр масштаба, - гамма-функция. Отметим, что есть и иные способы параметризации семейства гамма-распределений [ [ 12.35 ] ] (см также 6.1).

Поскольку , то оценки метода имеют вид

где - выборочное среднее арифметическое, а - выборочная дисперсия. Можно показать, что при больших с точностью до бесконечно малых более высокого порядка.

Оценка максимального правдоподобия имеет вид [ [ 12.12 ] ]:

где - функция, обратная к функции

При больших с точностью до бесконечно малых более высокого порядка

Как и для оценок метода моментов, оценка максимального правдоподобия параметра масштаба имеет вид

При больших с точностью до бесконечно малых более высокого порядка

Используя свойства гамма-функции, можно показать [ [ 12.12 ] ], что при больших

с точностью до бесконечно малых более высокого порядка. Сравнивая с формулами (11), убеждаемся в том, что средние квадраты ошибок для оценок метода моментов больше соответствующих средних квадратов ошибок для оценок максимального правдоподобия. Таким образом, с точки зрения классической математической статистики оценки максимального правдоподобия имеют преимущество по сравнению с оценками метода моментов.