НОУ ИНТУИТ | Введение в геометрическое программирование. Лекция 1: Неравенство Коши и его обобщения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Санкт-Петербургский государственный университет

Опубликован: 08.06.2009 | Доступ: свободный | Студентов: 663 / 131 | Оценка: 4.65 / 4.35 | Длительность: 07:44:00

Специальности: Программист

Теги: beta, базисными векторами, безопасность, вычисления, двойственная задача, задача линейного программирования, книги, линейное программирование, модель задач, обобщенный полином, оптимальное решение задачи, поддержка, программирование, рабочая книга, свойства множества, теория, форматы, число независимости

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Теорема 2 Решением экстремальной задачи

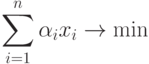
$\sum\limits_{i = 1}^{n}\alpha_{i}x_{i}\rightarrow \min$

при ограничениях

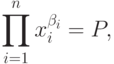
$\prod\limits_{i=1}^{n}x_{i}^{\beta_i}= P,$

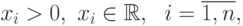
$x_i> 0,\ x_i\in\mathbb{R},\ \ i = \overline{1,n},$

где

$\alpha_i > 0,\ \beta_i >0,\ \beta_i\in\mathbb{R},\ \alpha_i\in\mathbb{R},\ i = \overline{1,n},$

является единственный вектор 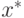$x^{*}$ с компонентами

$x_{i}^{*} = \frac{\beta_i}{\alpha_i} \left[P \prod\limits_{i=1}^{n}\left(\frac{\alpha_i}{\beta_i}\right)^{\beta_i} \right]^{1/\beta} = \frac{\beta_i}{\alpha_i}\ \frac{\mu}{\beta},\mbox{ где }\ \beta = \sum\limits_{i=1}^{n}\beta_i.$

( 11)

Минимум целевой функции $\mu$ вычисляется по формуле:

$\mu = \beta \left[ P\prod\limits_{i=1}^{n}\left(\frac{\alpha_i}{\beta_i}\right)^{\beta_i} \right]^{1/\beta}.$

( 12)

В следующем примере рассмотрена задача, обратная к задаче из примера 5. Для ее решения используется теорема 2.

Пример 6 Найдем, при каких наименьших затратах на ресурсы будет достигнут заданный объем выпуска продукции.

В обозначениях примера 5 математическая модель этой задачи примет вид:

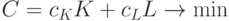
$C={c_K} K +{c_L} L\rightarrow \min$

при ограничениях

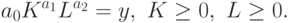$a_0 {K}^{a_1} {L}^{a_2}=y,\ K\geq 0,\ L\geq 0.$

( 13)

Преобразуем ограничение (13):

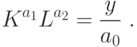
${K}^{a_1} {L}^{a_2}= \frac{y}{a_0}\ .$

Для решения этой задачи воспользуемся теоремой 2 при 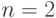n = 2 , x_1 =K , x_2 = L , $P=\frac{y}{a_0}$ , $\alpha_1 = c_K$ , $\alpha_2 = c_L$ , $\beta_1 = a_1$ , $\beta_2 = a_2$ .

Подставляя в формулу (11) значения параметров, получим оптимальные количества ресурсов:

$K^* =\frac{a_1}{c_K}{\left[ \frac{y}{a_0}\left(\frac{c_K}{a_1}\right)^{a_1} % \left(\frac{c_L}{a_2}\right)^{a_2}\right] }^{\frac{1}{a_1+a_2}}= \left(\frac{y}{a_0}\right)^{\frac{1}{a_1+a_2}}c_K^{\frac{-a_2}{a_1+a_2}}% c_L^{\frac{a_2}{a_1+a_2}}a_{1}^{\frac{a_2}{a_1+a_2}}a_{2}^{\frac{-a_2}{a_1+a_2}} =$

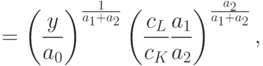
$={\left( \frac{y}{a_0} \right) }^{\frac{1}{a_1+a_2}} \left( \frac{c_L}{c_K} \frac{a_1}{a_2}\right)^{\frac{a_2}{a_1+a_2}},$

$L^* =\frac{a_2}{c_L}{\left[ \frac{y}{a_0}\left(\frac{c_K}{a_1}\right)^{a_1} \left(\frac{c_L}{a_2}\right)^{a_2}\right] }^{\frac{1}{a_1+a_2}}=\left(\frac{y}{a_0}\right)^{\frac{1}{a_1+a_2}}c_K^{\frac{a_1}{a_1+a_2}}c_L^{\frac{-a_1}{a_1+a_2}}a_{1}^{\frac{-a_1}{a_1+a_2}}a_{2}^{\frac{a_1}{a_1+a_2}} =$

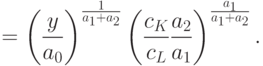
$= {\left(\frac{y}{a_0}\right)}^{\frac{1}{a_1+a_2}} \left(\frac{c_K}{c_L} \frac{a_2}{a_1}\right)^{\frac{a_1}{a_1+a_2}}.$

Наименьшие затраты 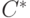C^* на ресурсы вычисляются по формуле (12):

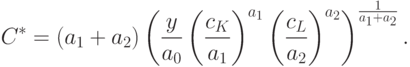
$C^*=(a_1+a_2) \left(\frac{y}{a_0}\left( \frac{c_K}{a_1}\right)^{a_1}\left( \frac{c_L}{a_2}\right)^{a_2}\right)^{\frac{1}{a_1+a_2}}.$

В двух последних примерах использовалась функция Кобба-Дугласа

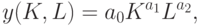
$y(K,L)= a_0 {K}^{a_1} {L}^{a_2},$

принадлежащая классу функций, к описанию которого мы переходим.

Заметим, что в этой лекции мы пока не приводим формальную постановку задачи геометрического программирования, но все рассматриваемые в ней примеры являются таковыми задачами или сводятся к ней с помощью простых преобразований.

Мономы

Мономом называется функция u(x) , которая определяется следующей формулой:

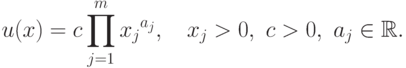$u(x)=c\prod\limits_{j=1}^{m}{x_{j}}^{a_{j}},\quad x_j>0,\ c >0, \ a_{j}\in \mathbb{R}.$

( 14)

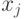Таким образом, моном - это произведение положительного коэффициента и переменных x_j в вещественных степенях $a_{j}$ . Эти степени образуют вектор экспонент монома, который мы будем обозначать через . Подчеркнем, что поскольку допускаются дробные и отрицательные показатели степеней, то область определения монома ограничена строго положительными вещественными числами.

Пример 7 Определим коэффициент и вектор экспонент следующего монома:

$u(x) = 5x_{1}^{2}x_{2}^{-3}.$

В моном входят две переменные: 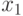x_1 и x_2 .

Коэффициент монома: c = 5 .

Вектор экспонент монома: $a = (2,\ -3)$ .

Перечислим основные свойства множества мономов:

если - моном, $\lambda >0$ - константа, то $\lambda u(x)$ - моном,
если - моном, - моном, то - моном,
если - моном, - моном, то - моном,
если - моном, то ${u(x)}^\alpha$ - моном ( $\alpha \in\mathbb{R}$ ).

Теперь мы переходим к описанию базового понятия в ГП - позиномам.

Позиномы

Позином называется обобщенный полином вида:

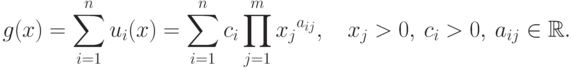$g(x)=\sum\limits_{i=1}^{n}u_{i}(x) = \sum\limits_{i=1}^{n}c_{i}\prod\limits_{j=1}^{m}{x_{j}}^{a_{ij}},\quad x_j>0,\ c_i>0, \ a_{ij}\in \mathbb{R}.$

( 15)

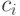Позином можно рассматривать как сумму мономов $u_{i}(x),\ i= \overline{1,n}$ . Коэффициенты c_i называют вектором коэффициентов позинома. Естественно, что область определения позинома (также как у монома) ограничена строго положительными вещественными числами.

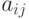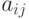Показатели степени $a_{ij}$ принято записывать в виде матрицы $A=\|a_{ij}\|$ , которую называют матрицей экспонент. Количество строк в матрице равно числу мономов (n) , а количество столбцов - числу переменных позинома (m) . Значение элемента $a_{ij}$ равно степени (экспоненте) переменной 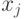x_j в мономе 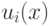u_i(x) ^{1Обращаем внимание читателя на тот факт, что
в ряде источников матрицей экспонент называют транспонированную матрицу .}

С целью записи формулы (15) в компактном виде введем следующее обозначение:

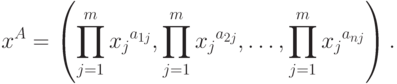
$x^A=\left(\prod\limits_{j=1}^{m}{x_{j}}^{a_{1j}}, \prod\limits_{j=1}^{m}% {x_{j}}^{a_{2j}}, \ldots, \prod\limits_{j=1}^{m}{x_{j}}^{a_{nj}}\right).$

С учетом введенного обозначения формула (15) может быть переписана в следующем виде:

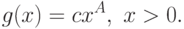$g(x)=cx^A,\ x>0.$

( 16)

Обозначим через 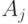A_j - столбец с номером матрицы . Тогда формула

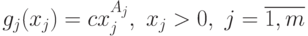$g_j(x_j)=cx_j^{A_j},\ x_j>0,\ j= \overline{1,m}$

( 17)

определяет позиномы от одной переменной g_j(x_j) , которые называются компонентами позинома g(x) .

Перечислим основные свойства множества позиномов:

если - позином, $\lambda >0$ - константа, то $\lambda g(x)$ - позином,
если - позином, - позином, то - позином,
если - позином, - моном, то - позином,
если - позином, - моном, то - позином,
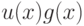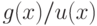если - позином, то ${g(x)}^k\ (k>0, \mbox{целое})$ - позином.

Раcсмотрим примеры позиномов.

Пример 8 Определим вектор коэффициентов и матрицу экспонент позинома

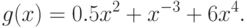
$g(x) = 0.5x^{2} + x^{-3} + 6x^{4}.$

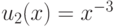В позином входит одна переменная . Позином состоит из трех мономов: $u_1(x) = 0.5x^{2}$ , $u_2(x) = x^{-3}$ , $u_3(x) = 6x^{4}$ . Вектор коэффициентов: c = (0. 5, 1, 6) . Матрицей экспонент позинома является ( $3\times 1$ )-матрица

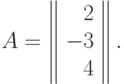
$A=\left\| \begin{array}{r} 2 \\ -3 \\ 4\\ \end{array} \right\|.$

Пример 9 Определим вектор коэффициентов и матрицу экспонент позинома

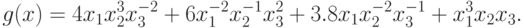
$g(x) = 4 x_{1}x_{2}^{3}x_{3}^{-2} + 6 x_{1}^{-2}x_{2}^{-1}x_{3}^{2} + 3.8 x_{1}x_{2}^{-2}x_{3}^{-1} + x_{1}^{3}x_{2}x_{3}.$

В позином входят три переменные 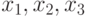x_1, x_2, x_3 . Позином состоит из четырех мономов:

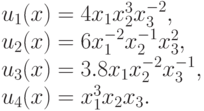
$u_1(x) & = & 4 x_{1}x_{2}^{3}x_{3}^{-2}, \\ u_2(x) & = & 6 x_{1}^{-2}x_{2}^{-1}x_{3}^{2},\\ u_3(x) & = & 3.8 x_{1}x_{2}^{-2}x_{3}^{-1}, \\ u_4(x) & = & x_{1}^{3}x_{2}x_{3}.$

Вектор коэффициентов образован коэффициентами мономов: 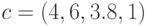c = (4,
6, 3.8, 1) . Матрицей экспонент позинома является ( $4\times 3$ )- матрица

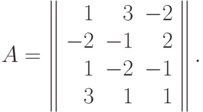
$A=\left\| \begin{array}{rrr} 1 & 3 & -2\\ -2 & -1 & 2 \\ 1 & -2 & -1 \\ 3 & 1 & 1 \end{array} \right\|.$

Вектор коэффициентов позинома и матрица экспонент однозначно определяют позином по формуле (15). Рассмотрим примеры.

Пример 10 По вектору коэффициентов и матрице экспонент

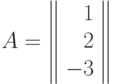
$A=\left\| \begin{array}{r} 1 \\ 2 \\ -3 \end{array} \right\|$

запишем позином в форме (15).

Применяем формулу (16):

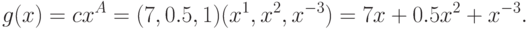
$g(x) = cx^A=(7, 0.5, 1) (x^{1}, x^{2}, x^{-3})=7 x + 0. 5 x^{2} + x^{-3}.$

Пример 11 По вектору коэффициентов и матрице экспонент

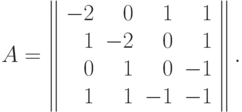
$A=\left\| \begin{array}{rrrr} -2 & 0 & 1 & 1 \\ 1 & -2 & 0 & 1 \\ 0 & 1 & 0 & -1 \\ 1 & 1 & -1 & -1 \end{array} \right\|.$

запишем позином в форме (15).

Применяем формулу (16):

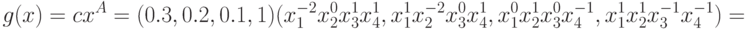
$g(x) = cx^A=(0.3, 0.2, 0.1, 1) (x_{1}^{-2}x_{2}^0x_{3}^1x_{4}^1, % x_{1}^1x_{2}^{-2}x_{3}^0x_{4}^1, x_{1}^0x_{2}^1x_{3}^0x_{4}^{-1}, x_{1}^1x_{2}^1x_{3}^{-1}x_{4}^{-1})=$

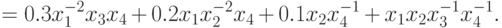
$=0.3 x_{1}^{-2}x_{3}x_{4} + 0.2 x_{1}x_{2}^{-2}x_{4} + 0.1 x_{2}x_{4}^{-1} + x_{1}x_{2}x_{3}^{-1}x_{4}^{-1}.\hphantom{g(x}$

Пример 12 Запишем компоненты позинома из примера 9:

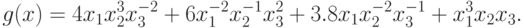
$g(x) = 4 x_{1}x_{2}^{3}x_{3}^{-2} + 6 x_{1}^{-2}x_{2}^{-1}x_{3}^{2} + 3.8 x_{1}x_{2}^{-2}x_{3}^{-1} + x_{1}^{3}x_{2}x_{3}.$

В позином входят три переменные $x_1,\ x_2,\ x_3$ , следовательно, позином состоит из трех компонент. Вектор коэффициентов c= (4, 6, 3.8, 1) . По формуле (17) определяем:

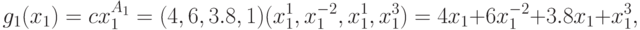
$g_{1}(x_1) = c x_{1}^{A_1} = % (4, 6, 3.8, 1) (x_{1}^{1}, x_{1}^{-2}, x_{1}^{1}, x_{1}^{3}) = 4 x_{1}+6 x_{1}^{-2} + 3.8 x_{1}+x_{1}^{3},$

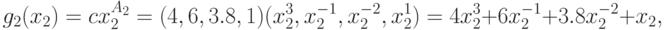
$g_{2}(x_2) = c x_{2}^{A_2} = % (4, 6, 3.8, 1) (x_2^{3}, x_{2}^{-1}, x_{2}^{-2}, x_{2}^{1}) = 4 x_{2}^{3}+6 x_{2}^{-1} + 3.8 x_{2}^{-2} + x_{2},$

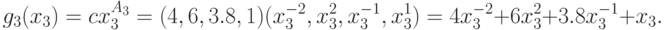
$g_{3}(x_3) = c x_{3}^{A_3} = % (4, 6, 3.8, 1) (x_3^{-2}, x_{3}^{2}, x_{3}^{-1}, x_{3}^{1}) = 4 x_{3}^{-2}+6 x_{3}^{2} + 3.8 x_{3}^{-1}+ x_{3}.$

Следует заметить, что при помощи позиномов описывается большое число закономерностей и отношений, возникающих в различных областях, среди которых: оптимальное планирование, техническое проектирование, исследование химического равновесия, потоки в сетях, оптимальное управление, теория кодирования, управление запасами, системы связи, региональная экономика, автоматизированное проектирование, расчет рисков.

Все задачи оптимизации с позиномами можно разделить на два основных вида: задачи без ограничений, когда минимизируется один позином, и задачи с ограничениями, когда минимизируется некоторый позином, а значения других позиномов не должны превышать единицы. Однако существуют и другие виды задач оптимизации с позиномами. Некоторые из них мы рассмотрим в последующих лекциях.

Краткие итоги

Описаны истоки геометрического программирования, обозначены основные сферы применения. Показана роль неравенства Коши и его обобщения в построении начальной теории. Введены понятия монома и позинома. Перечислены основные свойства множества мономов и множества позиномов. Все определения объяснены на примерах.

Дальше >>

Авторизоваться

Введение в геометрическое программирование

Неравенство Коши и его обобщения

Мономы

Позиномы

Краткие итоги

Вопросы и ответы