Принцип взаимосвязи
Введение
В предыдущих двух лекциях мы рассматривали наши извечные примеры — аукционы первой и второй цены, а также примкнувший к ним неожиданно переставший быть эквивалентным английский аукцион. В тех лекциях мы установили некие соотношения между ожидаемыми доходами участников этих аукционов; а именно, мы установили, что
![\mathbf E\left[R^{\mathrm{Eng}}\right] \ge \mathbf E\left[R^{II}\right] \ge \mathbf E\left[R^I\right].](/sites/default/files/tex_cache/ae509061552223873e03b2b2d2514ba0.png)
Проницательный читатель наверняка давно уже ждет рифмы "розы" и предполагает, что эти соотношения являются лишь частным случаем какого-либо более общего принципа. В этой лекции мы исследуем как раз этот общий принцип, который получил название принцип взаимосвязи (linkage principle). Он предоставляет достаточно легко проверяемое достаточное условие, при помощи которого можно сравнивать разные модели аукционов по их ожидаемому доходу.
Принцип взаимосвязи — изобретение уже довольно давнее (давнее, конечно, если учитывать, насколько молода вообще теория экономических механизмов). Он был доказан в 1982 году Милгромом и Вебером [53]. А вот слегка модифицированный его вариант, который нам потребуется, чтобы классифицировать аукционы, где платит не только победитель, появился на свет совсем недавно; его доказали Кришна и Морган в 1997 году [35,36].
Принцип взаимосвязи
Мы продолжаем рассуждения в том же контексте, что и на предыдущей лекции. Сейчас мы будем выводить общий принцип, поэтому и обозначения чуть обобщим. Для аукциона  обозначим через
обозначим через  его симметричное равновесие. Через
его симметричное равновесие. Через 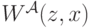 (главное обозначение этой лекции) обозначим ожидаемую цену, которую платит агент
(главное обозначение этой лекции) обозначим ожидаемую цену, которую платит агент  , если он выходит из аукциона победителем, получает сигнал
, если он выходит из аукциона победителем, получает сигнал  и ставит при этом
и ставит при этом  (то есть ставит так, как будто получил
(то есть ставит так, как будто получил 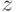 и применил
и применил  ).
).
Пример 11.1. В аукционе первой цены

В аукционе второй цены
![W^{II}(z,x) = \mathbf E\left[\vphantom{1^2}\beta^{II}(Y_1) | X_1 = x, Y_1 < z\right].](/sites/default/files/tex_cache/d278b1fd7dc7c403b0e5df4fb0cb7c87.png)
Конец примера 11.1.
Наконец, через 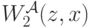 мы обозначим частную производную функции
мы обозначим частную производную функции  по второму аргументу, вычисленную в точке
по второму аргументу, вычисленную в точке  :
:

Соответственно, через 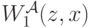 будем обозначать частную производную
будем обозначать частную производную  по первому аргументу в точке
по первому аргументу в точке  .
.
Теперь все готово для того, чтобы сформулировать принцип взаимосвязи.
Теорема 11.1. (принцип взаимосвязи) Пусть  и
и  — два аукциона, в которых побеждает наивысшая ставка и платит только победитель. Пусть в каждом из них есть свое симметричное и возрастающее равновесие, причем:
— два аукциона, в которых побеждает наивысшая ставка и платит только победитель. Пусть в каждом из них есть свое симметричное и возрастающее равновесие, причем:
- для всех
 ;
; - выполняется начальное условие
 .
.
Тогда ожидаемый доход аукциона  не меньше ожидаемого дохода аукциона
не меньше ожидаемого дохода аукциона  .
.
Доказательство. Начнем с аукциона  . Пусть в нем все участники, кроме первого, следуют равновесной стратегии
. Пусть в нем все участники, кроме первого, следуют равновесной стратегии  , а первый ставит
, а первый ставит  . Тогда вероятность его победы составит
. Тогда вероятность его победы составит

Значит, каждый агент в аукционе  максимизирует
максимизирует

Поскольку мы находимся в равновесии, оптимально брать 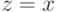 , что дает нам соответствующее условие:
, что дает нам соответствующее условие:

или, что то же самое,

Аналогично,

Значит,

Определим теперь функцию, которая, собственно, показывает, как связаны  и
и  :
:

Тогда
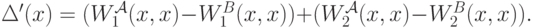
Но первую из этих скобок мы уже знаем, и в итоге получается

Применим теперь условие теоремы. Оно гласит, что
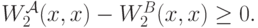
В итоге у нас получилось простенькое дифференциальное уравнение на функцию  вида
вида

где и  , и
, и 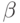 положительные, с начальным условием
положительные, с начальным условием  . Предоставляем читателю убедиться (мы такие уравнения в курсе уже решали), что в решении этого дифференциального уравнения
. Предоставляем читателю убедиться (мы такие уравнения в курсе уже решали), что в решении этого дифференциального уравнения 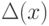 неотрицательна для всех
неотрицательна для всех  , что и требовалось доказать.
, что и требовалось доказать.
Пример 11.2. Принцип взаимосвязи можно применить, например, к сравнению все тех же аукционов. Сравним аукционы первой и второй цены. Мы знаем, что

Это значит, что  для всех
для всех  , потому что функция
, потому что функция 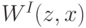 от второго аргумента вообще не зависит. А для аукциона второй цены
от второго аргумента вообще не зависит. А для аукциона второй цены
![W^{II}(z,x) = \mathbf E\left[\beta^{II}(Y_1) | X_1 = x, Y_1 < z\right].](/sites/default/files/tex_cache/92eaf18ca52b3834bb23e386e30d393e.png)
Поскольку  возрастает, то, по аффилированности,
возрастает, то, по аффилированности,  . Значит, доход от аукциона второй цены не меньше дохода от первой цены.
. Значит, доход от аукциона второй цены не меньше дохода от первой цены.
Пример 11.3. А еще принцип взаимосвязи можно ограничить и получить его частный случай — принцип эквивалентности доходности. Если сигналы независимы, то 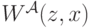 не зависит от
не зависит от  . Значит, в этой ситуации
. Значит, в этой ситуации  для любого аукциона, и доходности у них у всех совпадают.
для любого аукциона, и доходности у них у всех совпадают.
Конец примера 11.3.
