Теоремы Эрроу и Гиббарда-Саттертуэйта
Теорема Гиббарда-Саттертуэйта
В предыдущих лекциях мы уже рассмотрели примеры, в которых были получены правдивые механизмы, успешно реализующие социальную функцию в доминантных стратегиях. Иначе говоря, счастье иногда есть — в некоторых случаях можно построить такой аукцион, в котором агентам вообще не надо ни о чем думать, а результат получается правильный.
Однако теорема Эрроу заставляет задуматься, всегда ли это возможно. К сожалению, ответ совсем не положительный: возможно это далеко не всегда. Теперь мы рассмотрим один из самых больших подвохов всей теории экономических механизмов.
Оказывается, что все-таки не любые механизмы существуют. Сейчас мы сформулируем определение довольно узкого и "нечестного" класса функций социального выбора — так называемых диктаторских функций, которые выгодны ровно одному конкретному участнику (полный аналог диктаторских функций в теореме Эрроу). А потом, как и в теореме Эрроу, докажем, что никаких других реализовать в доминантных стратегиях нельзя.
Этот результат — одна из классических теорем теории экономических механизмов. Она была независимо доказана Аланом Гиббардом и Марком Саттертуэйтом и в их честь и называется [22,74].
Теорема Гиббарда-Саттертуэйта крайне похожа на теорему Эрроу. Она, собственно, из теоремы Эрроу будет следовать (а есть и примеры единого доказательства этих двух результатов [68]). Мы начнем с формулировки того, кто же такие диктаторы в контексте теории экономических механизмов.
Определение 6.7. Функция социального выбора  называется диктаторской, если существует такой агент
называется диктаторской, если существует такой агент  , что для всех возможных векторов типов агентов
, что для всех возможных векторов типов агентов 

Проще говоря, функция социального выбора всегда выбирает один из вариантов, оптимальных для  -го агента.
-го агента.
Вспомним теперь определение 3.9: множеством нижнего контура возможного исхода  при агенте
при агенте  типа
типа  называется множество
называется множество

Это определение позволит нам сформулировать понятие монотонной функции социального выбора.
Определение 6.7. Функция социального выбора  называется монотонной, если для каждого
называется монотонной, если для каждого  и каждого другого
и каждого другого  из того, что для всех
из того, что для всех 

следует, что  .
.
То есть если  , и при переходе к
, и при переходе к  ни у одного агента ни один исход, который раньше был хуже
ни у одного агента ни один исход, который раньше был хуже  , не стал строго лучше
, не стал строго лучше  , то
, то  должен остаться его социальным выбором.
должен остаться его социальным выбором.
Кроме того, важным для нас понятием будут порядки на возможных исходах  , которые для каждого агента задают, что именно ему больше нравится (это те самые порядки предпочтений, которые играли главную роль в доказательствах теоремы Эрроу). Нам не так важно, сколько именно агент получит (конкретное значение
, которые для каждого агента задают, что именно ему больше нравится (это те самые порядки предпочтений, которые играли главную роль в доказательствах теоремы Эрроу). Нам не так важно, сколько именно агент получит (конкретное значение 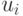 ). Важно то, что он исход
). Важно то, что он исход  ценит выше, чем
ценит выше, чем  , но ниже, чем
, но ниже, чем  . Обозначим через
. Обозначим через  множество всех линейных порядков на
множество всех линейных порядков на  , а через
, а через  — множество порядков, которые может реализовывать агент
— множество порядков, которые может реализовывать агент  .
.
Теперь уже можно сформулировать и доказать основной результат.
Теорема 6.2. (Гиббарда-Саттертуэйта) Предположим, что:
- множество возможных исходов
 конечно и состоит не менее чем из трех элементов:
конечно и состоит не менее чем из трех элементов:  ;
; - все исходы реализуются:
 ;
; - каждый агент может реализовывать любое рациональное множество предпочтений:
 .
.
Тогда функция социального выбора  правдиво реализуема в доминантных стратегиях тогда и только тогда, когда она диктаторская.
правдиво реализуема в доминантных стратегиях тогда и только тогда, когда она диктаторская.
Доказательство. Доказательство следствия справа налево тривиально: совершенно очевидно, что диктаторская  правдиво реализуема в доминантных стратегиях. Нужно просто выбирать исход, оптимальный для агента-диктатора, и не обращать внимания на других. При этом для диктатора правдивая стратегия будет, безусловно, доминантной, а другие агенты вообще не влияют на исход, поэтому для них правдивая стратегия не лучше и не хуже любой другой. Дальше мы будем доказывать следствие слева направо.
правдиво реализуема в доминантных стратегиях. Нужно просто выбирать исход, оптимальный для агента-диктатора, и не обращать внимания на других. При этом для диктатора правдивая стратегия будет, безусловно, доминантной, а другие агенты вообще не влияют на исход, поэтому для них правдивая стратегия не лучше и не хуже любой другой. Дальше мы будем доказывать следствие слева направо.
Доказывать будем в три приема, тремя леммами.
Лемма 6.2. Если  для всех
для всех  , и
, и  правдиво реализуема в доминантных стратегиях, то
правдиво реализуема в доминантных стратегиях, то  монотонна.
монотонна.
Доказательство. Рассмотрим два профиля типов  и
и  , для которых
, для которых

Мы хотим показать, что  .
.
Доказательство будет следовать классической схеме: взять один вектор (профиль типов) и менять его покомпонентно, пока он не станет совпадать со вторым. Поскольку  правдиво реализуема, то
правдиво реализуема, то

и, с другой стороны,  . Так как порядки линейные, и все сравнимо (это то же самое условие, которое в теореме Эрроу называлось "строгими предпочтениями"), из этого следует, что
. Так как порядки линейные, и все сравнимо (это то же самое условие, которое в теореме Эрроу называлось "строгими предпочтениями"), из этого следует, что

Теперь можно доказать, что

И так далее, и тому подобное. В общем,  .
.
Лемма 6.3. Если  для всех
для всех  ,
,  монотонна, и
монотонна, и  , то
, то  эффективна ex post.
эффективна ex post.
Доказательство. Если  для всех
для всех  ,
,  монотонна и
монотонна и  , то
, то  эффективна ex post. Напомним, что "эффективна ex post" означает, что уже после того, как агенты сыграют по своим стратегиям, для каждого возможного значения
эффективна ex post. Напомним, что "эффективна ex post" означает, что уже после того, как агенты сыграют по своим стратегиям, для каждого возможного значения  нельзя сместить равновесие туда, где всем будет лучше.
нельзя сместить равновесие туда, где всем будет лучше.
Предположим противное. Пусть существуют такие 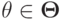 и
и  , что
, что

(равенство невозможно, потому что нет несравнимых исходов). Воспользуемся тем, что  (сюръективностью). Это значит, что есть такой
(сюръективностью). Это значит, что есть такой  , что
, что  .
.
А теперь воспользуемся тем, что все предпочтения в  возможны. Выберем такой вектор
возможны. Выберем такой вектор  , что
, что

Поскольку

для всех  , то, по монотонности,
, то, по монотонности,  . А это приводит к противоречию, так как
. А это приводит к противоречию, так как  .
.
Итак, теперь мы все подготовили к тому, чтобы напрямую применить теорему Эрроу.
Лемма 6.4. Если  монотонна и эффективна ex post, то она диктаторская.
монотонна и эффективна ex post, то она диктаторская.
Доказательство. Эта лемма является прямым следствием из теоремы Эрроу о невозможности (теоремы 6.1).
Суммарно эти три леммы и доказывают теорему Гиббарда-Саттертуэйта.
