Обработки результатов измерений с многократными наблюдениями
Обработки результатов измерений с многократными наблюдениями
Наиболее часто инструментальное энергетическое обследования предполагает проведение прямых измерений с многократными наблюдениями, т.к. это позволяет существенно повысить достоверность результатов даже при влиянии помех различной физической природы и нестабильности режимов работы оборудования. Остановимся на методике их проведения и обработке результатов, которая имеет целый ряд особенностей [ 6.1 ] .
Исходным материалом для прямых измерений с многократными наблюдениями является массив результатов наблюдений, т.е., например, массив показаний того или иного измерительного прибора. Дальнейшая последовательность операций следующая:
показаний того или иного измерительного прибора. Дальнейшая последовательность операций следующая:
- Из массива результатов наблюдений исключаются известные систематические погрешности, т.е. погрешности либо постоянные во времени или изменяющиеся по детерминированным законам.
- Элементы массива располагаются в порядке возрастания их значений от
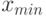 до
до с целью выявления промахов (грубых погрешностей).
с целью выявления промахов (грубых погрешностей). -
Обнаруживаются и исключаются промахи..
Признаком промаха в наблюдения является его значительное удаление от центра распределения. Для принятия решения об исключении предполагаемого промаха необходимы формальные критерии. В общем случае границы выборки для удаления промахов определяются видом функции распределения случайных погрешностей и объемом n выборки [ 6.2 ] . При проведении инструментального энергетического обследования рекомендуется применить упрощенный метод обнаружения промахов, используя критерий:

где
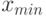 и
и – соответственно, самое большое и наименьшее значения в исходных данных;
– соответственно, самое большое и наименьшее значения в исходных данных; - среднее арифметическое значение измеряемой величины;
- среднее арифметическое значение измеряемой величины; - среднее квадратическое отклонение.
- среднее квадратическое отклонение.Полученное значение К сравнивают с табличным значением
 . Если
. Если , то
, то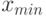 или
или можно отбросить при заданном уровне значимости
можно отбросить при заданном уровне значимости . Значение доверительной вероятности Р для технических измерений принять равным
. Значение доверительной вероятности Р для технических измерений принять равным , тогда
, тогда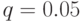 .
.В таблица 6.1 приведены значения
 при различном числе наблюдений n при уровне значимости 0,95.
при различном числе наблюдений n при уровне значимости 0,95. - Вычисляется среднее арифметическое исправленных результатов наблюдений:
Полученное значение принимается за результат измерения.
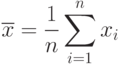
- Вычисляется оценка среднего квадратического отклонения результатов наблюдений:

- Рассчитывается оценка среднего квадратического отклонения результата измерения (среднего арифметического):

- Проверяется принадлежность распределения результатов наблюдений нормальному закону распределения.
Обычно при проведении инструментального энергетического обследования число наблюдений лежит в диапазоне
 . В этом случае нормальность распределения проверяется при помощи вычисления составного критерия и сравнения его значения с табличным. Для этого вычисляют отношение
. В этом случае нормальность распределения проверяется при помощи вычисления составного критерия и сравнения его значения с табличным. Для этого вычисляют отношение по формуле:
где
по формуле:
где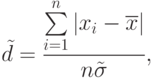
 - смещенная оценка СКО, вычисленная по формуле
Гипотеза о нормальности распределения по составному критерию не отвергается, если
- смещенная оценка СКО, вычисленная по формуле
Гипотеза о нормальности распределения по составному критерию не отвергается, если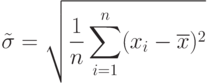

Значения квантилей распределения для выбранных уровней значимости приведены в таблица 6.2
Таблица 6.2. n 
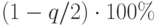
1% 5% 96% 99% 16 0.9137 0.8884 0.7236 0.6829 21 0.9001 0.8768 0.7304 0.6950 26 0.8901 0.8686 0.7360 0.7040 31 0.8826 0.8625 0.7404 0.7110 36 0.8769 0.8578 0.7440 0.7167 41 0.8722 0.8540 0.7470 0.7216 47 0.8682 0.8508 0.7496 0.7256 51 0.8648 0.8481 0.7518 0.7291 При числе наблюдений n>50 для проверки принадлежности их к нормальному распределению применить критерий Пирсона X2 по указаниям, приведенным в [ 6.3 ] .
- Определяют доверительные границы
 случайной составляющей погрешности результата измерений по формуле
[
6.4
]
:
случайной составляющей погрешности результата измерений по формуле
[
6.4
]
:

где t - коэффициент Стьюдента, значение которого зависит от доверительной вероятности Р и числа наблюдений и приведены в таблица 6.3
- Вычисляют границы
 неисключенной систематической погрешности метода, средства измерения и вызванные влияющими факторами.
неисключенной систематической погрешности метода, средства измерения и вызванные влияющими факторами.
Значения
 погрешностей задаются преподавателем, предполагается, что законы распределения неисключенной погрешности неизвестны. Так как каждая из составляющих систематической погрешности имеет свой доверительный интервал (границы), то границы суммарной погрешности находят по формуле:где m - число не исключенных систематических составляющих погрешности; K - коэффициент, определяемый значением доверительной вероятности, при
погрешностей задаются преподавателем, предполагается, что законы распределения неисключенной погрешности неизвестны. Так как каждая из составляющих систематической погрешности имеет свой доверительный интервал (границы), то границы суммарной погрешности находят по формуле:где m - число не исключенных систематических составляющих погрешности; K - коэффициент, определяемый значением доверительной вероятности, при
 , коэффициент
, коэффициент 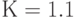 .
.
- Определяют соотношение между не исключенной систематической погрешностью, и средним квадратическим отклонением результата измерения
 .
.
Если отношение
 меньше 0.8, то неисключеными систематическими погрешностями пренебрегают и в качестве границы погрешности принимают результат
меньше 0.8, то неисключеными систематическими погрешностями пренебрегают и в качестве границы погрешности принимают результат . Если же результат
. Если же результат больше 8, то пренебрегают случайной погрешностью и считают границу погрешности результата
больше 8, то пренебрегают случайной погрешностью и считают границу погрешности результата  . В случае, когда результат вычислений лежит в интервале
. В случае, когда результат вычислений лежит в интервале , то определение границ погрешности результата измерения
, то определение границ погрешности результата измерения производятся с учетом случайной и систематической составляющих погрешности по формуле:
производятся с учетом случайной и систематической составляющих погрешности по формуле:
где К - коэффициент, зависящий от соотношения случайной и не исключенной систематической погрешностей и определяется по формуле:
Оценка суммарного СКО результата измерения, вычисляется по формуле:
где К - коэффициент, зависящий от соотношения случайной и не исключенной систематической погрешностей и определяется по формуле:

Оценка суммарного СКО результата измерения , вычисляется по формуле:

- Производится запись результата измерения с учётом следующего. Наименьшие разряды числовых значений результата измерения должны быть такими же, как наименьшие разряды числовых значений СКО абсолютной погрешности измерения или значений границ, в которых находится абсолютная погрешность. Например, запись результата измерения активной электрической мощности, выполненная по аттестованной методике выполнения измерений
[
6.5
]
, имеет следующий вид:
Результат измерения:

Ключевые термины:
Массив результатов наблюденийисходный материал для прямых измерений с многократными наблюдениями является, т.е., например, массив показаний того или иного измерительного прибора.
показаний того или иного измерительного прибора.
Систематические погрешности– погрешности либо постоянные во времени или изменяющиеся по детерминированным законам.
Промахи– грубые погрешности, признаком которых является их значительное удаление от центра распределения массива результатов наблюдений.
Среднее арифметическое значение измеряемой величины оценка математического ожидания.
Краткие итоги лекции:
- Наиболее часто инструментальное энергетическое обследования предполагает проведение прямых измерений с многократными наблюдениями, т.к. это позволяет существенно повысить достоверность результатов даже при влиянии помех различной физической природы и нестабильности режимов работы оборудования.
- Исходным материалом для прямых измерений с многократными наблюдениями является массив результатов наблюдений, т.е., например, массив
 показаний того или иного измерительного прибора.
показаний того или иного измерительного прибора. - Обычно при проведении инструментального энергетического обследования число наблюдений лежит в диапазоне
 . В этом случае нормальность распределения проверяется при помощи вычисления составного критерия и сравнения его значения с табличным.
. В этом случае нормальность распределения проверяется при помощи вычисления составного критерия и сравнения его значения с табличным.
