|
поддерживаю выше заданые вопросы
|
Умножение разреженных матриц
Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного варианта метода верхней релаксации проводились при условиях, указанных во введении. С целью формирования симметричной положительно определенной матрицы элементы подматрицы  генерировались в диапа-зоне от 0 до 1, значения элементов подматрицы
генерировались в диапа-зоне от 0 до 1, значения элементов подматрицы  получались из симметрии матриц
получались из симметрии матриц  и
и  , а элементы на главной диагонали (подматрица
, а элементы на главной диагонали (подматрица  ) генерировались в диапазоне от
) генерировались в диапазоне от  до
до  , где
, где  – размер матрицы.
– размер матрицы.
В качестве критерия остановки использовался критерий остановки по точности (7.51) с параметром 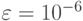 а итерационный параметр
а итерационный параметр  . Во всех экспериментах метод нашел решение с требуемой точностью за 11 итераций. Как и для предыдущих экспериментов, ускорение будем фиксировать по сравнению с параллельной программой, запущенной в один поток.
. Во всех экспериментах метод нашел решение с требуемой точностью за 11 итераций. Как и для предыдущих экспериментов, ускорение будем фиксировать по сравнению с параллельной программой, запущенной в один поток.
| n | 1 поток | Параллельный алгоритм | |||||||
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| T | S | T | S | T | S | T | S | ||
| 2500 | 0,73 | 0,47 | 1,57 | 0,30 | 2,48 | 0,25 | 2,93 | 0,22 | 3,35 |
| 5000 | 3,25 | 2,11 | 1,54 | 1,22 | 2,67 | 0,98 | 3,30 | 0,80 | 4,08 |
| 7500 | 7,72 | 5,05 | 1,53 | 3,18 | 2,43 | 2,36 | 3,28 | 1,84 | 4,19 |
| 10000 | 14,60 | 9,77 | 1,50 | 5,94 | 2,46 | 4,52 | 3,23 | 3,56 | 4,10 |
| 12500 | 25,54 | 17,63 | 1,45 | 10,44 | 2,45 | 7,35 | 3,48 | 5,79 | 4,41 |
| 15000 | 38,64 | 26,36 | 1,47 | 15,32 | 2,52 | 10,84 | 3,56 | 8,50 | 4,54 |
Эксперименты демонстрируют неплохое ускорение (порядка 4 на 8-и потоках).
Метод сопряженных градиентов
Рассмотрим систему линейных уравнений (7.49) с симметричной, положительно определенной матрицей  размера
размера  . Основой метода
сопряженных градиентов является следующее свойство: решение системы линейных уравнений (7.49) с симметричной положительно определенной матрицей
. Основой метода
сопряженных градиентов является следующее свойство: решение системы линейных уравнений (7.49) с симметричной положительно определенной матрицей  эквивалентно решению задачи минимизации функции
эквивалентно решению задачи минимизации функции
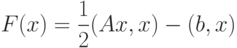 |
( 7.56) |
 . В самом деле, функция
. В самом деле, функция  достигает своего минимального значения тогда и только тогда, когда ее градиент
достигает своего минимального значения тогда и только тогда, когда ее градиент 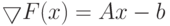 |
( 7.57) |
Последовательный алгоритм
С целью решения задачи минимизации (7.56) организуется следующий итерационный процесс.
Подготовительный шаг ( ) определяется формулами
) определяется формулами

 – произвольное начальное приближение; а коэффициент
– произвольное начальное приближение; а коэффициент 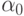 вычисляется как
вычисляется как 
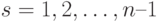

 – невязка
– невязка  -го приближения, коэффициент
-го приближения, коэффициент  находят
из условия сопряженности
находят
из условия сопряженности 
 и
и  ;
; 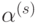 является решением задачи минимизации
функции
является решением задачи минимизации
функции  по направлению
по направлению 

Анализ расчетных формул метода показывает, что они включают две операции умножения матрицы на вектор, четыре операции скалярного произведения и пять операций над векторами. Однако на каждой итерации произведение 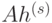 достаточно вычислить один раз, а затем использовать сохраненный результат. Общее количество числа операций, выполняемых на
одной итерации, составляет
достаточно вычислить один раз, а затем использовать сохраненный результат. Общее количество числа операций, выполняемых на
одной итерации, составляет
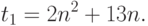
Таким образом, выполнение  итераций метода потребует
итераций метода потребует
 |
( 7.58) |
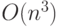 . Однако ввиду ошибок округления данный процесс обычно рассматривают как итераци-
онный, процесс завершается либо при выполнении обычного условия остановки (7.51) , либо при выполнении условия малости относительной нормы
невязки
. Однако ввиду ошибок округления данный процесс обычно рассматривают как итераци-
онный, процесс завершается либо при выполнении обычного условия остановки (7.51) , либо при выполнении условия малости относительной нормы
невязки 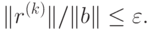
Организация параллельных вычислений
При разработке параллельного варианта метода сопряженных градиентов для решения систем линейных уравнений в первую очередь следует учесть, что выполнение итераций метода осуществляется последовательно и, тем самым, наиболее целесообразный подход состоит в распараллеливании вычислений, реализуемых в ходе выполнения итераций.
Анализ последовательного алгоритма показывает, что основные затраты на
 -й итерации состоят в умножении матрицы
-й итерации состоят в умножении матрицы  на вектора
на вектора  и
и  . Как ре-
зультат, при организации параллельных вычислений могут быть использованы известные методы параллельного умножения матрицы на вектор.
. Как ре-
зультат, при организации параллельных вычислений могут быть использованы известные методы параллельного умножения матрицы на вектор.
Дополнительные вычисления, имеющие меньший порядок сложности, представляют собой различные операции обработки векторов (скалярное произведение, сложение и вычитание, умножение на скаляр). Организация таких вычислений, конечно же, должна быть согласована с выбранным параллельным способом выполнения операция умножения матрицы на вектор.
Выберем для дальнейшего анализа эффективности получаемых параллельных вычислений параллельный алгоритм матрично-векторного умножения при ленточном горизонтальном разделении матрицы. При этом операции над векторами, обладающие меньшей вычислительной трудоемкостью, также будем выполнять в многопоточном режиме.
Вычислительная трудоемкость последовательного метода сопряженных градиентов определяется соотношением (7.58). Определим время выполнения параллельной реализации метода сопряженных градиентов. Вычислительная сложность параллельной операции умножения матрицы на вектор при использовании схемы ленточного горизонтального разделения матрицы составляет

 – длина вектора,
– длина вектора,  – число потоков,
– число потоков, 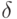 – накладные расходы на созда-
ние и закрытие параллельной секции.
– накладные расходы на созда-
ние и закрытие параллельной секции.Все остальные операции над векторами (скалярное произведение, сложение, умножение на константу) могут быть выполнены в однопоточном режиме, т.к. не являются определяющими в общей трудоемкости метода. Следовательно, общая вычислительная сложность параллельного варианта метода сопряженных градиентов может быть оценена как

 – число итераций метода.
– число итераций метода.Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного
варианта метода сопряженных градиентов для решения систем линейных
уравнений с симметричной положительно определенной матрицей прово-
дились при условиях, указанных во введении. Элементы на главной диагонали матрицы  ) генерировались в диапазоне от
) генерировались в диапазоне от  до
до  , где
, где  – размер
матрицы, остальные элементы генерировались симметрично в диапазоне от
0 до 1. В качестве критерия остановки использовался критерий остановки
по точности (7.51) с параметром
– размер
матрицы, остальные элементы генерировались симметрично в диапазоне от
0 до 1. В качестве критерия остановки использовался критерий остановки
по точности (7.51) с параметром
Результаты вычислительных экспериментов приведены в таблице 7.21(время работы алгоритмов указано в секундах).
| n | 1 поток | Параллельный алгоритм | |||||||
| 2 потока | 4 потока | 6 потоков | 8 потоков | ||||||
| T | S | T | S | T | S | T | S | ||
| 500 | 0,02 | 0,01 | 1,64 | 0,01 | 2,56 | 0,01 | 2,56 | 0,01 | 2,56 |
| 1000 | 0,21 | 0,16 | 1,26 | 0,10 | 2,09 | 0,07 | 2,88 | 0,05 | 3,83 |
| 1500 | 0,65 | 0,48 | 1,36 | 0,27 | 2,41 | 0,19 | 3,42 | 0,15 | 4,20 |
| 2000 | 1,32 | 0,94 | 1,41 | 0,53 | 2,51 | 0,38 | 3,48 | 0,29 | 4,50 |
| 3000 | 3,42 | 2,34 | 1,46 | 1,33 | 2,58 | 0,96 | 3,56 | 0,74 | 4,63 |
| 4000 | 6,49 | 4,54 | 1,43 | 2,53 | 2,56 | 1,80 | 3,60 | 1,40 | 4,62 |
| 5000 | 11,02 | 7,41 | 1,49 | 4,17 | 2,65 | 2,98 | 3,70 | 2,31 | 4,78 |
Так как операция умножения матрицы на вектор – основная по трудоемкости операция на одной итерации метода – распараллеливается хорошо, то и эффективность распараллеливания метода сопряженных градиентов будет линейная, что подтверждается приведенным графиком.
Спад ускорения при  объясняется недостаточной вычислительной нагрузкой, которая приходится на каждый процесс (этот эффект будет проиллюстрирован и в дальнейшем при решении дифференциальных уравнений в частных производных). Использовать более чем 4 потока для решения данной задачи при
объясняется недостаточной вычислительной нагрузкой, которая приходится на каждый процесс (этот эффект будет проиллюстрирован и в дальнейшем при решении дифференциальных уравнений в частных производных). Использовать более чем 4 потока для решения данной задачи при  – нецелесообразно.
– нецелесообразно.



