Reversi
How the Code Works
The Game Board Data Structure
Before we get into the code, we should talk about the board data structure. This data structure is a list of lists, just like the one in our previous Sonar game. The list is created so that board[x][y] will represent the character on space located at position x on the X-axis (going left/right) and position y on the Y-axis (going up/down). This character can either be a ' ' space character (to represent a blank space), a '.' period character (to represent a possible move in hint mode), or an 'X' or 'O' (to represent a player's tile). Whenever you see a parameter named board, that parameter variable is meant to be this list of lists board data structure.
Importing Other Modules
1. # Reversi 2. 3. import random 4. import sys
We import the random module for its randint() and choice() functions and sys module for its exit() function.
Drawing the Board Data Structure on the Screen
6. def drawBoard(board):
7. # This function prints out the board that it was passed. Returns None.
8. HLINE = ' +---+---+---+---+---+---+---+---+'
9. VLINE = ' | | | | | | | | | '
10.
11. print(' 1 2 3 4 5 6 7 8')
12. print(HLINE)
The drawBoard() function will print out the current game board based on the structure in board. Notice that each square of the board looks like this:
+---+ | | | X | | | +---+ !
Since we are going to print the string with the horizontal line (and plus signs at the intersections) over and over again, we will store that in a constant variable named HLI There are also lines above and below the very center of X or O tile that are nothing bu characters (called "pipe" characters) with three spaces in between. We will store this s in a constant named VLINE.
Line 11 is the first print() function call executed, and it prints out the labels for X-axis along the top of the board. Line 12 prints the top horizontal line of the board.
13. for y in range(8):
14. print(VLINE)
15. print(y+1, end=' ')
16. for x in range(8):
17. print('| %s' % (board[x] [y]), end=' ')
18. print('|')
19. print(VLINE)
20. print(HLINE)
Printing each row of spaces on the board is fairly repetitive, so we can use a loop here. W will loop eight times, once for each row. Line 15 prints the label for the Y-axis on the left side of the board, and has a comma at the end of it to prevent a new line. This is so we can have another loop (which again loops eight times, once for each space) print out each space (along with the 'X', 'O', or ' ' character for that space depending on what is stored in board.
The print() function call inside the inner loop also has a comma at the end of it, meaning a space character is printed instead of a newline character. This produces the second space in the pipe-space-tile-space string that we print out, over and over for eight times. That will produce a single line on the screen that looks like '| X | X | X | X | X | X | X | X ' (that is, if each of the board[x][y] values were 'X'). After t inner loop is done, the print() function call on line 18 prints out the final '|' character along with a newline (since it does not end with a comma).
(The print() call forces us to always print a newline character or a space at the end of everything we print. If we do not want this last character, then we can always use the sys.stdout.write() function, which has a single string parameter that it prints out. B sure to import sys first before calling this function.)
The code inside the outer for loop that begins on line 13 prints out an entire row of the board like this:
| | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+
When printed out eight times, it forms the entire board (of course, some of the spaces on the board will have 'O' or ' ' instead of 'X'.:
| | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+ | | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+ | | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+ | | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+ | | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+ | | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+ | | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+ | | | | | | | | | | X | X | X | X | X | X | X | X | | | | | | | | | | +---+---+---+---+---+---+---+---+
Resetting the Game Board
An important thing to remember is that the coordinates that we print out to the player are from 1 to 8, but the indexes in the board data structure are from 0 to 7.
23. def resetBoard(board): 24. # Blanks out the board it is passed, except for the original starting position. 25. for x in range(8): 26. for y in range(8): 27. board[x] [y] = ' '
Here we use a loop inside a loop to set the board data structure to be all blanks. We will call the resetBoard() function whenever we start a new game and want to remove the tiles from a previous game.
Setting Up the Starting Pieces
29. # Starting pieces: 30. board[3] [3] = 'X' 31. board[3] [4] = 'O' 32. board[4] [3] = 'O' 33. board[4] [4] = 'X'
When we start a new game of Reversi, it isn't enough to have a completely blank board. At the very beginning, each player has two tiles already laid down in the very center, so we will also have to set those.
We do not have to return the board variable, because board is a reference to a list. Even when we make changes inside the local function's scope, these changes happen in the global scope to the list that was passed as an argument. (Remember, this is one way list variables are different from non-list variables.)
Creating a New Game Board Data Structure
36. def getNewBoard(): 37. # Creates a brand new, blank board data structure. 38. board = [] 39. for i in range(8): 40. board.append([' '] * 8) 41. 42. return board
The getNewBoard() function creates a new board data structure and returns it. Line 38 creates the outer list and assigns a reference to this list to board. Line 40 create the inner lists using list replication. ( [' '] * 8 is the same as [' ', ' ', ' ', ' ', ' ', ' ', ' ', ' '] but with less typing.) The for loop here runs line 40 eight times to create the eight inner lists. The spaces represent a completely empty game board.
Checking if a Move is Valid
45. def isValidMove(board, tile, xstart, ystart): 46. # Returns False if the player's move on space xstart, ystart is invalid. 47. # If it is a valid move, returns a list of spaces that would become the player's if they made a move here. 48. if board[xstart] [ystart] != ' ' or not isOnBoard (xstart, ystart): 49. return False 50 . 51. board[xstart] [ystart] = tile # temporarily set the tile on the board. 52 . 53 . if tile == 'X' : 54. otherTile = 'O' 55. else: 56. otherTile = 'X' 57. 58. tilesToFlip = []
isValidMove() is one of the more complicated functions. Given a board data structure, the player's tile, and the XY coordinates for player's move, this function should return True if the Reversi game rules allow that move and False if they don't.
The easiest check we can do to disqualify a move is to see if the XY coordinates are on the game board or if the space at XY is not empty. This is what the if statement on line 48 checks for. isOnBoard() is a function we will write that makes sure both the X and Y coordinates are between 0 and 7.
For the purposes of this function, we will go ahead and mark the XY coordinate pointed to by xstart and ystart with the player's tile. We set this place on the board back to a space before we leave this function.
The player's tile has been passed to us, but we will need to be able to identify the other player's tile. If the player's tile is 'X' then obviously the other player's tile is 'O'. And it is the same the other way.
Finally, if the given XY coordinate ends up as a valid position, we will return a list of all the opponent's tiles that would be flipped by this move.
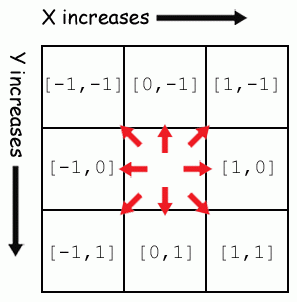
59. for xdirection, ydirection in [[0, 1], [1, 1], [1, 0], [1, -1] ,
[0, -1] , [-1, -1] , [-1, 0], [-1, 1] ] :
The for loop iterates through a list of lists which represent directions you can move on the game board. The game board is a Cartesian coordinate system with an X and Y direction. There are eight directions you can move: up, down, left, right, and the four diagonal directions. We will move around the board in a direction by adding the first value in the two-item list to our X coordinate, and the second value to our Y coordinate.
Because the X coordinates increase as you go to the right, you can "move" to the right by adding 1 to the X coordinate. Moving to the left is the opposite: you would subtract 1 (or add -1) from the X coordinate. We can move up, down, left, and right by adding or subtracting to only one coordinate at a time. But to move diagonally, we need to add or subtract to both coordinates. For example, adding 1 to the X coordinate to move right and adding -1 to the Y coordinate to move up would result in moving to the up-right diagonal direction.
Checking Each of the Eight Directions
Here is a diagram to make it easier to remember which two-item list represents which direction:
59. for xdirection, ydirection in [[0, 1] , [1, 1] , [1, 0],
[1, -1] , [0, -1] , [-1, -1] , [-1, 0], [-1, 1] ] :
60. x, y = xstart, ystart
61. x += xdirection # first step in the direction
62. y += ydirection # first step in the direction
Line 60 sets an x and y variable to be the same value as xstart and ystart, respectively. We will change x and y to "move" in the direction that xdirection and ydirection dictate. xstart and ystart will stay the same so we can remember which space we originally intended to check. (Remember, we need to set this place back to a space character, so we shouldn't overwrite the values in them.)
We make the first step in the direction as the first part of our algorithm.
63. if isOnBoard(x, y) and board[x] [y] == otherTile: 64. # There is a piece belonging to the other player next to our piece. 65. x += xdirection 66. y += ydirection 67. if not isOnBoard(x, y): 68. continue
Remember, in order for this to be a valid move, the first step in this direction must be 1) on the board and 2) must be occupied by the other player's tile. Otherwise there is no chance to flip over any of the opponent's tiles. In that case, the if statement on line 63 is not True and execution goes back to the for statement for the next direction.
But if the first space does have the other player's tile, then we should keep proceeding in that direction until we reach on of our own tiles. If we move off of the board, then we should continue back to the for statement to try the next direction.
69. while board[x] [y] == otherTile: 70. x += xdirection 71. y += ydirection 72. if not isOnBoard(x, y): # break out of while oop, then continue in for loop 73. break 74. if not isOnBoard(x, y): 75. continue
The while loop on line 69 ensures that x and y keep going in the current direction as long as we keep seeing a trail of the other player's tiles. If x and y move off of the board, we break out of the for loop and the flow of execution moves to line 74. What we really want to do is break out of the while loop but continue in the for loop. But if we put a continue statement on line 73, that would only continue to the while loop on line 69.
Instead, we recheck not isOnBoard(x, y) on line 74 and then continue from there, which goes to the next direction in the for statement. It is important to know that break and continue will only break or continue in the loop they are called from, and not an outer loop that contain the loop they are called from.
Finding Out if There are Pieces to Flip Over
76. if board[x] [y] == tile: 77. # There are pieces to flip over. Go in the reverse direction until we reach the original space, noting all the tiles along the way. 78. while True: 79. x -= xdirection 80. y -= ydirection 81. if x == xstart and y == ystart: 82. break 83. tilesToFlip.append([x, y])
If the while loop on line 69 stopped looping because the condition was False, then we have found a space on the board that holds our own tile or a blank space. Line 76 checks if this space on the board holds one of our tiles. If it does, then we have found a valid move. We start a new while loop, this time subtracting x and y to move them in the opposite direction they were originally going. We note each space between our tiles on the board by appending the space to the tilesToFlip list.
We break out of the while loop once x and y have returned to the original position (which was still stored in xstart and ystart).
85. board[xstart] [ystart] = ' ' # restore the empty space 86. if len(tilesToFlip) == 0: # If no tiles were flipped, this is not a valid move. 87. return False 88. return tilesToFlip
We perform this check in all eight directions, and afterwards the tilesToFlip list will contain the XY coordinates all of our opponent's tiles that would be flipped if the player moved on xstart, ystart. Remember, the isValidMove() function is only checking to see if the original move was valid, it does not actually change the data structure of the game board.
If none of the eight directions ended up flipping at least one of the opponent's tiles, then tilesToFlip would be an empty list and this move would not be valid. In that case, isValidMove() should return False. Otherwise, we should return tilesToFlip.
Checking for Valid Coordinates
91. def isOnBoard(x, y): 92. # Returns True if the coordinates are located on the board. 93. return x >= 0 and x <= 7 and y >= 0 and y <=7
isOnBoard() is a function called from isValidMove(), and is just shorthand for the rather complicated Boolean expression that returns True if both x and y are in between 0 and 7. This function lets us make sure that the coordinates are actually on the game board.
Getting a List with All Valid Moves
96. def getBoardWithValidMoves(board, tile) : 97. # Returns a new board with . marking the valid moves the given player can make. 98. dupeBoard = getBoardCopy(board) 99 . 100. for x, y in getValidMoves(dupeBoard, tile) : 101. dupeBoard[x] [y] = '.' 102. return dupeBoard
getBoardWithValidMoves() is used to return a game board data structure that has '.' characters for all valid moves on the board. This is used by the hints mode to display to the player a board with all possible moves marked on it.
Notice that this function creates a duplicate game board data structure instead of modifying the one passed to it by the board parameter. Line 100 calls getValidMoves(), which returns a list of xy coordinates with all the legal moves the player could make. The board copy is then marked with a period in those spaces. How getValidMoves() works is described next.
105. def getValidMoves(board, tile): 106. # Returns a list of [x,y] lists of valid moves for the given player on the given board. 107. validMoves = [] 108 . 109. for x in range(8) : 110. for y in range(8): 111. if isValidMove(board, tile, x, y) != False: 112. validMoves.append([x, y]) 113. return validMoves
The getValidMoves() function returns a list of two-item lists that hold the XY coordinates for all valid moves for tile's player, given a particular game board data structure in board.
This function uses two loops to check every single XY coordinate (all sixty four of them) by calling isValidMove() on that space and checking if it returns False or a list of possible moves (in which case it is a valid move). Each valid XY coordinate is appended to the list, validMoves.