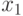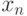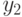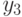|
Возможна ли разработка приложения на Octave с GUI? |
Обработка результатов эксперимента. Метод наименьших квадратов
11.1 Постановка задачи
Метод наименьших квадратов (МНК) позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно.
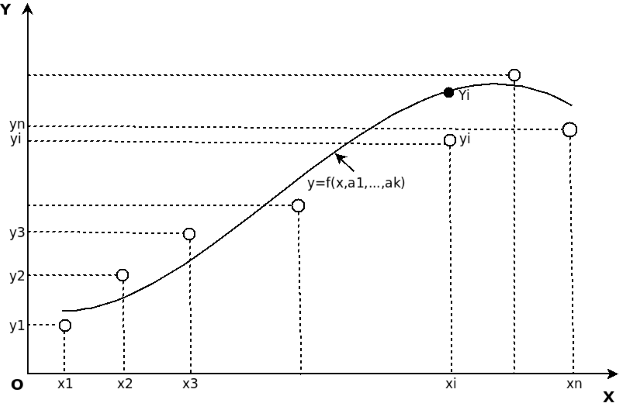
В общем случае задачу можно сформулировать следующим образом. Пусть в результате эксперимента были получены некая экспериментальная зависимость 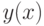 , представленная в таблице 11.1. Необходимо построить аналитическую зависимость
, представленная в таблице 11.1. Необходимо построить аналитическую зависимость 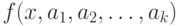 , наиболее точно описывающую результаты эксперимента. Для построения параметров функции
, наиболее точно описывающую результаты эксперимента. Для построения параметров функции 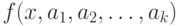 будем использовать метод наименьших квадратов. Идея метода наименьших квадратов заключается в том, что функцию
будем использовать метод наименьших квадратов. Идея метода наименьших квадратов заключается в том, что функцию 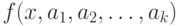 необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений
необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений  была бы наименьшей (см. рис. 11.1):
была бы наименьшей (см. рис. 11.1):
 |
( 11.1) |
Задача состоит из двух этапов:
- По результатам эксперимента определить внешний вид подбираемой зависимости.
- Подобрать коэффициенты зависимости
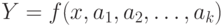 .
.
Математически задача подбора коэффициентов зависимости сводится к определению коэффициентов  из условия (11.1). В Octave её можно решать несколькими способами:
из условия (11.1). В Octave её можно решать несколькими способами:
- Решать как задачу поиска минимума функции многих переменных без ограничений с использованием функции
 .
. - Использовать специализированную функцию
 .
. - Используя аппарат высшей математики, составить и решить систему алгебраических уравнений для определения коэффициентов
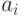 .
.
11.2 Подбор параметров экспериментальной зависимости методом наименьших квадратов
Вспомним некоторые сведения из высшей математики, необходимые для решения задачи подбора зависимости методом наименьших квадратов.
Достаточным условием минимума функции 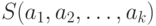 является равенство нулю всех её частных производных. Поэтому задача поиска минимума функции (11.1) эквивалентна решению системы
является равенство нулю всех её частных производных. Поэтому задача поиска минимума функции (11.1) эквивалентна решению системы
алгебраических уравнений:
 |
( 11.2) |
Если параметры 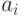 входят в зависимость
входят в зависимость 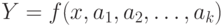 линейно, то получим систему (11.3) из k линейных уравнений с
линейно, то получим систему (11.3) из k линейных уравнений с  неизвестными.
неизвестными.
 |
( 11.3) |
Составим систему (11.3) для наиболее часто используемых функций.