|
Возможна ли разработка приложения на Octave с GUI? |
Решение оптимизационных задач
10.2 Решение задач линейного программирования
Эти задачи встречаются во многих отраслях знаний. Алгоритмы их решения хорошо известны. Эти алгоритмы реализованы во многих, как проприетарных, так и свободных, математических пакетах. Не является исключением и Octave. Но перед тем, как рассмотреть решение задач линейного программирования в Octave, давайте вспомним, что такое задача линейного программирования.
10.2.1 Задача линейного программирования
Знакомство с задачами линейного программирования начнём на примере задачи об оптимальном рационе.
Задача об оптимальном рационе. Имеется четыре вида продуктов питания:  . Известна стоимость единицы каждого продукта
. Известна стоимость единицы каждого продукта  . Из этих продуктов необходимо составить пищевой рацион, который должен содержать не более
. Из этих продуктов необходимо составить пищевой рацион, который должен содержать не более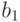 единиц белков, не более
единиц белков, не более  единиц углеводов, не более
единиц углеводов, не более  единиц жиров. Причём известно, в единице продукта П1 содержится
единиц жиров. Причём известно, в единице продукта П1 содержится  единиц белков,
единиц белков,  единиц углеводов и
единиц углеводов и  единиц жиров и т.д. (см. таблицу 10.1).
единиц жиров и т.д. (см. таблицу 10.1).
Требуется составить пищевой рацион, чтобы обеспечить заданные условия при минимальной стоимости.
Пусть  — количества продуктов
— количества продуктов  . Общая стоимость рациона равна
. Общая стоимость рациона равна
 |
( 10.1) |
Сформулируем ограничение на количество белков, углеводов и жиров в виде неравенств. В одной единице продукта  содержится
содержится  единиц белков, в
единиц белков, в 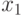 единицах —
единицах —  , в
, в 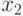 единицах продукта
единицах продукта  содержится
содержится 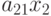 единиц белка и т.д. Следовательно общее количество белков во всех четырёх типов продукта равно
единиц белка и т.д. Следовательно общее количество белков во всех четырёх типов продукта равно  и должно быть не больше
и должно быть не больше 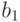 . Получаем первое ограничение
. Получаем первое ограничение
 |
( 10.2) |
Аналогичные ограничения для жиров и углеводов имеют вид:
 |
( 10.3) |
Принимаем во внимание, что  положительные значения, получим ещё четыре ограничения
положительные значения, получим ещё четыре ограничения
 |
( 10.3) |
Таким образом задачу о оптимальном рационе можно сформулировать следующим образом: найти значения переменных  удовлетворяющие системе ограничений (10.2) — (10.4), при которых линейная функция (10.1) принимала бы минимальное значение.
удовлетворяющие системе ограничений (10.2) — (10.4), при которых линейная функция (10.1) принимала бы минимальное значение.
Задача об оптимальном рационе является задачей линейного программирования, функция (10.1) называется функцией цели, а ограничения (10.2) — (10.4) системой ограничений задачи линейного программирования.
В задачах линейного программирования функция цели  и система ограничений являются линейными.
и система ограничений являются линейными.
В общем случае задачу линейного программирования можно сформулировать следующим образом. Найти такие положительные значения  , при которых функция цели
, при которых функция цели  (10.5) достигает своего минимального значения и удовлетворяет системе линейных ограничений (10.6).
(10.5) достигает своего минимального значения и удовлетворяет системе линейных ограничений (10.6).
 |
( 10.5) |
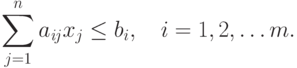 |
( 10.6) |
Если в задачу линейного программирования добавляется ограничение целочисленности значений  , то мы получаем задачу целочисленного программирования.
, то мы получаем задачу целочисленного программирования.
Octave позволяет решать задачи линейной оптимизации с ограничениями в более общей формулировке.
Найти такие положительные значения  , при которых функция цели L (10.5) достигает своего минимального (максимального) значения и удовлетворяет системе линейных ограничений. Система ограничений может быть представлена неравенствами (10.7) или (10.8). При этом значения
, при которых функция цели L (10.5) достигает своего минимального (максимального) значения и удовлетворяет системе линейных ограничений. Система ограничений может быть представлена неравенствами (10.7) или (10.8). При этом значения  могут быть, как вещественными, так и целочисленными, как положительными, так и отрицательными.
могут быть, как вещественными, так и целочисленными, как положительными, так и отрицательными.
 |
( 10.7) |
 |
( 10.8) |
Рассмотрим решение задач линейного программирования в Octave.
