НОУ ИНТУИТ | Введение в Octave. Лекция 9: Решение обыкновенных дифференциальных уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

9.2.2 Решение дифференциальных уравнений при помощи модифицированного метода Эйлера

Более точным методом решения задачи (9.4)–(9.5) является модифицированный метод Эйлера, при котором сначала вычисляют промежуточные значения [2]

$t_p=t_i+\frac{h}{2},\ x_p=x_i+\frac{h}{2}f(x_i,t_i)$

( 9.12)

после чего находят значение $x_{i+1}$ по формуле

$x_{i+1}=x_i+hf(x_p,t_p),\quad i=0,1,\dots, n-1$

( 9.13)

9.2.3 Решение дифференциальных уравнений методами Рунге-Кутта

Рассмотренные выше методы Эйлера (как обычный, так и модифицированный) являются частными случаями явного метода Рунге-Кутта -го порядка. В общем случае формула вычисления очередного приближения методом Рунге-Кутта имеет вид [2]:

$x_{i+1}=x_i+h\varphi (t_i,x_i,h),\quad i=0,1,\dots, n-1$

( 9.14)

Функция $\varphi (t,x,h)$ приближает отрезок ряда Тейлора до -го порядка и не содержит частных производных f (t, x) [2].

Метод Эйлера является методом Рунге-Кутта первого порядка (k = 1) и получается при

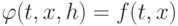
$\varphi (t,x,h) = f (t,x)$

.

Семейство методов Рунге-Кутта второго порядка имеет вид [2]

$x_{i+1}&=x_i+h\Biggl((1-\alpha )f(t_i,x_i)+\alpha f\left(t_i+ \frac{h}{2\alpha },x_i+\frac{h}{2\alpha}f(t_i,x_i)\right)\Biggr),\\ i&=0,1,\dots, n-1$

( 9.15)

Два наиболее известных среди методов Рунге-Кутта второго порядка [2] — это метод Хойна $\alpha=\frac{1}{2}$ и модифицированный метод Эйлера $\alpha=1$ .

Подставив $\alpha=\frac{1}{2}$ в формулу (9.15), получаем расчётную формулу метода Хойна [2]:

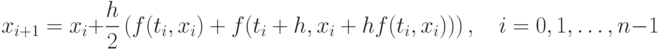
$x_{i+1}=x_i+\frac{h}{2}\left(f(t_i,x_i)+f(t_i+h,x_i+hf(t_i,x_i))\right),\quad i=0,1,\dots, n-1$

Подставив $\alpha=1$ в формулу (9.15), получаем расчётную формулу уже рассмотренного выше модифицированного метода Эйлера

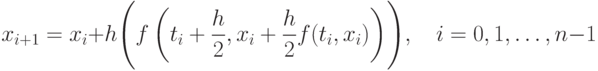
$x_{i+1}=x_i+h\Biggl(f\left(t_i+\frac{h}{2},x_i+\frac{h}{2}f(t_i,x_i)\right)\Biggr),\quad i=0,1,\dots, n-1$

Наиболее известным является метод Рунге-Кутта четвёртого порядка, расчётные формулы которого можно записать в виде [2]:

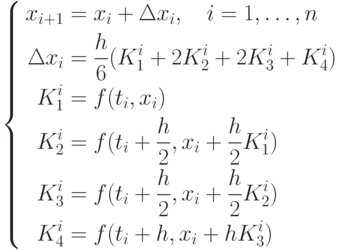
$\left\{ \begin{aligned} x_{i+1} &=x_i+\Delta x_i,\quad i=1,\dots, n\\ \Delta x_i &=\frac{h}{6}(K_1^i+2K_2^i+2K_3^i+K_4^i)\\ K_1^i &=f(t_i,x_i)\\ K_2^i &=f(t_i+\frac{h}{2},x_i+\frac{h}{2}K_1^i)\\ K_3^i &=f(t_i+\frac{h}{2},x_i+\frac{h}{2}K_2^i)\\ K_4^i &=f(t_i+h,x_i+hK_3^i) \end{aligned} \right.$

Одной из модификаций метода Рунге-Кутта является метод Кутта-Мерсона (или пятиэтапный метод Рунге-Кутта четвёртого порядка), который состоит в следующем [2].

i-м шаге рассчитываются коэффициенты
$\begin{aligned} K_{1}^{i}&=f(t_{i},x_{i})\\ K_{2}^{i}&=f(t_{i}+\frac{h}{3},x_{i}+\frac{3}{2}K_{1}^{i})\\ K_{3}^{i}&=f(t_{i}+\frac{h}{3},x_{i}+\frac{h}{6}K_{1}^{i}+\frac{h}{6}K_{2}^{i})\\ K_{4}^{i}&=f(t_{i}+\frac{h}{2},x_{i}+\frac{h}{8}K_{1}^{i}+\frac{3h}{2}K_{2}^{i})\\ K_{5}^{i}&=f(t_{i}+h,x_{i}+\frac{h}{2}K_{1}^{i}-\frac{3h}{2}K_{3}^{i}+2hK_{4}^{i}) \end{aligned}$ ( 9.16)
Вычисляем приближённое значение $x(t_{i+1})$ по формуле
$\tilde {{x}}_{i+1}=x_{i}+\frac{h}{2}(K_{1}^{i}-3K_{3}^{i}+4K_{4}^{i})$ ( 9.17)
Вычисляем приближённое значение $x(t_{i+1})$ по формуле
${x}_{i+1}=x_{i}+\frac{h}{6}(K_{1}^{i}+4K_{3}^{i}+K_{5}^{i})$ ( 9.18)
оценочный коэффициент по формуле
$R=0.2|x_{i+1}-\tilde {x}_{i+1}|$ ( 9.19)
Сравниваем с точностью вычислений $\varepsilon$ . Если
$R\ge \varepsilon$
, то уменьшаем шаг вдвое и возвращаемся к п.1. Если $R< \varepsilon$ , то значение,вычисленное по формуле (9.18), и будет вычисленным значением $x(t_{i+1})$ (с точностью $\varepsilon$ ).
переходом к вычислению следующего значения , сравниваем с $\frac{\varepsilon }{64}$ . Если $R<\frac{\varepsilon }{64}$ , то дальнейшие вычисления можно проводить с удвоенным шагом .

Рассмотренные методы Рунге-Кутта относятся к классу одношаговых методов, в которых для вычисления значения в очередной точке $x_{k+1}$ нужно знать значение в предыдущей точке x_k .

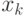Ещё один класс методов решения задачи Коши — многошаговые методы, в которых используются точки $x_{k-3}, x_{k-2}, x_{k-1}, x_{k}$ для вычисления $x_{k+1}$ . В многошаговых методах первые четыре начальные точки $(t_{0},x_{0}),(t_{1},x_{1}),(t_{2},x_{2}),(t_{3},x_{3})$ должны быть получены заранее любым из одношаговых методов (метод Эйлера, Рунге-Кутта и т.д.). Наиболее известными многошаговыми методами являются методы прогноза-коррекции Адамса и Милна.

Дальше >>

Авторизоваться

Введение в Octave

Решение обыкновенных дифференциальных уравнений и систем

9.2.2 Решение дифференциальных уравнений при помощи модифицированного метода Эйлера

9.2.3 Решение дифференциальных уравнений методами Рунге-Кутта

Вопросы и ответы