|
Возможна ли разработка приложения на Octave с GUI? |
Задачи линейной алгебры
5.9 Задачи линейной алгебры в символьных вычислениях
Основы работы с символьными переменными в Octave описаны в п. 2.7. Рассмотрим работу с матрицами, заданными в символьных переменных и выражениях. Для определения символьной матрицы служит функция  (число строк, число столбцов, элементы матрицы).
(число строк, число столбцов, элементы матрицы).
Например:
>>> symbols >>> a = sym( "a" ); % Определение символьных переменных >>> b = sym( "b" ); >>> c = sym( "c" ); >>> d = sym( "d" ); >>> Matr=ex_matrix( 1, 3, a, b, c ) % Матрица строка Matr = [ [ a, b, c ] ] >>> Matr=ex_matrix( 4, 1, a, b, c, d ) % Матрица столбец Matr = [ [ a ], [ b ], [ c ], [ d ] ] >>> Matr=ex_matrix( 2, 2, a, b, c, d ) % Матрица 2 на 2 Matr = [ [ a, b ], [ c, d ] ] >>> Matr=ex_matrix( 3, 3, a, 0, b, c, 1, 1, d, 0, 2 ) % Матрица 3 на 3 Matr = [ [ a, 0.0, b ], [ c, 1.0, 1.0 ], [ d, 0.0, 2.0 ] ]
Над символьными матрицами определены операции сложения, вычитания, умножения.
Пример 5.18. Выполнить действия над матрицами (листинг 5.19).
>>> symbols >>> a = sym ( "a" ); % Определение символьных переменных >>> b = sym ( "b" ); >>> c = sym ( "c" ); >>> d = sym ( "d" ); % Определение матриц >>> A=ex_matrix ( 2, 2, a, b, c, d ) A = [ [ a, b ], [ c, d ] ] >>> B=ex_matrix ( 2, 2, d, b, c, a ) B = [ [ d, b ], [ c, a ] ] >>> C=A+B C = [ [ d+a, 2 * b ], [ 2 * c, d+a ] ] >>> D=A _ B D = [[ -d+a, 0 ], [ 0, d-a ] ] >>> C_D ans = [ [ - ( d -a ) * ( d+a ), 2 * ( d -a ) * b ], [ - 2 * ( d -a ) * c, ( d-a ) * ( d+a ) ] ]Листинг 5.19. Действия над символьными матрицами (пример 5.18).
К сожалению над символьными матрицами не определены операции вычисления определителя и обратной матрицы.
Для решения системы линейных алгебраических уравнений можно воспользоваться функцией  .
.
Пример 5.19. Решить систему линейных алгебраических уравнений  относительно переменных x и y (листинг 5.20).
относительно переменных x и y (листинг 5.20).
>>> x = sym( "x" );
>>> y = sym( "y" );
>>> a = sym( "a" );
>>> b = sym( "b" );
>>> c = sym( "c" );
>>> d = sym( "d" );
>>> sols = symlsolve({ a * x+b * y==c, x+y==d },{ x, y })
sols =
(
[ 1 ] = -(a-b ) ^(-1) * ( d *b-c )
[ 2 ] = -(a-b ) ^( -1) * ( c-d*a )
)
Листинг
5.20.
Решение СЛАУ в символьном виде (пример 5.19).
Пример 5.20. Решить систему линейных алгебраических уравнений (листинг 5.21)
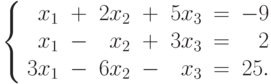
>>> x1 = sym( "x1" );
>>> x2 = sym( "x2" );
>>> x3 = sym( "x3" );
>>> sols = symlsolve({ x1+2*x2+5*x3==-9,x1-x2+3*x3==2,3* x1 -6*x2
-x3==25},{x1, x2, x3 })
sols =
(
[ 1 ] =2.0
[ 2 ] = -3.0
[ 3 ] = -1.0
)
Листинг
5.21.
Решение СЛАУ используя symlsolve (пример 5.20).
