|
Возможна ли разработка приложения на Octave с GUI? |
Построение графиков
4.1.2 Построение графиков в полярной системе координат
Полярная система координат состоит из заданной фиксированной точки  , называемой полюсом, концентрических окружностей с центром в полюсе и лучей, выходящих из точки
, называемой полюсом, концентрических окружностей с центром в полюсе и лучей, выходящих из точки  , один из которых,
, один из которых, 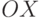 , называют полярной осью. Положение любой точки
, называют полярной осью. Положение любой точки  в полярных координатах можно задать положительным числом ρ = |OM | (полярный радиус) и числом ϕ, равным величине угла ∠XOM (полярный угол). Числа ρ и ϕ называют полярными координатами точки
в полярных координатах можно задать положительным числом ρ = |OM | (полярный радиус) и числом ϕ, равным величине угла ∠XOM (полярный угол). Числа ρ и ϕ называют полярными координатами точки  и обозначают
и обозначают  (ρ, ϕ).
(ρ, ϕ).
Для формирования графика в полярной системе координат необходимо сформировать массивы значений полярного угла и полярного радиуса и обратиться к функции  , где
, где 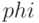 — массив полярных углов; ro — массив полярных радиусов;
— массив полярных углов; ro — массив полярных радиусов;  — строка, состоящая из трёх символов, которые определяют цвет линии, тип маркера и тип линии (см. табл. 4.1, 4.2).
— строка, состоящая из трёх символов, которые определяют цвет линии, тип маркера и тип линии (см. табл. 4.1, 4.2).
В качестве примера использования функции polar рассмотрим решение следующей задачи.
Пример 4.10. Построить график лемнискаты.
Уравнение лемнискаты в полярных координатах имеет вид:  , функция ρ определена при
, функция ρ определена при  . Поэтому листинг для изображения графика лемнискаты будет таким.
. Поэтому листинг для изображения графика лемнискаты будет таким.
fi = -pi/4:pi/200:pi/4; % Определяем массив полярного угла fi. % Определяем массив положительных значений полярного радиуса ro. ro=3*sqrt(2*cos(2*fi)); polar(fi, ro, ’r’); % Рисуем правую часть лемнискаты. hold on; % Блокируем режим очистки окна. polar(fi, -ro, ’r’); % Рисуем левую часть лемнискаты. grid on;Листинг 4.10. Построение графика лемнискаты (пример 4.10).
На рис. 4.10. изображены графики функций: 
Полученный график изображён на рис. 4.11.
Пример 4.11. Построить графики архимедовой спирали, гиперболической спирали и логарифмической спирали в полярных координатах.
Уравнение архимедовой спирали в полярных координатах имеет вид:  , гиперболической —
, гиперболической —  . Соотношение
. Соотношение  является уравнением логарифмической спирали в полярных координатах. Частным случаем логарифмической спирали (
является уравнением логарифмической спирали в полярных координатах. Частным случаем логарифмической спирали (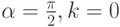 ) является уравнение окружности (
) является уравнение окружности ( ).
).
В листинге 4.11 приведён текст программы, позволяющей построить в одном графическом окне четыре оси координат, в каждом из которых построить свой график — архимедову, гиперболическую и логарифмическую спирали, а также окружность.
График представлен на рис. 4.12.
h=figure( ) clear all; % Формируем массивы fi1, fi2, fi3, fi4, ro1, ro2, ro3, ro4. fi1 =0:pi/20:6*pi; fi 2=pi/3:pi /200:6*pi; fi3 =0:pi/20:4*pi; fi4 = -pi:pi/20:pi; ro1=4* f i 1; ro2 =0.5./fi2; ro3=4*exp(0.2*fi3); for i = 1:41 ro4(i) =4; endfor % Делим графическое окно на 4 части и объявляем первый график текущим. subplot(2, 2, 1); polar(fi1, ro1); % Строим график архимедовой спирали. title(’Graph of Archimedean spiral’); % Подписываем график. subplot(2, 2, 2); % Второй график объявляем текущим. polar(fi2, ro2); % Строим график гиперболической спирали. title(’Graph of the hyperbolic spiral’); % Подписываем график. subplot(2, 2, 3); % Третий график объявляем текущим. polar(fi3, ro3); % Строим график логарифмической спирали. title(’Graph of the logarithmic spiral’); % Подписываем график. subplot(2, 2, 4); % Четвёртый график объявляем текущим. polar(fi4, ro4); % Строим график окружности. title(’Graph the circle’); % Подписываем график.Листинг 4.11. Построение графиков спиралей (пример 4.11).


