Основы работы

2.7 Символьные вычисления

Символьные вычисления в Octave поддерживает специальный пакет расширений octave-symbolic. Процедура установки пакетов расширений описана в первой главе. Если пакет уже установлен, то перед началом работы его нужно загрузить командой pkg load symbolic. Теперь можно использовать любые функции из пакета symbolic.

Оператор symbols инициализирует символические операции, с этого оператора должны начинаться любые действия в символьных переменных. Работа с символьными переменными в Octave требует их специального объявления: sym(’имя переменной’). Например, команда x = sym ("x") объявляет символьную переменную .

Пример 2.2. Выполнить арифметические операции с символьными переменными , где (листинг 2.2).

	
>>> x = sym ( "x" );% Объявление
>>> y = sym ( "y" );% символьных
>>> z = sym ( "z" );% переменных
>>> t = sym ( "t" );
>>> a = sym ( "a" );
>>> b = sym ( "b" );
% Вычисление символьных выражений
>>> x=a+b
x = a+b
>>> y=a^2-b^2
y = -b ^ (2.0)+a ^ ( 2.0 )
>>> z=x*y
z = -(b ^ ( 2.0 )-a ^ ( 2.0 ) ) *( a+b )
>>> t=x^3/ z
t = -(b ^ ( 2.0 )-a ^ ( 2.0 ) ) ^( -1) *( a+b ) ^ ( 2.0 )

Символьные вычисления в Octave предусматривают работу с элементарными математическими функциями (таблица 2.11).

Таблица 2.11. Функции в символьных вычислениях

Функция	Описание функции
	синус числа
	косинус числа
	тангенс числа
	арксинус числа
	арккосинус числа
	арктангенс числа
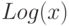	натуральный логарифм числа
	экспонента числа
	корень квадратный из числа
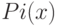	число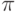

Вычислить значение символьного выражения при заданном значении переменной можно с помощью функции

subs(выражение,имя переменной,значение переменной)

Пример 2.3. Вычислить значение выражения: , при (листинг 2.3).

	
>>> x = sym ( "x" );
>>> y = sym ( "y" );
>>> y=Sin ( x )^2-Cos ( x ) ^2
y = -cos ( x ) ^ ( 2.0 )+sin ( x ) ^ ( 2.0 )
% Значение выражения при заданном значении переменной
>>> subs ( y, x, Pi /3)
ans = 0.5000000000000000001
>>> subs ( y, x, Pi /6)
ans = -0.4999999999999999999

Преобразовать символьное выражение, представить его в виде элементарных функций возможно командой

expand(выражение)

Пример 2.4. Раскрыть скобки в выражении (листинг 2.1).

	
>>> y=( Sqrt ( x ) +1) *( Sqrt ( x ) -1)+(x-1) *( x -1) *( x -1)
y = ( -1.0+x ) ^3+(-1.0+ sqrt ( x ) ) *(1.0+ sqrt ( x ) )
>>> expand ( y )
ans = -2.0+(4.0) *x+x ^3 -(3.0) *x^2

Далее, по ходу изложения материала, будут рассмотрены операции с матрицами символов, решение систем линейных уравнений в символьных переменных (п. 5.9), решение нелинейных уравнений и систем (п. 7.4), дифференцирование (п. 8.1).