Ортогональные линейные трансформации
Квантовый алгоритм является линейной трансформацией в пространстве кубитов, но эта трансформация специального вида - ортогональная линейная трансформация.
Определение. Линейная трансформация Т в векторном пространстве  называется ортогональной, если образы базисных векторов
называется ортогональной, если образы базисных векторов  ортогональны друг другу и все они имеют единичную длину
ортогональны друг другу и все они имеют единичную длину
Определение. Множество из N взаимно ортогональных векторов длины 1 в  называется ортонормальным базисом
называется ортонормальным базисом  .
.
Матрица ортогональной трансформации называется ортогональной матрицей.
Главные свойства ортогональных матриц: скалярное произведение любых двух столбцов ортогональной матрицы равно нулю; скалярное произведение любого столбца с самим собой равно единице. Эти свойства непосредственно следуют из определения ортогональных матриц.
Давайте рассмотрим несколько примеров ортогональных трансформаций:
-
Поворот в
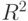 на угол
на угол  . Из геометрии ясно, что вектора
. Из геометрии ясно, что вектора 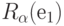 и
и  являются единичными векторами и ортогональны друг другу Нетрудно проверить, что и скалярные произведения столбцов матрицы
являются единичными векторами и ортогональны друг другу Нетрудно проверить, что и скалярные произведения столбцов матрицы  ( удовлетворяют всем указанным свойствам:
( удовлетворяют всем указанным свойствам:
- Отражение в
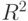 относительно линии, проходящей через начало координат. Эта трансформация является ортогональной, поскольку зеркальное отражение сохраняет длину вектора и углы между векторами.
относительно линии, проходящей через начало координат. Эта трансформация является ортогональной, поскольку зеркальное отражение сохраняет длину вектора и углы между векторами. - Поворот в
 на угол
на угол  а вокруг некоторой оси, проходящей через начало координат.
а вокруг некоторой оси, проходящей через начало координат.
Фактически можно показать, что любая ортогональная трансформация в 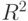 представляет собой либо поворот, либо отражение, как в выше приведенных примерах 1-2. Приведем некоторые аргументы в пользу этого утверждения. Пусть Т - ортогональная трансформация в
представляет собой либо поворот, либо отражение, как в выше приведенных примерах 1-2. Приведем некоторые аргументы в пользу этого утверждения. Пусть Т - ортогональная трансформация в 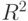 и пусть
и пусть  . Так как Т - ортогональна, то
. Так как Т - ортогональна, то  и
и  - единичные вектора, ортогональные друг другу Все единичные вектора на плоскости могут быть получены друг из друга в результате поворота на некоторый угол. Предположим, что
- единичные вектора, ортогональные друг другу Все единичные вектора на плоскости могут быть получены друг из друга в результате поворота на некоторый угол. Предположим, что  получено поворотом
получено поворотом  на угол
на угол  против часовой стрелки.
против часовой стрелки.
Тогда:

Так как вектор  перпендикулярен
перпендикулярен  , то существуют лишь две возможности получения
, то существуют лишь две возможности получения  из
из  путем поворота - повернуть
путем поворота - повернуть  на
на 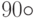 против часовой стрелки, либо по часовой стрелке:
против часовой стрелки, либо по часовой стрелке:
В первом случае Т - это поворот с матрицей, записанной выше, во-втором случае - поворот с матрицей:

Далее мы собираемся установить несколько свойств ортогональных трансформаций.
Теорема. Линейная трансформация Т ортогональна, если и только если она сохраняет скалярное произведение:
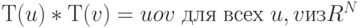
Доказательство. Предположим, что Т ортогонально. Из определения ортогональной трансформации следует, что утверждение справедливо для базисных векторов:  . Для доказательства истинности утверждения для произвольных векторов u и v представим их в виде линейной комбинации базисных векторов:
. Для доказательства истинности утверждения для произвольных векторов u и v представим их в виде линейной комбинации базисных векторов:

Тогда
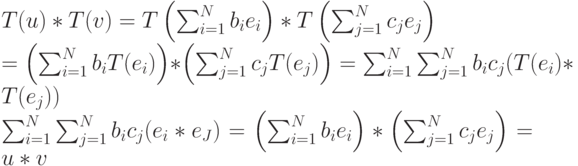
Мы заключаем, что Т сохраняет скалярное произведение.
Доказательство в другую сторону следует из того, что если Т сохраняет скалярное произведение, то  . Так что Т преобразует базис
. Так что Т преобразует базис  в другой ортонормальный базис. Следовательно, Т - ортогональная трансформация.
в другой ортонормальный базис. Следовательно, Т - ортогональная трансформация.
Из теоремы следует, что ортогональная трансформация сохраняет длину вектора и углы между векторами, поскольку эти характеристики можно выразить через скалярное произведение.
Заметим также, что скалярное произведение двух векторов может быть выражено, используя длины векторов:

Следовательно, любая линейная трансформация, сохраняющая длины векторов, также сохраняет их скалярное произведение и должна быть ортогональной. Итогом приведенного обсуждения является следующая
Теорема. Следующие четыре утверждения эквивалентны:

