Реализация некоторых численных методов

8.1.2 Метод простых итераций

В ряде случаев весьма удобным приёмом уточнения корня уравнения является метод последовательных приближений (метод итераций).

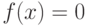Пусть с точностью необходимо найти корень уравнения , принадлежащий интервалу изоляции . Функция и ее первая производная непрерывны на этом отрезке.

Для применения этого метода исходное уравнение 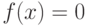должно быть приведено к виду .

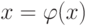В качестве начального приближения может быть выбрана любая точка интервала .

Далее итерационный процесс поиска корня строится по схеме:

В результате итерационный процесс поиска реализуется рекуррентной формулой. Процесс поиска прекращается, как только выполняется условие или число итераций превысит заданное число .

Для того, чтобы последовательность приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости .

Пример реализации метода итераций представлен ниже:

(%i1)	f:exp(-x)-x$
beta:0.1$ x1:1$ x0:0$ eps:0.000001$ p:0$
while abs(x1-x0)>eps do
		(x0:x1, p:p+1, x1:float(x0+beta*(subst(x0,x,f))))$
print("Число итераций ",p," ","Решение ",float(x1),
" Невязка ",float(abs(x1-x0)))$

8.1.3 Метод Ньютона (метод касательных)

Рассмотренные ранее методы решения нелинейных уравнений являются методами прямого поиска. В них для нахождения корня используется нахождение значения функции в различных точках интервала .

Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.

Рассмотрим нелинейное уравнение 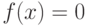, для которого необходимо найти корень на интервале с точностью .

Метод Ньютона основан на замене исходной функции , на каждом шаге поиска касательной, проведённой к этой функции. Пересечение касательной с осью дает приближение корня.

Выберем начальную точку (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью дает первое приближение корня :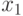

Поэтому .

В результате, итерационный процесс схождения к корню реализуется рекуррентной формулой

Процесс поиска продолжаем до тех пор, пока не выполнится условие: 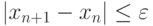, откуда .

Метод обеспечивает быструю сходимость, если выполняется условие: , т.е. первую касательную рекомендуется проводить в той точке интервала , где знаки функции и ее кривизны 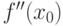совпадают.

Пример реализации метода Ньютона в Maxima представлен ниже:

(%i1)	newton(f,x0,eps):=block([df,xn,xn0,r,p],
	xn0:x0, df:diff(f,x),
	p:0, r:1,
	while abs(r)>eps do (
		p:p+1, xn:xn0-float(subst(xn0,x,f)/subst(xn0,x,df)),
		print("x0,x1 ",xn0,xn),r:xn-xn0, xn0:xn
	),
	[xn,p])$

Последовательность команд для обращения к функции и результаты вычислений представлены в следующем примере:

(%i2)	f:exp(-x)-x$
	eps:0.000001$ xrez:newton(f,1,eps)$
	print("Решение ",xrez[1]," Число итераций ",xrez[2],
	" Невязка ",subst(xrez[1],x,f))$

Особенности приведённого примера — промежуточная печать результатов и возвращаемое значение в виде списка, что позволяет одновременно получить как значение корня, так и необходимое для достижения заданной точности число итераций. Существенному уменьшению числа итераций способствует и аналитическое вычисление производной.