Академия ALT Linux:

Компьютерная математика с Maxima
[+]
Компания ALT Linux
Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 553 / 138 | Длительность: 19:00:00
Темы: Математика, Программное обеспечение, Физика
Специальности: Математик, Преподаватель, Физик
Лекция 7:

Решение физических и математических задач с Maxima
A
|
версия для печати
< Лекция 6 || Лекция 7: 123 || Лекция 8 >

7.2 Некоторые физические задачи

Применение систем символьной математики в преподавании физики и химии позволяет сосредоточиться на содержательной части преподаваемого материала. Кроме того, учащиеся получают возможность решать куда более сложные задачи, чем при ручных расчётах. Наличие в Maxima чётко выраженного алгоритмического языка (в отличие от Matcad) существенно снижает риск подмены понятий, когда пробелы собственного подхода к решению задачи учащиеся относят на наличие ошибок и неточностей в программном обеспечении.

Идеи рассмотренных задач взяты из известных руководств по использованию MathCad, однако, по мнению автора, использование Maxima может быть не менее, а во многих случаях и более эффективным.

7.2.1 Вычисление средней квадратичной скорости молекул

Выражение, содержащие переменные, по существу может использоваться в качестве функции пользователя в Maxima.

Рассмотрим возможность вычисления среднеквадратичной скорости молекул для различных газов. Используемая формула: v = \sqrt{\frac{3RT}{M}} , где R = 8.314 Дж/(моль \cdot К), T — абсолютная температура, M — молярная масса.

Вычислим среднеквадратичную скорость молекул CO_2 (M = 0.044 кг/моль) при температуре 273 К:

(%i1)	v:sqrt(3*R*T/M);
(\%o1)\quad \sqrt{3}\,\sqrt{\frac{R\,T}{M}}
(%i2)	vCO2:float(v),M=0.044,T=273,R=8.314;
(\%o2)\quad 393.3875604633079

Расчёт для нескольких различных газов несложно провести, варьируя молярную массу:

(%i3)	vVozd:float(v),M=0.029,T=273,R=8.314;
(\%o3)\quad 484.5604478145187
(%i4)	vH2:float(v),M=0.002,T=273,R=8.314;
(\%o4)\quad 1845.151213315592

7.2.2 Распределение Максвелла

Аналогично предыдущему расчёту создадим выражение, описывающее распределение Максвелла (см. блок команд Maxima ниже).

(%i1)	fun:4*%pi*(M/2/%pi/R/T)^(3/2)*exp(-M*v^2/2/R/T)*v^2;
(\%o1)\quad \frac{2\,{v}^{2}\,{\left( \frac{M}{R\,T}\right) }^{\frac{3}{2}}\,{e}^{-\frac{{v}^{2}\,M}{2\,R\,T}}}{\sqrt{2}\,\sqrt{\pi }}

Для анализа полученных выражений в формулу распределения Максвелла подставляем только температуру:

(%i2)	fun70:fun,T=70;
(\%o2)\quad \frac{{v}^{2}\,{\left( \frac{M}{R}\right) }^{\frac{3}{2}}\,{e}^{-\frac{{v}^{2}\,M}{140\,R}}}{35\,\sqrt{2}\,\sqrt{70}\,\sqrt{\pi }}
(%i3)	fun150:fun,T=150;
(\%o3)\quad \frac{{v}^{2}\,{\left( \frac{M}{R}\right) }^{\frac{3}{2}}\,{e}^{-\frac{{v}^{2}\,M}{300\,R}}}{375\,\sqrt{2}\,\sqrt{6}\,\sqrt{\pi }}
(%i4)	fun300:fun,T=300;
(\%o4)\quad \frac{{v}^{2}\,{\left( \frac{M}{R}\right) }^{\frac{3}{2}}\,{e}^{-\frac{{v}^{2}\,M}{600\,R}}}{1500\,\sqrt{2}\,\sqrt{3}\,\sqrt{\pi }}
Распределение Максвелла по скоростям молекул воздуха для различных температур

увеличить изображение
Рис. 7.1. Распределение Максвелла по скоростям молекул воздуха для различных температур

Для построения графика зависимости функции распределения от температуры подставляем молярную массу воздуха и величину универсальной газовой постоянной (см. результаты на рис. 7.1):

(%i5)	plot2d([fun70,fun150,fun300],[v,0,1000]),M=0.029,R=8.314;

Можно изучить влияние температуры на форму кривой, а так- же на положение максимума функции распределения. С помощью интегрирования f(v) можно посчитать долю молекул, обладающих скоростями в каком-либо интервале, а также определить среднюю и среднюю квадратичную скорости молекул.

Пример:

(%i6)	integrate(v*v*fun,v,0,inf);
Is M\,R\,T positive, negative, or zero?
p;
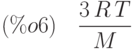
(\%o6)\quad \frac{3\,R\,T}{M}

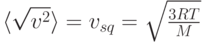Таким образом, \langle v^2 \rangle = \frac{3RT}{M} , откуда среднеквадратичная скорость молекул газа \langle \sqrt{v^2} \rangle = v_{sq}= \sqrt{\frac{3RT}{M}} .

7.2.3 Броуновское движение

Наличие генератора случайных чисел дает возможность моделировать движение броуновской частицы.

Траектория броуновского движения модельной частицы

увеличить изображение
Рис. 7.2. Траектория броуновского движения модельной частицы

Эйнштейн первый рассчитал параметры броуновского движения, показав, что нерегулярное перемещение частиц, взвешенных в жидкости, вызвано случайными ударами соседних молекул, совершающих тепловое движение. 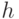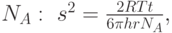В соответствии с теорией Смолуховского- Эйнштейна, среднее значение квадрата смещения броуновской частицы (s^2) за время t прямо пропорционально температуре T и обратно пропорционально вязкости жидкости h, размеру частицы r и постоянной Авогадро N_A:\ s^2 = \frac {2 R T t}{6 \pi h r N_A },, где R — газовая постоянная.

Броуновские частицы имеют размер порядка 0,1–1 мкм, т.е. от одной тысячной до одной десятитысячной доли миллиметра.

Построим несколько упрощённую модель броуновского движения, предполагая, что смещение частицы по каждой из координат — нормально распределённая случайная величина с нулевым математическим ожиданием. Для генерации случайных чисел используем пакет distrib, включающий необходимые функции (использован генератор random_normal).

(%i1)	load("distrib")$
	x:0$ y:0$ xy:[[0,0]]$ m:0$ s:1$
	Nmax:500$ for i:1 thru Nmax do (x:x+random_normal(m,s),
	y:y+random_normal(m,s), xy:append(xy,[[x,y]]))$
	plot2d([discrete,xy]);

Результат построения графика приведен на рис. 7.2.

Дальше >>
< Лекция 6 || Лекция 7: 123 || Лекция 8 >

Вопросы и ответы

вопросов: 0