Численные методы и программирование с Maxima

4.3 Встроенные численные методы

4.3.1 Численные методы решения уравнений

4.3.1.1 Решение уравнений с одним неизвестным

Для решения уравнения с одним неизвестным в пакете Maxima предусмотрена функция . Синтаксис вызова:

Поиск корня функции или выражения expr относительно переменной x осуществляется в пределах .

Для поиска корней используется метод деления пополам или, если исследуемая функция достаточно гладкая, метод линейной интерполяции.

4.3.2 Решение уравнений методом Ньютона: пакет newton1

Основная функция пакета newton1 предназначена для решения уравнений методом Ньютона.

Синтаксис вызова:

Данная функция возвращает приближенное решение уравнения 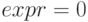методом Ньютона, рассматривая как функцию одной переменной . Поиск начинается с и производится, пока не будет достигнуто условие . Функция допускает наличие неопределенных переменных в выражении , при этом выполнение условия , оценивается как истинное или ложное. Таким образом, нет необходимости оценивать только как число.

Для использования пакета необходимо загрузить его командой load(newton1).

Примеры использования функции :

(%i1)	load (newton1);

(%i2)	newton (cos (u), u, 1, 1/100);

(%i3)	ev (cos (u), u = %);

(%i4)	assume (a > 0);

(%i5)	newton (x^2 - a^2, x, a/2, a^2/100);

(%i6)	ev (x^2 - a^2, x = %);

4.3.2.1 Решение уравнений с несколькими неизвестными: пакет mnewton

Мощная функция для решения систем нелинейных уравнений методом Ньютона входит в состав пакета mnewton. Перед использованием пакет необходимо загрузить:

(%i1)	load("mnewton");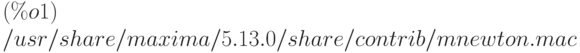

После загрузки пакета mnewton становятся доступными основная функция — и ряд дополнительных переменных для управления ею: (точность поиска, величина по умолчанию 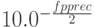), (максимальное число итераций, величина по умолчанию 50).

Синтаксис вызова: , где — список функций, образующих решаемую систему уравнений, 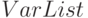— список имен переменной, и — список начальных приближений.

Решение возвращается в том же самом формате, который использует функция . Если решение не найдено, возвращается пустой список.

Пример использования функции :

(%i1)	load("mnewton")$
(%i2)	mnewton([x1+3*log(x1)-x2^2,2*x1^2-x1*x2-5*x1+1],
		[x1, x2], [5, 5]);

(%i3)	mnewton([2*a^a-5],[a],[1]);

Как видно из второго примера, функция может использоваться и для решения единичных уравнений.

4.3.3 Интерполяция

Для выполнения интерполяции функций, заданных таблично, в составе Maxima предусмотрен пакет расширения interpol, позволяющий выполнять линейную или полиномиальную интерполяцию Пакет включает служебную функцию , которая возвращает , если число принадлежит интервалу , и в противном случае.

4.3.3.1 Линейная интерполяция

Линейная интерполяция выполняется функцией Синтаксис вызова: или .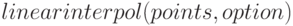

Аргумент должен быть представлен в одной из следующих форм:

• матрица с двумя столбцами, например p:matrix([2,4], [5,6], [9,3]), при этом первое значение пары или первый столбец матрицы — это значения независимой переменной,
• список пар значений, например p:[[2,4], [5,6], [9,3]],
• список чисел, которые рассматриваются как ординаты интерполируемой функции, например p:[4,6,3], в этом случае абсциссы назначаются автоматически (принимают значения 1, 2, 3 и т.д.).

В качестве опции указывается имя независимой переменной, относительно которой строится интерполяционная функция.

Примеры выполнения линейной интерполяции:

(%i1)	load("interpol")$
(%i2)	p: matrix([7,2],[8,2],[1,5],[3,2],[6,7])$
(%i3)	linearinterpol(p);

(%i4)	f(x):="%;

(%i5)	map(f,[7.3,25/7,%pi]);

4.3.3.2 Интерполяция полиномами Лагранжа

Интерполяция полиномами Лагранжа выполняется при помощи функции .

Синтаксис вызова: или .

Смысл параметров и аналогичен указанному выше.

Пример использования интерполяции полиномами Лагранжа:

(%i1)	load("interpol")$
(%i2)	p:[[7,2],[8,2],[1,5],[3,2],[6,7]]$
(%i3)	lagrange(p);

(%i4)	f(x):="%;

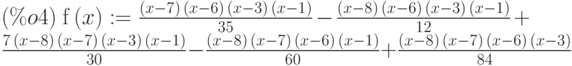
(%i5)	map(f,[2.3,5/7,%pi]);

(%i6)	%,numer;

4.3.3.3 Интерполяция сплайнами

Интерполяция кубическими сплайнами выполняется при помощи функции .

Синтаксис вызова: 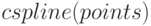или .

Смысл параметров и аналогичен указанному выше.

Пример использования интерполяции кубическими сплайнами:

(%i1)	load("interpol")$
(%i2)	p:[[7,2],[8,2],[1,5],[3,2],[6,7]]$
(%i3)	cspline(p);

(%i4)	f(x):="%;

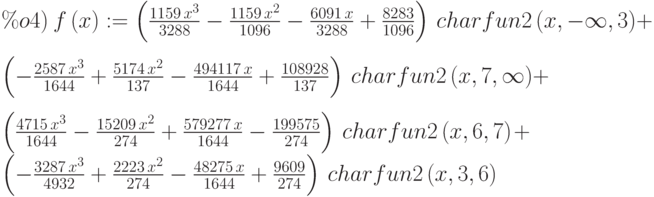
(%i5)	map(f,[2.3,5/7,%pi]);

(%i6)	%,numer;