Задачи высшей математики с Maxima
3.8 Решение дифференциальных уравнений в Maxima
3.8.1 Основные определения
Дифференциальным уравнением называется уравнение вида  , где
, где 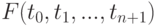 — функция, определенная в некоторой области
— функция, определенная в некоторой области 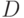 пространства
пространства  — независимая переменная,
— независимая переменная,  — функция от
— функция от  — ее производные.
— ее производные.
Порядком уравнения n называется наивысший из порядков производных  , входящих в уравнение. Функция
, входящих в уравнение. Функция 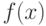 называется решением дифференциального уравнения на промежутке
называется решением дифференциального уравнения на промежутке 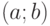 , если для всех
, если для всех 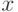 из
из 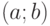 выполняется равенство:
выполняется равенство:  .
.
Дифференциальному уравнению удовлетворяет бесконечное множество функций, но при некоторых условиях решение такого уравнения единственное. Интегральная кривая — это график решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.
Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Пример: решить уравнение  .
.
Очевидно, что его решение  определено на
определено на  . Отметим, что эта постоянная –– произвольная и решение — не единственное, а имеется бесконечное множество решений.
. Отметим, что эта постоянная –– произвольная и решение — не единственное, а имеется бесконечное множество решений.
Пример: Решить уравнение  , или
, или  .
.
Преобразуя уравнение, получим:  . Интегрируя обе части уравнения, получим:
. Интегрируя обе части уравнения, получим:  , или
, или  . Общее решение изображается серией линейных интегральных кривых, проходящих через точку (0,0). При этом через любую точку, не принадлежащую (0, 0), проходит только одна интегральная кривая (решение).
. Общее решение изображается серией линейных интегральных кривых, проходящих через точку (0,0). При этом через любую точку, не принадлежащую (0, 0), проходит только одна интегральная кривая (решение).
Общее решение — множество решений дифференциального уравнения  есть совокупность функций
есть совокупность функций  . Частное решение получают при подстановке конкретного значения константы в общее решение. Особые решения не входят в общие решения, и через каждую точку особого решения проходит более одной интегральной кривой. Особые решения нельзя получить из общего решения ни при каких значениях постоянной
. Частное решение получают при подстановке конкретного значения константы в общее решение. Особые решения не входят в общие решения, и через каждую точку особого решения проходит более одной интегральной кривой. Особые решения нельзя получить из общего решения ни при каких значениях постоянной  . Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Пример: Рассмотрим уравнение  . Преобразуя его, найдём:
. Преобразуя его, найдём:
 . Интегрируя, получаем
. Интегрируя, получаем
 .
.
Пример: Дифференциальное уравнение  имеет общее решение
имеет общее решение  и особое решение
и особое решение  . При конкретном значении
. При конкретном значении
 (например,
(например,  ) получаем частное решение:
) получаем частное решение: 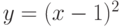 .
.
Геометрически множество решений дифференциального уравнения представляется в виде поля направлений. В каждой точке области, в которой определено поле направлений, задаётся прямая с угловым коэффициентом, равным производной решения. Касательная ко всем подобным прямым и даёт интегральную кривую.
Возможность однозначного решения дифференциального уравнения определяется теоремой единственности:
Пусть  — непрерывная функция в области
— непрерывная функция в области  , причём частная производная
, причём частная производная 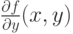 также непрерывна в
также непрерывна в 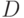 . Тогда существует единственное решение
. Тогда существует единственное решение  дифференциального уравнения
дифференциального уравнения  с начальным условием
с начальным условием  . Следовательно, через точку
. Следовательно, через точку 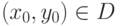 проходит только одна интегральная кривая.
проходит только одна интегральная кривая.
3.8.2 Функции для решения дифференциальных уравнений в Maxima
В Maxima предусмотрены специальные средства решения задачи Коши для систем обыкновенных дифференциальных уравнений, заданных как в явной форме  , так и в неявной
, так и в неявной 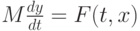 , где
, где  — матрица, — т.н. решатель ОДУ (
— матрица, — т.н. решатель ОДУ (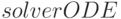 ), обеспечивающий пользователю возможность выбора метода, задания начальных условий и др.
), обеспечивающий пользователю возможность выбора метода, задания начальных условий и др.
Функция  позволяет решить обыкновенные дифференциальные уравнения первого и второго порядков.
позволяет решить обыкновенные дифференциальные уравнения первого и второго порядков.
Синтаксис вызова 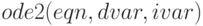 , где
, где  — выражение, определяющее само дифференциальное уравнение, зависимая переменная —
— выражение, определяющее само дифференциальное уравнение, зависимая переменная —  , независимая переменная —
, независимая переменная —  .
.
Дифференциальное уравнение представляется в форме с "замороженной" производной (т.е. с производной, вычисление которой запрещено с помощью одиночной кавычки: 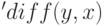 ). Другой вариант явно указать зависимость
). Другой вариант явно указать зависимость  — использовать функцию
— использовать функцию  (в этом случае можно не использовать начальный апостроф см. при-
мер). Если ode2 не может получить решение, она возвращает значение
(в этом случае можно не использовать начальный апостроф см. при-
мер). Если ode2 не может получить решение, она возвращает значение  .
.
Посредством функции  могут быть решены следующие типы ОДУ первого порядка: линейные, ОДУ с разделяющимися переменными, однородные ОДУ, уравнения в полных дифференциалах, уравнения Бернулли, обобщённые однородные уравнения.
могут быть решены следующие типы ОДУ первого порядка: линейные, ОДУ с разделяющимися переменными, однородные ОДУ, уравнения в полных дифференциалах, уравнения Бернулли, обобщённые однородные уравнения.
Кроме того, при помощи функции  могут быть решены следующие типы уравнений второго порядка: с постоянными коэффициентами; в полных дифференциалах; линейные однородные с переменными коэффициентами, которые могут быть сведены к уравнениям с постоянными коэффициентами; уравнения Эйлера; уравнения, разрешимые методом вариации постоянных; уравнения, свободные от независимой переменной, допускающие понижение порядка.
могут быть решены следующие типы уравнений второго порядка: с постоянными коэффициентами; в полных дифференциалах; линейные однородные с переменными коэффициентами, которые могут быть сведены к уравнениям с постоянными коэффициентами; уравнения Эйлера; уравнения, разрешимые методом вариации постоянных; уравнения, свободные от независимой переменной, допускающие понижение порядка.
Тип используемого метода сохраняется в переменной  . При использовании интегрирующего множителя он сохраняется в переменной
. При использовании интегрирующего множителя он сохраняется в переменной 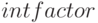 . Частное решение неоднородного уравнения сохраняется в переменной
. Частное решение неоднородного уравнения сохраняется в переменной  .
.
Для отыскания частных решений задач Коши с начальными условиями используются функции  (для уравнений первого порядка) и
(для уравнений первого порядка) и  (для уравнений второго порядка). Частные решения граничных задач для уравнений второго порядка используют функцию
(для уравнений второго порядка). Частные решения граничных задач для уравнений второго порядка используют функцию  .
.
Рассмотрим примеры использования функции  .
.
Вариант использования отложенного дифференцирования (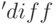 ):
):
(%i1) ode2('diff(y,x)=2*y+exp(x),y,x);
Вариант с явным указанием зависимости  :
:
(%i1) depends(y,x);
![[y\left( x\right) ]\leqno{(\%o1) }](/sites/default/files/tex_cache/d0fb0e3cd5c121d1c846c60cd374ce4f.png)
(%i2) ode2(diff(y,x)=2*y+exp(x),y,x);

Параметр  — постоянная интегрирования для уравнения первого порядка.
— постоянная интегрирования для уравнения первого порядка.
Решение уравнения второго порядка:
(%i4) ode2('diff(y,x,2)-3*'diff(y,x)+2*y=0,y,x);
Параметры  и
и  — постоянные интегрирования для уравнений второго порядка.
— постоянные интегрирования для уравнений второго порядка.
Рассмотрим варианты вычисления частных решений: для уравнения первого порядка
(%i5) ic1(%o1,x=1,y=1);

для уравнения второго порядка
(%i6) ic2(%o4,x=0,y=1,diff(y,x)=1);

3.8.3 Решение основных типов дифференциальных уравнений
3.8.3.1 Уравнения с разделяющимися переменными
Уравнениями с разделяющимися переменными называются уравнения вида  , где
, где 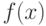 — функция, непрерывна на некотором интервале (
— функция, непрерывна на некотором интервале ( ), а функция
), а функция 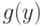 — функция, непрерывна на интервале (
— функция, непрерывна на интервале ( ), причем
), причем  на (
на ( )).
)).
Преобразуя уравнение, получаем: 
Интегрируя обе части, получаем  . Обозначая
. Обозначая  любую первообразную для
любую первообразную для  , а
, а  — любую первообразную для
— любую первообразную для 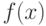 , получаем общее решение дифференциального уравнения в виде неявно выраженной функции
, получаем общее решение дифференциального уравнения в виде неявно выраженной функции  .
.
Пример решения в Maxima:
Отыскиваем общее решение:
(%i1) difur1:'diff(y,x)=sqrt(1-y^2)/sqrt(1-x^2);

(%i2) rez:ode2(difur1,y,x);

Отыскиваем различные варианты частных решений:
(%i3) ic1(rez,x=0,y=0);

(%i4) ic1(rez,x=0,y=1);

3.8.3.2 Однородные уравнения
Под однородными уравнениями понимаются уравнения вида  . Для их решения используется замена вида
. Для их решения используется замена вида  , после подстановки которой получается уравнение с разделяющимися переменными:
, после подстановки которой получается уравнение с разделяющимися переменными:  . Разделяя переменные и интегрируя, получаем:
. Разделяя переменные и интегрируя, получаем: 
Пример решения в Maxima:
Находим общее решение:
(%i1) homode:'diff(y,x) = (y/x)^2 + 2*(y/x);

(%i2) ode2(homode,y,x);

Находим частное решение:
(%i3) ic1(%,x=2,y=1);

Более общий вариант дифференциальных уравнений, уравнения вида:  — сводим их к однородным. Maxima не способна решать такие уравнения при помощи
— сводим их к однородным. Maxima не способна решать такие уравнения при помощи  непосредственно, а лишь после необходимого преобразования.
непосредственно, а лишь после необходимого преобразования.
3.8.3.3 Линейные уравнения первого порядка
Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

 равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть
равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть  не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. При этом
не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. При этом 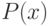 и
и  — функции непрерывные на некотором промежутке
— функции непрерывные на некотором промежутке  .
.Рассмотрим решение линейного дифференциального уравнения в Maxima:
(%i1) lineq1:'diff(y,x)-y/x=x;

(%i2) ode2(lineq1,y,x);

При работе с Maxima не требуется приводить дифференциальное уравнение к стандартной форме вида

(%i3) lineq2:y^2-(2*x*y+3)*'diff(y,x)=0;

(%i4) ode2(lineq2,y,x);

3.8.3.4 Уравнения в полных дифференциалах
Дифференциальное уравнение первого порядка вида:
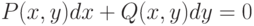
 . Данное дифференциальное уравнение является уравнением в полных дифференциалах, если выполняется условие:
. Данное дифференциальное уравнение является уравнением в полных дифференциалах, если выполняется условие:
Общий интеграл уравнения имеет вид 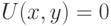 .
.
Если уравнение 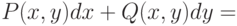 0 не является уравнением в полных дифференциалах, но выполняются условия теоремы единственности, то существует функция
0 не является уравнением в полных дифференциалах, но выполняются условия теоремы единственности, то существует функция  (интегрирующий множитель) такая, что
(интегрирующий множитель) такая, что

Функция 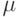 удовлетворяет условию:
удовлетворяет условию:
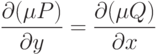
Примеры решения в Maxima:
Для решения в Maxima дифференциальное уравнение представляется в форме

Уравнение, приводимое к уравнению в полных дифференциалах
(%i1) deq:(2*x*y+x^2*y+y^3/3)+(x^2+y^2)*'diff(y,x)=0;

(%i2) ode2(deq,y,x);

Указание на интегрирующий множитель
(%i3) intfactor;

Указание на использованный метод
(%i4) method;

Уравнение в полных дифференциалах
(%i5) deq1:(3*x^2+6*x*y^2)+(6*x^2*y+4*y^3)*'diff(y,x)=0;
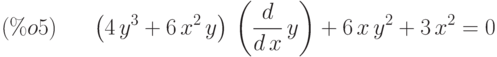
(%i6) ode2(deq1,y,x);

Указание на использованный метод
(%i7) method;

3.8.3.5 Уравнения Бернулли
Уравнением Бернулли называется уравнение вида

 и
и  — функции от x или постоянные числа, а
— функции от x или постоянные числа, а  — постоянное число, не равное 0 и 13При
— постоянное число, не равное 0 и 13При  получаем неоднородное, а при
получаем неоднородное, а при  однородное линейное уравнение..
однородное линейное уравнение..Для решения уравнения Бернулли применяют подстановку  , с помощью которой, уравнение Бернулли приводится к линейному.
, с помощью которой, уравнение Бернулли приводится к линейному.
Пример решения уравнения Бернулли с помощью Maxima:
(%i1) deq:'diff(y,x)=4/x*y+x*sqrt(y);
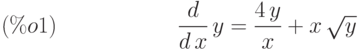
(%i2) ode2(deq,y,x);

(%i3) method;

(%i4) de1:'diff(y,x)+y/x=-x*y^2;

(%i5) ode2(de1,y,x);

3.8.3.6 Уравнения высших порядков
В Maxima при помощи функции  возможно прямое решение лишь линейных дифференциальных уравнений второго порядка При решении выполняется проверка, является ли заданное уравнение линейным, т.е. возможно ли его преобразование к форме
возможно прямое решение лишь линейных дифференциальных уравнений второго порядка При решении выполняется проверка, является ли заданное уравнение линейным, т.е. возможно ли его преобразование к форме  .
.
Первоначально отыскивается решение однородного уравнения вида 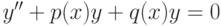 в форме
в форме  (
( — произвольные постоянные). Если
— произвольные постоянные). Если  , отыскивается частное решение неоднородного уравнения методом вариации постоянных. . .
, отыскивается частное решение неоднородного уравнения методом вариации постоянных. . .
3.8.3.7 Уравнения с постоянными коэффициентами
Решения однородных уравнений вида  отыскиваются по результатам решения характеристического уравнения
отыскиваются по результатам решения характеристического уравнения  . Возможны следующие варианты комбинаций его корней
. Возможны следующие варианты комбинаций его корней  :
:
-
 — вещественные и различные. Решение представляется в форме
— вещественные и различные. Решение представляется в форме 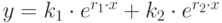 .
. -
 — корни вещественные одинаковые. Решение представляется в форме
— корни вещественные одинаковые. Решение представляется в форме 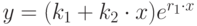 .
. -
 — комплексные (сопряжённые). Если
— комплексные (сопряжённые). Если  , то решение представляется в виде
, то решение представляется в виде 
Общее решение неоднородного уравнения с постоянными коэффициентами представляется в виде суммы общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного.
Примеры решения ОДУ второго порядка с постоянными коэффициентами:
Неоднородное уравнение общего вида:
(%i1) de1:2*'diff(y,x,2)-'diff(y,x)-y=4*x*exp(2*x);

(%i2) ode2(de1,y,x);

Частное решение неоднородного уравнения сохраняется в переменной  :
:
(%i3) yp;

Неоднородное уравнение с кратными корнями характеристического уравнения:
(%i1) de2:'diff(y,x,2)-2*'diff(y,x)+y=x*exp(x);

(%i2) ode2(de2,y,x);

(%i3) yp;

Неоднородное уравнение с комплексными корням:
(%i4) de3:'diff(y,x,2)+y=x*sin(x);

(%i5) ode2(de3,y,x);

(%i6) yp;

3.8.3.8 Уравнения с переменными коэффициентами
Аналогично уравнению с постоянными коэффициентами, общее решение однородного уравнения  имеет вид
имеет вид 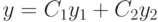 , где
, где  — линейно независимые решения однородного ОДУ (фундаментальная система решений).
— линейно независимые решения однородного ОДУ (фундаментальная система решений).
Общее решение неоднородного уравнения  с непрерывными коэффициентами и правой частью имеет вид y
с непрерывными коэффициентами и правой частью имеет вид y , где
, где  — общее решение соответствующего однородного уравнения,
— общее решение соответствующего однородного уравнения,  — частное решение неоднородного.
— частное решение неоднородного.
Если известна фундаментальная система решений однородного уравнения, общее решение неоднородного может быть представлено в форме:

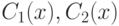 определяются методом вариации произвольных постоянных.
определяются методом вариации произвольных постоянных.Пример:
(%i3) difur:x^2*'diff(y,x,2)-x*'diff(y,x)=3*x^3;

(%i4) ode2(difur,y,x);
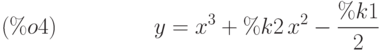
Пример:
(%i3) difur1:x*'diff(y,x,2)+'diff(y,x)=x^2;

(%i4) ode2(difur1,y,x);

3.8.3.9 Уравнение Эйлера
Однородное уравнение  называется уравнением Эйлера. Его общее решение имеет вид
называется уравнением Эйлера. Его общее решение имеет вид  , где
, где  и
и  — решения уравнения r(r _ 1) + ar + b = 0.
— решения уравнения r(r _ 1) + ar + b = 0.
В случае, когда уравнение  имеет двукратный корень
имеет двукратный корень  , решение представляется в форме
, решение представляется в форме  .
.
Неоднородное уравнение типа Эйлера сводится к однородному с постоянными коэффициентами путём соответствующей замены.
Пример:
(%i1) du:x^2*'diff(y,x,2)+x*'diff(y,x)+y=1;

(%i2) ode2(du,y,x);

3.8.3.10 Граничные задачи
Для задания граничных условий при интегрировании ОДУ второго порядка используется функция  .
.
Синтаксис вызова:  , где
, где  — значение
— значение  в первой граничной точке,
в первой граничной точке,  — значение решения
— значение решения  в той же точке (обе величины задаются в форме
в той же точке (обе величины задаются в форме  ).
).
Пример использования  и
и  :
:
(%i1) 'diff(y,x,2) + y*'diff(y,x)^3 = 0;

(%i2) ode2(%,y,x);

(%i3) bc2(%,x=0,y=1,x=1,y=3);

