Базовые положения теории многофункциональных логических модулей
5.3. Структурно-функциональная избыточность многофункциональных логических модулей и формальных нейронов
Как уже отмечалось выше, МДМ является универсальным, если реализуемое им множество функций 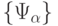 включает в себя в качестве подмножества некоторый полный класс функций типа (5.2), то есть
включает в себя в качестве подмножества некоторый полный класс функций типа (5.2), то есть 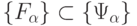 .
.
В технике обычно стремятся к тому, чтобы МДМ был не избыточен по отношению к заданному классу функций:
 |
( 5.15) |
В реальных нейронах и нейронных ансамблях функциональная избыточность значительна, то есть
 |
( 5.16) |
В формальных нейронах и, в частности, в МПЭ присутствует еще и структурная избыточность, которая обеспечивает настройку на одну и ту же ЛФ или ДФ с помощью множества варьируемых параметров модели. В частности, МПЭ можно настроить на одну и ту же 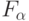 с помощью целой совокупности значений компонент весового вектора
с помощью целой совокупности значений компонент весового вектора  и вектора порогов
и вектора порогов 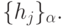
Если принять во внимание еще и физические процессы, которые лежат в основе работы УДМ или МДМ, то многообразие способов реализации одних и тех же функций становится необозримым. Но канонический характер преобразований (5.13) и (5.14) позволяет абстрагироваться от такого многообразия способов реализации, что следует из теоремы Кэли [103], которая гласит: любую конечную группу преобразований можно представить группой подстановок. Отсюда следует, что каким бы способом ни был реализован МДМ или УДМ, его работу или настройку всегда можно описать в виде (5.13) или (5.14).
Чтобы удовлетворить (5.15), необходимо иметь в виду, что перечислительный (адаптивный) процесс настройки МДМ или УДМ на требуемую функцию задан на упорядоченных определенным образом подклассах функции (5.2). В частности, можно убедиться [119], что с ростом хотя бы одного из перестраиваемых параметров ( 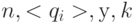 ) преобразований (5.13) каждый последующий класс
) преобразований (5.13) каждый последующий класс 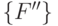 включает в себя все предыдущие, если
включает в себя все предыдущие, если  ,
, 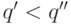 ,
,  или если любая из переменных
или если любая из переменных  имеет значность
имеет значность 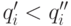 , то
, то 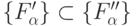 .
.
Если под элементами множества 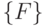 понимать полные классы
понимать полные классы 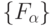 , то с ростом хотя бы одного из параметров (
, то с ростом хотя бы одного из параметров (  ,
, 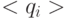 ,
, 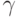 ,
,  ) эти классы образуют алгебраическую структуру [103, 120] с отношением включения классов с меньшими значениями перестраиваемых параметров в классы с большими значениями соответствующих параметров.
) эти классы образуют алгебраическую структуру [103, 120] с отношением включения классов с меньшими значениями перестраиваемых параметров в классы с большими значениями соответствующих параметров.
Для таких структур в теории групп [103] доказываются следующие утверждения:
- Всякая структура изоморфно вкладывается в структуру отношений эквивалентности, определенных в некотором множестве (теорема Уитмена).
- Структура отношений эквивалентности, определенная в произвольно заданном множестве, изоморфно вкладывается в структуру подгрупп некоторой группы (теорема Биркхофа).
Поскольку задаваемое функцией (5.2) отношение "эквизначности" является отношением эквивалентности, процесс адаптации МДМ или УДМ требует как минимум перехода от одного отношения эквивалентности к другому.
Отсюда, в соответствии с теоремой Уитмена разнообразие способов получения структуры, описывающей специфику работы конкретных УДМ, представимо структурой отношений эквивалентности, а в соответствии с теоремой Биркхофа - соотношение (5.13) описывает не только работу, но и настройку любого УДМ на  .
.
Класс двузначных ЛФ лежит в основе современной микроэлектроники, и он вырожден по отношению к классу многозначных (дискретных) функций (5.2), так как при его перечислении варьируют только количеством переменных (  ) и спецификациями
) и спецификациями 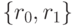 . С этим классом функций связана дистрибутивная структура, для которой справедлива теорема Стоуна [103]: для всякой дистрибутивной структуры существует мономорфизм, отображающий эту структуру во множество всех ее подмножеств и переводящий дополнение в дополнение. (Под мономорфизмом понимается однозначное отображение, при котором образы различных элементов различны.)
. С этим классом функций связана дистрибутивная структура, для которой справедлива теорема Стоуна [103]: для всякой дистрибутивной структуры существует мономорфизм, отображающий эту структуру во множество всех ее подмножеств и переводящий дополнение в дополнение. (Под мономорфизмом понимается однозначное отображение, при котором образы различных элементов различны.)
Теорема Стоуна показывает, что для построения двузначных УДМ необходимо получить (с помощью  и
и  ) множество всевозможных подмножеств входных векторов
) множество всевозможных подмножеств входных векторов  , а с помощью преобразования
, а с помощью преобразования  разместить значения ЛФ ("ноль" и "единица") соответственно над подмножеством
разместить значения ЛФ ("ноль" и "единица") соответственно над подмножеством 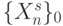 и его дополнением
и его дополнением 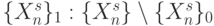 .
.
В сравнении с теоремой Шеннона [101] теорема Стоуна предоставляет более широкий выбор способов построения УДМ, так как она сформулирована в терминах теории множеств и не предполагает какой-либо фиксированной формы логической записи и реализации 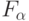 , что наглядно иллюстрирует МПЭ [79, 80], где входные преобразования носят чисто арифметический, а не логический характер.
, что наглядно иллюстрирует МПЭ [79, 80], где входные преобразования носят чисто арифметический, а не логический характер.
В технических системах функциональная избыточность УДМ "дозируется" соображениями экономичности, отказоустойчивости и надежности, когда требование минимума аппаратурных затрат на реализацию и управление УДМ необходимо совместить с требованием повышенной устойчивости к (частичным) отказам объекта и средств адаптации УДМ.
На абстрактном уровне структурно-функциональную избыточность УДМ можно оценить отношением мощности множества всевозможных состояний вектора управления 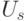 к мощности класса реализуемых функций:
к мощности класса реализуемых функций:
 |
( 5.17) |
где  - оценивается при независимом управлении параметрами настройки входного преобразования
- оценивается при независимом управлении параметрами настройки входного преобразования 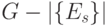 , внутреннего преобразования
, внутреннего преобразования 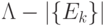 , и выходного преобразования
, и выходного преобразования  , а
, а  .
.
Ограничение снизу в (5.17) показывает, что на любую функцию  можно настроиться хотя бы одним способом, то есть при неизбыточном управлении мощность множества состояний вектора управления
можно настроиться хотя бы одним способом, то есть при неизбыточном управлении мощность множества состояний вектора управления 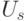 равна мощности множества реализуемых функций.
равна мощности множества реализуемых функций.
Ограничение "сверху" в (5.17) можно получить, считая: 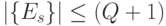 !;
!; 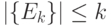 !;
!;  - мощность множества всевозможных
- мощность множества всевозможных  -разбиений числа (
-разбиений числа ( 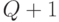 ).
).
Тогда:
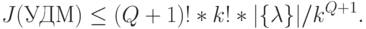 |
( 5.18) |
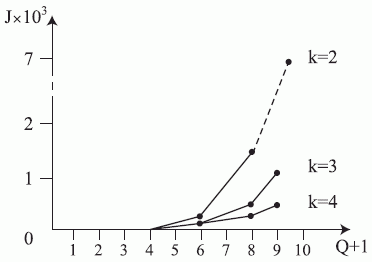
В табл. 5.3 приведены численные оценки (5.18), показывающие характер изменения структурно-функциональной избыточности УДМ в зависимости от параметров его настройки на 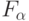 из заданного класса
из заданного класса 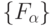 . Из табл. 5.3 видно, что с ростом
. Из табл. 5.3 видно, что с ростом  (при фиксированных
(при фиксированных  - рис. 5.5) структурно-функциональная избыточность УДМ резко возрастает, а с ростом
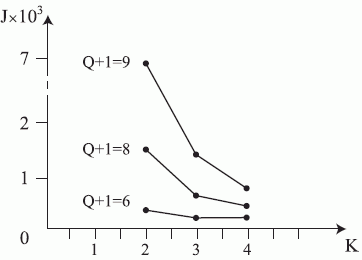
- рис. 5.5) структурно-функциональная избыточность УДМ резко возрастает, а с ростом  (при фиксированных
(при фиксированных  - рис. 5.6) - падает.
- рис. 5.6) - падает.
 | ||||
|---|---|---|---|---|
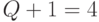 |
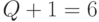 |
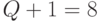 |
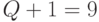 |
|
 |
9 | 90 | 1575 | 7087 |
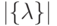 |
3 | 4 | 5 | 5 |
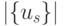 |
144 | 5760 | 403200 | 3628800 |
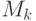 |
16 | 64 | 256 | 522 |
 | ||||
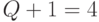 |
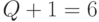 |
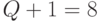 |
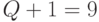 |
|
 |
7 | 41 | 368 | 1322 |
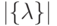 |
4 | 7 | 10 | 12 |
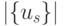 |
576 | 30240 | 2419200 | 26127360 |
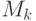 |
81 | 249 | 6561 | 19683 |
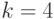 | ||||
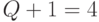 |
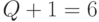 |
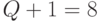 |
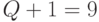 |
|
 |
11 | 38 | 221 | 533 |
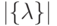 |
5 | 9 | 15 | 17 |
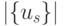 |
2880 | 155520 | 14515200 | 140797660 |
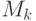 |
256 | 4096 | 65536 | 262144 |
Отсюда следует практическая рекомендация по нахождению минимально избыточных в смысле (5.17) и (5.18) УДМ: необходимо максимально упрощать входное преобразование и максимально использовать возможности выходного преобразования канонической тройки (5.13), особенно при реализации ЛФ, где  .
.
Таким условиям удовлетворяет УДМ, в котором  и
и  фиксированы, а все адаптивные возможности сосредоточены в выходном контуре:
фиксированы, а все адаптивные возможности сосредоточены в выходном контуре:
 |
( 5.19) |
где оператор  разбивает все множество
разбивает все множество  на (
на ( 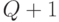 ) одноэлементных подмножеств, а выходное преобразование
) одноэлементных подмножеств, а выходное преобразование 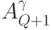 размещает с повторениями
размещает с повторениями 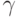 значений
значений 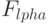 над (
над ( 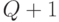 ) одноэлементными подмножествами.
) одноэлементными подмножествами.
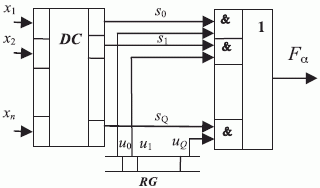
Требованиям (5.19) отвечает УДМ, который включает (рис. 5.7):
- неперестраиваемый дешифратор (DC), реализующий оператор
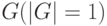 ,
, - селектор-мультиплексор (MS), реализующий фиксированное
 -разбиение (
-разбиение ( 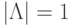 ),
), - (
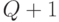 )-разрядный регистр (RG), выполняющий подстановку
)-разрядный регистр (RG), выполняющий подстановку 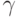 значений
значений 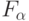 над (
над ( 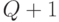 ) элементом
) элементом 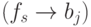 .
.
Настройка УДМ рис. 5.7 на 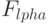 выполняется загрузкой в регистр RG управляющего вектора
выполняется загрузкой в регистр RG управляющего вектора 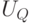 , представляющего собой
, представляющего собой  -значный код числа
-значный код числа  .
.
Взаимно однозначное отображение  зависит от правил объединения на входах селектора MS
зависит от правил объединения на входах селектора MS  -выходов дешифратора DC и
-выходов дешифратора DC и 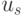 -выходов регистра настройки RG. Например, тривиальная
-выходов регистра настройки RG. Например, тривиальная  -нумерация двумерных двузначных ЛФ задается таблицей 5.4, и она всегда будет подразумеваться в дальнейшем, если не оговорено иное.
-нумерация двумерных двузначных ЛФ задается таблицей 5.4, и она всегда будет подразумеваться в дальнейшем, если не оговорено иное.
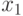 |
 |
 |
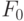 |
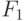 |
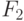 |
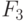 |
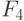 |
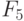 |
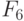 |
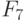 |
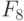 |
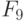 |
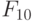 |
 |
 |
 |
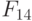 |
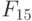 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
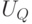 |
 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
 |
0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | ||
 |
0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | ||
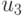 |
0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ||
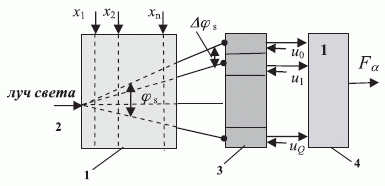
В оптоэлектронике оператор линейной свертки можно реализовать не на схемотехническом, а на физико-техническом уровне работы ней-роподобной элементной базы, что резко снижает аппаратные затраты на МПЭ по сравнению с дискретными схемами. В оптоэлектронном МПЭ рис. 5.8 [122] использована схема (5.19), где:
- дешифратор DC выполнен в виде волоконно-оптической системы 1, которая отклоняет луч 2 инжекционного лазера по закону
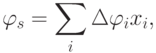
где
 -двоичные переменные, связанные с наличием ("логическая единица") или отсутствием ("логический ноль") электрического тока в металлизированных волокнах - входах оптоэлектронного УДМ;
-двоичные переменные, связанные с наличием ("логическая единица") или отсутствием ("логический ноль") электрического тока в металлизированных волокнах - входах оптоэлектронного УДМ; 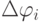 - "локальный" угол отклонения луча от горизонтальной оси, причем если
- "локальный" угол отклонения луча от горизонтальной оси, причем если 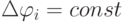 (по
(по  ), то УДМ является мажоритарным, а если
), то УДМ является мажоритарным, а если 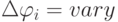 (по
(по  ), то УДМ является многопороговым;
), то УДМ является многопороговым; - селектор MS реализован в виде оптоэлектронного транспаранта 3;
- "плоский" регистр RG реализован в виде памяти связей, которая формирует выходное значение
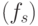 оптоэлектронного УДМ в соответствии со значением управляющего потенциала
оптоэлектронного УДМ в соответствии со значением управляющего потенциала 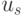 того элемента транспаранта, на который падает в данный момент луч лазера.
того элемента транспаранта, на который падает в данный момент луч лазера.
В теории многофункциональных логических модулей [101] все рассмотренные УДМ считаются выполненными по схеме с раздельными информационными (  ) и управляющими (
) и управляющими (  ) входами. На практике применяются и схемы со смешанными информационными и управляющими входами, адаптация которых выполняется с помощью преобразований:
) входами. На практике применяются и схемы со смешанными информационными и управляющими входами, адаптация которых выполняется с помощью преобразований:
-
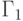 - перестановка переменных
- перестановка переменных  по входам
по входам 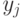 МДМ (
МДМ ( 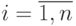 ;
; 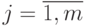 ;
;  );
); -
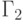 - инверсия переменных
- инверсия переменных  ;
; -
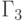 - фиксация значений отдельных входов (
- фиксация значений отдельных входов ( 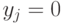 или
или 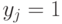 );
); -
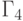 - отождествление отдельных входов, то есть подача одной и той же переменной
- отождествление отдельных входов, то есть подача одной и той же переменной  на произвольное подмножество входов
на произвольное подмножество входов 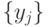 .
.
Вне зависимости от значности входных переменных их перестановки по (  ) и инверсии образуют группу переименований переменных [86, 123] порядка
) и инверсии образуют группу переименований переменных [86, 123] порядка  !, которая является подгруппой
!, которая является подгруппой  , имеющей порядок
, имеющей порядок 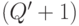 !, где
!, где 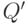 определена на множестве
определена на множестве 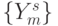 .
.
Фиксация и отождествление переменных не выводят за класс функций 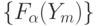 , к которому принадлежит реализуемая МДМ первообразная [101] функция
, к которому принадлежит реализуемая МДМ первообразная [101] функция  , такая, что
, такая, что ![F_{\alpha}^{*}[\Gamma(Y_m)] = \{F_{\alpha}(X^{s}_n)\}](/sites/default/files/tex_cache/169a379fd083c15416248b1ee895623c.png) , где
, где 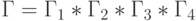 .
Поэтому, выбрав в (5.2) параметры класса функций
.
Поэтому, выбрав в (5.2) параметры класса функций 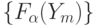 , можно с помощью канонической системы преобразований описать работу и адаптацию МДМ со смешанными информационными и управляющими входами.
, можно с помощью канонической системы преобразований описать работу и адаптацию МДМ со смешанными информационными и управляющими входами.
Таким образом, на основе преобразований, сохраняющих отношение эквизначности, удалось:
- Построить каноническую систему преобразований универсальных дискретных модулей, которая пригодна как для описания собственно вычислительного процесса, так и для перечисления всех арифметико-логических инструкций, используемых в программе.
- Оценить структурно-функциональную избыточность канонической системы преобразований УДМ и построить его минимально избыточную схему.
- Показать инвариантность канонической системы преобразований способам адаптации наиболее распространенных в технике УДМ с раздельными и смешанными информационными и управляющими входами.
- Расширить сферу поиска физических процессов под перспективные вычислительные элементы и схемы, так как каноническая система преобразований оперирует не понятиями булевой алгебры, а понятиями теории групп, длительное время обслуживающей нужды физиков и химиков.