Базовые положения теории многофункциональных логических модулей
5.1. Методы структурно-параметрической адаптации многофункциональных логических модулей
Одна из центральных проблем построения (Б)ВС на основе "большого" (  ) количества вычислителей состоит в поиске эффективных методов и средств управления и координации работы всего коллектива и каждого его члена [104-106]. К сожалению, теория многофункциональных дискретных модулей (МДМ) [68, 71, 101, 107, 108] основное внимание сконцентрировала на оценке функциональных возможностей, анализе и синтезе схем из МДМ, а теория адаптивных систем [109-111] основное внимание уделяет исследованию сходимости и эффекти
вности алгоритмов оптимизации. В связи с этим, прежде всего рассмотрим суть
процесса адаптации МДМ и ответим на вопрос: что происходит в процессе управления дискретным объектом? Покажем на ряде примеров, что адаптация непрерывных и дискретных объектов представляет собой процесс устранения, а в общем виде ослабления неоднозначности в отображении "вход-выход", реализуемом объектом адаптации.
) количества вычислителей состоит в поиске эффективных методов и средств управления и координации работы всего коллектива и каждого его члена [104-106]. К сожалению, теория многофункциональных дискретных модулей (МДМ) [68, 71, 101, 107, 108] основное внимание сконцентрировала на оценке функциональных возможностей, анализе и синтезе схем из МДМ, а теория адаптивных систем [109-111] основное внимание уделяет исследованию сходимости и эффекти
вности алгоритмов оптимизации. В связи с этим, прежде всего рассмотрим суть
процесса адаптации МДМ и ответим на вопрос: что происходит в процессе управления дискретным объектом? Покажем на ряде примеров, что адаптация непрерывных и дискретных объектов представляет собой процесс устранения, а в общем виде ослабления неоднозначности в отображении "вход-выход", реализуемом объектом адаптации.
Адаптация в живой природе прежде всего предполагает устранение (ослабление) неоднозначности реакции организма на повторяющиеся события внешнего мира [25]. В частности, при выработке условных рефлексов у животных и человека устанавливается однозначное соответствие между опережающим стимулом и последующей реакцией, в формировании которого участвует сложная функциональная система, создаваемая организмом для достижения полезного приспособительного эффекта в конкретных метастабильных условиях внешней среды (см. раздел 4.3). Поэтому можно сказать, что при выработке условных рефлексов и других более сложных устойчивых форм поведения [25, 112] организм выбирает из множества входных воздействий наиболее информативные и "устойчивые" и ставит им в соответствие наиболее адекватные и достаточно однозначные для данных условий проведения поведенческих актов.
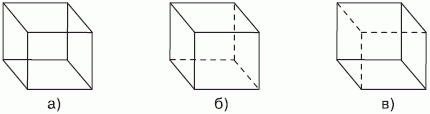
Неоднозначность в живых системах устраняется (ослабляется) начиная с сенсорного уровня, то есть в процессе активного восприятия [113] звуковых, зрительных, тепловых и т. п. сигналов и образов. Заимствованный из [32] рис. 5.1 иллюстрирует: до задания пунктирных линий (рис. 5.1-а) допускается двойственное восприятие пространственного положения куба (рис. 5.1-б и 5.1-в).
В моделях формальных нейронов и в перцептронах [68, 71, 108] проблема устранения неоднозначности при переходе от реальных к формальным переменным не стоит, так как в технических системах "восприятие" осуществляется через датчики, которые работают с ограниченной точностью, чувствительностью и при наличии внутренних и внешних шумов. Поэтому датчик, как и любая измерительная система, ставит в соответствие множеству входных воздействий  множество выходных реакций
множество выходных реакций  , а неоднозначность, как правило, устраняется усреднением значений по этим множествам. В результате вместо отображения
, а неоднозначность, как правило, устраняется усреднением значений по этим множествам. В результате вместо отображения 
 используется отображение
используется отображение  ,где
,где  ,
,  - соответствующие средние.
- соответствующие средние.
В вычислительной технике до задания управляющих воздействий на операционное устройство также невозможно говорить об однозначном соответствии между его информационными входами и выходом. Однако здесь картина размывается тем обстоятельством, что разработчики МДМ принимают специальные схемотехнические меры, исключающие "неоднозначные" состояния. Тем не менее и в этом случае отказы и неисправности приводят к неоднозначным отображениям типа "вход-выход". Поэтому имеются достаточные основания рассматривать адаптацию широкого класса технических и биологических систем как процесс устранения (ослабления) неоднозначности в выполняемых ими отображениях "вход-выход".
Определим типы преобразований, которые лежат в основе моделей адаптивных процессов такого типа.
Из приведенных примеров видно, что существует большое разнообразие способов и приемов устранения или хотя бы ослабления неоднозначности. В классических адаптивных [110, 111] и кибернетических системах [14, 17, 72, 114] неоднозначность преимущественно устраняется на основе метрических соотношений. Поэтому в моделях таких систем используются метрически транзитивные преобразования, то есть преобразования, сохраняющие меру [14]. При управлении дискретными системами функциональная устойчивость уже зависит не столько от метрических соотношений во входных воздействиях и реализуемых преобразованиях, сколько от сохранения отношения эквивалентности, так как реакция таких систем определяется принадлежностью каждого входного воз действия некоторому подмножеству, однозначно связанному со значением алфавита выходной реакции системы.
Наиболее четко отмеченная разница между моделями непрерывных и дискретных систем проявилась при исследовании перцептронов [108, 110] и многопороговых элементов (МПЭ) [78-80, 115], которые были одними из первых технически реализованных нейроподобных элементов.
Воспользуемся импликативной формой записи МПЭ раздела 4.6:
![L(X^{s}_{n},W_n):X^{s}_{n} \to(l_{s}(X^s_n,W_{n}) =
\sum_{i=1}^{n}{x_i^s*w_{i}}) \in (h_{j-l},h_j]\Rightarrow f_{s}:= b_j, (5.1)](/sites/default/files/tex_cache/1989f8176f0bb3d13db4fc401e2fc859.png) |
( 5.1) |
где:
-
 - оператор линейной свертки компонент входного вектора
- оператор линейной свертки компонент входного вектора 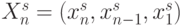 (заданы на целочисленной решетке
(заданы на целочисленной решетке  ,
, 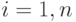 ;
;  ;
;  ;
; 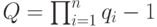 ;)
и компонент весового вектора
;)
и компонент весового вектора 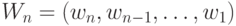 ,
, 
-
 - вектор порогов размерности у, компоненты которого разбивают скалярную ось
- вектор порогов размерности у, компоненты которого разбивают скалярную ось 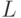 на
на 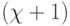 пороговых полуинтервалов
(
пороговых полуинтервалов
( ![(h_{j-1},h]](/sites/default/files/tex_cache/597156bfa18109baacd15bb4fa6532b0.png) ,
,  ;
;  );
); - реализуемая МПЭ произвольнозначная логическая функция (ЛФ) имеет вид:
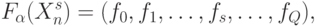
( 5.2) у которой:
 ,
,  ,
, 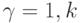 ;
;  ;
; 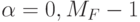 .
.
Соотношение (5.2) задает не только произвольнозначную ЛФ, но и произвольную дискретную функцию (ДФ), полностью определенную на всех  -наборах входных переменных, причем мощность
-наборах входных переменных, причем мощность  множества значений каждой входной переменной может быть произвольной. При равнозначных входных переменных
множества значений каждой входной переменной может быть произвольной. При равнозначных входных переменных  мощность множества входных векторов
мощность множества входных векторов  , мощность множества
, мощность множества  -значных ЛФ (или ДФ)
-значных ЛФ (или ДФ)  , а при
, а при 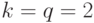 имеем класс
имеем класс  -мерных булевых функций мощности
-мерных булевых функций мощности 
Это говорит о применимости (5.1) как на макроуровне при описании систем распознавания образов (перцептронный подход), так и на микроуровне при описании работы МПЭ.
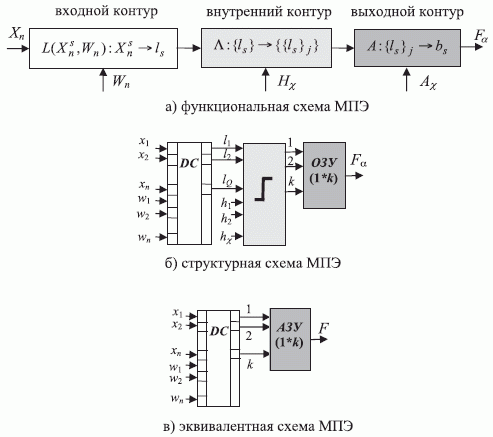
Отвечающая (5.1) функциональная схема МПЭ включает (рис. 5.2-а):
- входной преобразователь
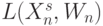 , где реализуется отображение
вектора
, где реализуется отображение
вектора  на скалярную ось
на скалярную ось 
- внутренний преобразователь
 , где реализуется разбиение всего множества значений свертки
, где реализуется разбиение всего множества значений свертки  на
на  подмножеств, таких,
подмножеств, таких, 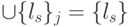 ;
; 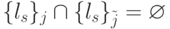 при
при  и
и 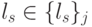 , если
, если 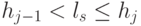 (здесь
(здесь  - "пустое" множество, а объединение -
- "пустое" множество, а объединение -  и пересечение -
и пересечение -  подмножеств берутся по индексу
подмножеств берутся по индексу  );
); - выходной преобразователь, где реализуется размещение (возможно и с повторениями)
 значений ЛФ над
значений ЛФ над 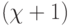 пороговым полуинтервалом:
пороговым полуинтервалом:  .
.
В разделе 4.6 проанализированы условия эквивалентного перехода от МПЭ с аналоговыми параметрами ( 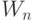 и
и  ) к МПЭ с дискретными параметрами и показано, что перестройка входного преобразования МПЭ связана с вариациями
) к МПЭ с дискретными параметрами и показано, что перестройка входного преобразования МПЭ связана с вариациями  весового вектора и приводит к различным
весового вектора и приводит к различным 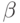 -перестановкам упорядоченных компонент свертки на скалярной оси
-перестановкам упорядоченных компонент свертки на скалярной оси  . В результате полная вариация весового вектора
. В результате полная вариация весового вектора 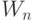 порождает множество
порождает множество  перестановок значений компонент свертки и связанных с ними индексов
перестановок значений компонент свертки и связанных с ними индексов  , которое разбивает все пространство
, которое разбивает все пространство 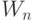 на классы эквивалентности (индексные зоны - ИЗ)
на классы эквивалентности (индексные зоны - ИЗ)  , такие, что вариации внутри класса
, такие, что вариации внутри класса  , не нарушают связанного с этим классом отношения порядка между значениями свертки.
, не нарушают связанного с этим классом отношения порядка между значениями свертки.
Такая дискретизация непрерывного пространства 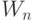 позволяет представить (рис. 5.2-б) входной преобразователь
позволяет представить (рис. 5.2-б) входной преобразователь 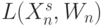 полным, перестраиваемым по
полным, перестраиваемым по 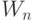 дешифратором входных сигналов
дешифратором входных сигналов  , внутренний преобразователь
, внутренний преобразователь  - многоуровневым (перестраиваемым по
- многоуровневым (перестраиваемым по  ) компаратором, выходы которого адресуют ячейки памяти, где хранятся соответствующие значения ЛФ (или ДФ)
) компаратором, выходы которого адресуют ячейки памяти, где хранятся соответствующие значения ЛФ (или ДФ)  .
.
Если в качестве памяти выбрать ОЗУ произвольной выборки, а полный дешифратор и компаратор заменить эквивалентным "стягивающим" дешифратором, то получим (рис. 5.2-в) типичную схему ассоциативного ЗУ (АЗУ), адресуемого содержимым  [46, 116].
[46, 116].
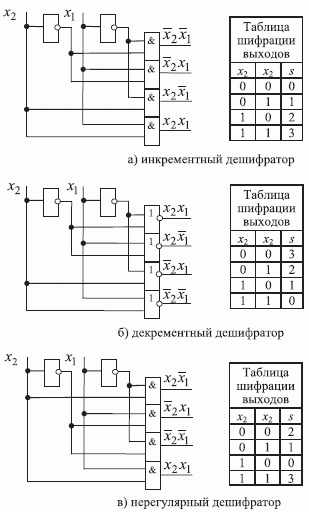
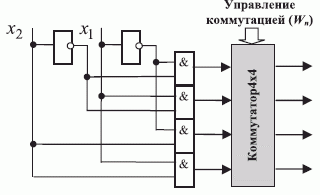
Дискретные дешифраторы можно перестраивать как структурно (рис. 5.3), так и параметрически (рис. 5.4). В первом случае добиться требуемой реакции дешифратора можно как заменой базисных элементов, так и модификацией схемы их соединения, то есть модификацией самой схемы. Во втором случае схема дешифратора остается неизменной, но в нее необходимо ввести полный коммутатор, а управление законом коммутации осуществлять с помощью двоичного вектора 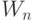 .
.
В любом случае для устойчивой реализации заданной функции 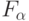 вида (5.2) как минимум необходимо сохранить отношение порядка (при фиксированном правиле разбиения в непрерывном случае
вида (5.2) как минимум необходимо сохранить отношение порядка (при фиксированном правиле разбиения в непрерывном случае  и правиле подстановки
и правиле подстановки  и дискретном случае
и дискретном случае 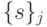 и
и 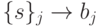 соответственно).
соответственно).
Напротив, при перестройке МПЭ с одной функции на другую необходимо:
- либо перейти в другую ИЗ, изменив тем самым отношение порядка между значениями компонент свертки
 ,
, - либо изменить правила разбиения упорядоченного множества значений свертки
 на подмножества
на подмножества 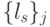 ,
, - либо модифицировать правила подстановки

Отсюда, в классических МПЭ фактически используется три типа преобразований, которые инвариантны непрерывному или дискретному характеру изменения значений реализуемых аргументов и функций: перестановки входных векторов или их скалярных "представителей", разбиения множества значений входных векторов или их "скалярных представителей" на классы эквивалентности и подстановки значений заданной функции над классами эквивалентности. Поэтому специфика адаптации дискретных систем состоит в том, что в них неоднозначность в отображении "вход-выход" устраняется не на основе преобразований, сохраняющих меру, как это имеет место в классических кибернетических системах, а на основе преобразований, сохраняющих отношение, которое задает на множестве значений своих аргументов реализуемая объектом адаптации функция.
Определим взаимоотношение двух классов преобразований: сохраняющих меру и сохраняющих отношение, и на этой основе покажем, что методы управления непрерывными адаптивными системами не всегда пригодны для управления дискретными адаптивными системами.
Из элементарной алгебры известно:
- Знак неравенства не изменится, если обе его части умножить на одно и то же положительное число (масштабирование).
- Знак неравенства не изменится, если к обеим его частям прибавить одно и то же число (линейный сдвиг). Свойством сохранения порядка обладают и нелинейные преобразования.
- Два неравенства одного и того же знака можно складывать почленно, отчего знак неравенства не изменится (нелинейный сдвиг). Покажем справедливость утверждения 5.1: множество преобразований, сохраняющих меру и сохраняющих отношение, пересекаются только частично.
Пусть задано конечномерное пространство  векторов
векторов  , определенных в (5.1). Функция
, определенных в (5.1). Функция 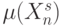 называется мерой, если [117]:
называется мерой, если [117]:
- область ее определения является полукольцом множеств
 ;
; - значения функции действительны и положительны;
- эта функция аддитивна, то есть для любого разбиения
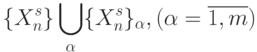
выполняется равенство
 , где
, где 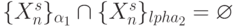 при
при 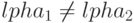 .
.
Здесь символами  ,
,  ,
,  обозначены соответственно множество "пусто", теоретико-множественное объединение и пересечение.
обозначены соответственно множество "пусто", теоретико-множественное объединение и пересечение.
Квадратом 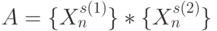 называется множество упорядоченных пар
называется множество упорядоченных пар  , где
, где  и
и  . Пусть
. Пусть  - подмножество квадрата (
- подмножество квадрата ( 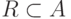 ). Тогда говорят, что элемент
). Тогда говорят, что элемент 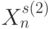 находится в отношении
находится в отношении  к элементу
к элементу 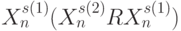 , если пара
, если пара  .
.
Из определения меры и отношения следует, что их можно задать на одном и том же векторном пространстве одновременно и независимо друг от друга.
Для определенности будем считать:
 |
( 5.3) |
где  - абсолютное значение длины вектора
- абсолютное значение длины вектора  ;
;
 |
( 5.4) |
где 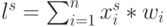 и
и 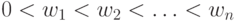 .
.
Говорят, что преобразование  сохраняет меру
сохраняет меру  , если
, если ![\mu[Ф(X_n^{s})] = \mu(\{X_{n}^{s}\})](/sites/default/files/tex_cache/f9b6989407fe83d5053eddc7f2deebc7.png) , а преобразование
, а преобразование  сохраняет отношение
сохраняет отношение  , если
, если ![[Ф'(X_{n}^{s(2)})]R [Ф'(X_{n}^{s(1)})] \sim X_{n}^{s(2)} R X_n^{s(1)}](/sites/default/files/tex_cache/97b1045aed5940d2907933da3ad78449.png) , где
, где 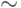 - отношение эквивалентности.
- отношение эквивалентности.
Обозначим через 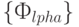 множество всевозможных преобразований, заданных на
множество всевозможных преобразований, заданных на  . Индексами
. Индексами  ,
,  ,
,  ,
,  ,
,  отметим подмножества
отметим подмножества  , которые сохраняют соответственно меру, отношение, и меру и отношение, только меру, только отношение.
, которые сохраняют соответственно меру, отношение, и меру и отношение, только меру, только отношение.
Для доказательства сформулированного утверждения достаточно показать, что каждое из подмножеств 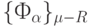 ,
,  и
и 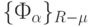 - "не пусто".
- "не пусто".
- Из аддитивного свойства меры следует, что она инвариантна перестановкам векторов
 по индексу
по индексу  , которые не нарушают фиксированного разбиения
, которые не нарушают фиксированного разбиения  Поэтому если
Поэтому если  - отношение порядка типа (5.4), а
- отношение порядка типа (5.4), а  - множество перенумераций индексов
- множество перенумераций индексов  !, то любое
!, то любое  сохраняет меру
сохраняет меру  , но не отношение порядка типа (5.4) (кроме, естественно, тождественной перестановки индексов
, но не отношение порядка типа (5.4) (кроме, естественно, тождественной перестановки индексов  ).
). - Из аддитивного свойства меры и второго свойства неравенств следует, что линейные сдвиги задают множество преобразований
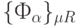 , сохраняющих и меру и отношение.
, сохраняющих и меру и отношение. - Из первого свойства неравенств следует, что даже линейное
(
 ) масштабирование
) масштабирование 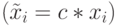 нарушает меру (5.3), но сохраняет отношение.
нарушает меру (5.3), но сохраняет отношение.
Таким образом, показано:
- Чтобы настроить МПЭ на заданную функцию, необходимо с помощью управляющих векторов устранить неоднозначность в выполняемом им отображении "вход-выход".
- Устойчивость работы МПЭ можно обеспечить, если выполняемые им преобразования сохраняют отношение эквивалентности
 , задаваемое реализуемой логической или дискретной функцией (
, задаваемое реализуемой логической или дискретной функцией (  ).
). - Множества преобразований, сохраняющих меру и сохраняющих отношение, пересекаются только частично, и поэтому методы адаптации систем с непрерывными переменными и/или параметрами нельзя автоматически распространить на дискретные адаптивные системы.
- Адаптация МПЭ (его настройка на заданную логическую или дискретную функцию, задающую отображение
 ), предполагает некоторую процедуру перечисления
), предполагает некоторую процедуру перечисления  .
.