|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Сокращение диагностической информации с использованием хеш-функций
Для оценки эффективности сокращения ДИ с помощью хеш-функций авторами работы [1]
был проведен ряд экспериментов. В процессе выполнения экспериментов подбиралась каждая из разновидностей хеш-функции для каждого варианта ДИ.
Для каждого из значений  , начиная с
, начиная с  , делалось несколько попыток подбора соответствующего параметра
, делалось несколько попыток подбора соответствующего параметра  .
При обнаружении хеш-функции, удовлетворяющей условию (34.1), процесс поиска прекращался. Вся процедура повторялась для одних и тех же устройств несколько раз, после чего вычислялись средние значения результатов.
.
При обнаружении хеш-функции, удовлетворяющей условию (34.1), процесс поиска прекращался. Вся процедура повторялась для одних и тех же устройств несколько раз, после чего вычислялись средние значения результатов.
В первой серии экспериментов производился поиск хеш-функций для исходных данных, сгенерированных случайным образом. Генерация ДИ проводилась в предположении, что полная реакция любой неисправной модификации ДУ отличается от эталонной реакции не более чем на 5%. Такая модель была выбрана в связи с тем, что одиночные неисправности в ДУ обычно приводят к незначительным изменениям реакций ДУ. Объем полной реакции варьировался от 38 до 5028 бит, а количество технических состояний было взято равным 600. Для каждого из значений  , начиная с
, начиная с  , проводилось 100 попыток подбора значения параметра
, проводилось 100 попыток подбора значения параметра  для каждого вида рассматриваемых хеш-функций. В табл. 34.2 приведены результаты этой серии экспериментов для случайных данных.
для каждого вида рассматриваемых хеш-функций. В табл. 34.2 приведены результаты этой серии экспериментов для случайных данных.
 |
 |
Вероятность нахождения 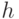 , % , % |
 |
Доля вариантов ДИ | ||||
|---|---|---|---|---|---|---|---|---|
 |
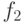 |
 |
 |
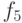 |
||||
| 15 | 0.6667 | 0.40148 | 1200 | 17.34% | 0.04% | 33.02% | 28.74% | 17.6% |
| 16 | 0.6250 | 6.39021 | 70 | 79.5% | 2.78% | 66.68% | 70.94% | 78.32% |
| 17 | 0.5882 | 25.33211 | 16 | 3.16% | 97.18% | 0.3% | 0.32% | 4.08% |
Последние пять столбцов этой таблицы показывают долю вариантов ДИ, для которых была найдена хеш-функция  ,
, 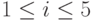 , с эффективностью сжатия
, с эффективностью сжатия  , приведенной во втором столбце. Третий и четвертый столбцы показывают, соответственно, значение вероятности (34.6) нахождения такой хеш-функции и необходимое количество
, приведенной во втором столбце. Третий и четвертый столбцы показывают, соответственно, значение вероятности (34.6) нахождения такой хеш-функции и необходимое количество  шагов для получения такой хеш-функции с вероятностью 99%. Из таблицы видно, что хеширование позволяет добиться сокращения исходной информации до размеров, всего лишь на несколько бит превосходящих оптимальный. В табл. 34.3 приводятся результаты тех же экспериментов, но с несколько другой точки зрения. Эта таблица показывает, что средняя эффективность сжатия ДИ с помощью найденной хеш-функций не зависит от длины полной реакции ДУ.
шагов для получения такой хеш-функции с вероятностью 99%. Из таблицы видно, что хеширование позволяет добиться сокращения исходной информации до размеров, всего лишь на несколько бит превосходящих оптимальный. В табл. 34.3 приводятся результаты тех же экспериментов, но с несколько другой точки зрения. Эта таблица показывает, что средняя эффективность сжатия ДИ с помощью найденной хеш-функций не зависит от длины полной реакции ДУ.
| Объем полной реакции, бит | Среднее значение 
|
||||
|---|---|---|---|---|---|
 |
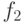 |
 |
 |
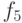 |
|
| 38-1028 | 0.63063 | 0.58897 | 0.63872 | 0.63672 | 0.63185 |
| 1038-2028 | 0.63116 | 0.58934 | 0.63835 | 0.63726 | 0.63217 |
| 2038-3028 | 0.63157 | 0.59005 | 0.63972 | 0.63786 | 0.63102 |
| 3038-4028 | 0.63197 | 0.58904 | 0.63732 | 0.63748 | 0.63091 |
| 4038-5028 | 0.62999 | 0.58904 | 0.63914 | 0.63497 | 0.62821 |
Средняя эффективность сжатия с помощью хеш-функций приведена в табл. 34.4.
Если судить по результатам этой таблицы, то наиболее привлекательными являются хеш-функции, порожденные сигнатурными анализаторами (34.3) и (34.4).
Первая серия экспериментов также показала, что поиск позиционной хеш-функции происходит медленнее, чем поиск любой другой рассматриваемой хеш-функции. Так, в проведенных экспериментах позиционная хеш-функция осуществляет наиболее эффективное сокращение ДИ лишь в 0.06% случаев, тогда как наихудший результат сжатия с использованием этой функции этой функции получен более чем в 90% случаев.
Для последующих серий экспериментов была использована ДИ, полученная для ДУ из каталога ISCAS'89 при моделировании одиночных неисправностей с помощью тестовых последовательностей HITEC. С параметрами данной ДИ можно ознакомиться в табл. 33.1.
В ходе следующей серии экспериментов для каждого варианта ДИ десять раз проводился цикл поиска рассматриваемых хеш-функций. В цикле поиска одной хеш-функции для каждого из значений  , начиная с
, начиная с  , проводилось 10 попыток подбора значения параметра
, проводилось 10 попыток подбора значения параметра  . Таким образом, по сравнению с предыдущими экспериментами, количество попыток подбора значений параметра
. Таким образом, по сравнению с предыдущими экспериментами, количество попыток подбора значений параметра  было значительно сокращено. Средние значения результатов экспериментов приведены в табл. 34.5- 34.9.
было значительно сокращено. Средние значения результатов экспериментов приведены в табл. 34.5- 34.9.
| ДУ | 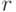 |
 |
Объем сокращенной ДИ, бит | Доля сокращенной ДИ от полной ДИ | Время подбора  , мс , мс |
|---|---|---|---|---|---|
| S298 | 13.4 | 0.60103 | 2385.2 | 0.69% | 38.46 |
| S344 | 14.3 | 0.56000 | 3446.3 | 1.02% | 36.15 |
| S349 | 14.5 | 0.55286 | 3538.0 | 0.98% | 44.67 |
| S382 | 14.1 | 0.57011 | 2693.1 | 0.11% | 290.22 |
| S386 | 14.9 | 0.60655 | 4097.5 | 0.74% | 62.97 |
| S400 | 14.1 | 0.56879 | 2749.5 | 0.11% | 260.49 |
| S444 | 14.1 | 0.56938 | 2707.2 | 0.10% | 297.57 |
| S526 | 13.6 | 0.59092 | 1890.4 | 0.10% | 230.04 |
| S641 | 15.2 | 0.59250 | 5259.2 | 0.30% | 208.47 |
| S713 | 15.5 | 0.58169 | 5332.0 | 0.39% | 225.84 |
| S820 | 17.4 | 0.57592 | 12406.2 | 0.08% | 4142.94 |
| S832 | 17.3 | 0.57884 | 12456.0 | 0.08% | 4676.4 |
| S1423 | 14.6 | 0.61887 | 4292.4 | 1.95% | 22.14 |
| S1488 | 19.3 | 0.57058 | 26248.0 | 0.09% | 12349.89 |
| S1494 | 19.5 | 0.56480 | 26539.5 | 0.08% | 13955.55 |
| S2081 | 10.1 | 0.59576 | 565.6 | 10.10% | 0.69 |
В табл. 34.5. приведены результаты сокращения ДИ с помощью полиномиальной хеш-функций.
Проведенные эксперименты показали, что эффективность сжатия ДИ для реальных ДУ с использованием хеш-функций не уступает результатам, полученным для случайных данных.
Сравнение полученных средних значений эффективности сжатия, приведенных в третьем столбце таблиц (34.5)-(34.9) подтверждает тот факт, что поиск позиционной хеш-функции происходит медленнее, т. е. за большее число итераций перебора. Кроме этого, из табл. 34.9 можно судить о нестабильности поиска хеш-функции, порожденной второй разновидностью многовходного сигнатурного анализатора.
| ДУ | 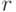 |
 |
Объем сокращенной ДИ, бит | Доля сокращенной ДИ от полной ДИ | Время подбора  , мс , мс |
|---|---|---|---|---|---|
| S298 | 14.8 | 0.54238 | 2634.4 | 0.77% | 84.21 |
| S344 | 15.7 | 0.51039 | 3783.7 | 1.12% | 83.91 |
| S349 | 16.3 | 0.49118 | 3977.2 | 1.11% | 110.91 |
| S382 | 15.0 | 0.54135 | 2865.0 | 0.12% | 673.56 |
| S386 | 15.3 | 0.58875 | 4207.5 | 0.76% | 120.87 |
| S400 | 17.4 | 0.46516 | 3393.0 | 0.13% | 683.16 |
| S444 | 14.4 | 0.55619 | 2764.8 | 0.11% | 637.89 |
| S526 | 15.1 | 0.53000 | 2098.9 | 0.11% | 591.54 |
| S641 | 16.0 | 0.56250 | 5536.0 | 0.32% | 431.52 |
| S713 | 16.1 | 0.55919 | 5538.4 | 0.40% | 384.63 |
| S820 | 19.6 | 0.51196 | 13974.8 | 0.09% | 6086.97 |
| S832 | 18.5 | 0.54094 | 13320.0 | 0.09% | 6770.67 |
| S1423 | 15.4 | 0.58588 | 4527.6 | 2.05% | 47.85 |
| S1488 | 21.3 | 0.51687 | 28968.0 | 0.10% | 17396.07 |
| S1494 | 21.0 | 0.52381 | 28581.0 | 0.09% | 18599.91 |
| S2081 | 11.4 | 0.52727 | 638.4 | 11.40% | 1.59 |
В табл. 34.6 приведены результаты сокращения ДИ с помощью позиционной хеш-функции.
В табл. 34.7 представлены результаты сокращения ДИ с помощью одновходного сигнатурного анализатора.
В табл. 34.8 представлены результаты сокращения ДИ с помощью разновидности многовходного сигнатурного анализатора.
Эксперименты с тремя другими разновидностями рассматриваемых хеш-функций показали, что поиск хеш-функции с эффективностью сжатия от 0.58 до 0.67 наиболее вероятно завершается успехом за небольшое число шагов перебора, а наиболее привлекательным является использование в качестве хеш-функции одновходного сигнатурного анализатора.
| ДУ | 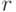 |
 |
Объем сокращенной ДИ, бит | Доля сокращенной ДИ от полной ДИ | Время подбора  , мс , мс |
|---|---|---|---|---|---|
| S298 | 13,3 | 0,60352 | 2367,4 | 0,69% | 231,24 |
| S344 | 14,2 | 0,56440 | 3422,2 | 1,02% | 265,98 |
| S349 | 14,2 | 0,56440 | 3464,8 | 0,96% | 313,08 |
| S382 | 13,6 | 0,58901 | 2597,6 | 0,11% | 1842,84 |
| S386 | 14,9 | 0,60536 | 4097,5 | 0,74% | 433,71 |
| S400 | 14,0 | 0,57260 | 2730,0 | 0,11% | 1968,96 |
| S444 | 14,1 | 0,56821 | 2707,2 | 0,10% | 1944,69 |
| S526 | 12,8 | 0,62711 | 1779,2 | 0,09% | 1440,39 |
| S641 | 15,4 | 0,58500 | 5328,4 | 0,31% | 1359,09 |
| S713 | 15,1 | 0,59732 | 5194,4 | 0,38% | 1097,70 |
| S820 | 17,4 | 0,57516 | 12406,2 | 0,08% | 15281,40 |
| S832 | 17,6 | 0,56897 | 12672,0 | 0,08% | 17568,15 |
| S1423 | 14,9 | 0,60482 | 4380,6 | 1,99% | 164,58 |
| S1488 | 19,1 | 0,57729 | 25976,0 | 0,09% | 40219,38 |
| S1494 | 19,1 | 0,57670 | 25995,1 | 0,08% | 40002,06 |
| S2081 | 9,7 | 0,62242 | 543,2 | 9,70% | 3,51 |
| ДУ | 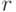 |
 |
Объем сокращенной ДИ, бит | Доля сокращенной ДИ от полной ДИ | Время подбора  , мс , мс |
|---|---|---|---|---|---|
| S298 | 13,4 | 0,59780 | 2385,2 | 0,69% | 746,4 |
| S344 | 14,1 | 0,57070 | 3398,1 | 1,01% | 826,26 |
| S349 | 14,1 | 0,56879 | 3440,4 | 0,96% | 910,53 |
| S382 | 13,4 | 0,59780 | 2559,4 | 0,11% | 5385,39 |
| S386 | 15,5 | 0,58223 | 4262,5 | 0,77% | 1403,01 |
| S400 | 13,8 | 0,58286 | 2691,0 | 0,10% | 5536,23 |
| S444 | 14,1 | 0,56879 | 2707,2 | 0,10% | 6073,62 |
| S526 | 12,4 | 0,64709 | 1723,6 | 0,09% | 4218,84 |
| S641 | 15,1 | 0,59723 | 5224,6 | 0,30% | 3673,95 |
| S713 | 15,7 | 0,57642 | 5400,8 | 0,39% | 3122,43 |
| S820 | 18,3 | 0,54949 | 13047,9 | 0,09% | 38325,81 |
| S832 | 17,6 | 0,56863 | 12672,0 | 0,08% | 37611,09 |
| S1423 | 17,0 | 0,53281 | 4998,0 | 2,27% | 568,5 |
| S1488 | 20,3 | 0,54297 | 27608,0 | 0,09% | 82035,57 |
| - S1494 | 19,9 | 0,55349 | 27083,9 | 0,08% | 80059,14 |
| S2081 | 11,9 | 0,50901 | 666,4 | 11,90% | 18,69 |
Результаты сокращения ДИ с помощью второй разновидности многовходного сигнатурного анализатора представлены в табл. 34.9.
Объем сокращенной с помощью хеш-функций ДИ в большинстве случаев составляет менее процента от исходного объема.
Стоит отметить, что дальнейшее увеличение длины диагностического теста , следствием которого является возрастание объема ДИ, по-видимому, может только улучшить показатели в предпоследнем столбце табл. 34.5- табл. 34.9, но не ухудшить их. Время поиска компактной свертки с помощью уже найденной хеш-функции для одной реакции на тест любого ДУ, упомянутого в табл. 33.1, составило менее 1 мс.
| ДУ |  |
 |
Объем сокращенной ДИ, бит | Доля сокращенной ДИ от полной ДИ | Время подбора 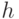 , мс , мс |
|---|---|---|---|---|---|
| S298 | 13,6 | 0,58901 | 2420,8 | 0,70% | 1314,27 |
| S344 | 14,1 | 0,56879 | 3398,1 | 1,01% | 1356,18 |
| S349 | 15,1 | 0,53000 | 3684,4 | 1,02% | 1579,26 |
| S382 | 13,5 | 0,59414 | 2578,5 | 0,11% | 8813,07 |
| S386 | 21,0 | 0,42857 | 5775,0 | 1,05% | 2957,4 |
| S400 | 14,0 | 0,57143 | 2730,0 | 0,11% | 9138,21 |
| S444 | 13,9 | 0,58039 | 2668,8 | 0,10% | 9929,79 |
| S526 | 13,0 | 0,61685 | 1807,0 | 0,10% | 7045,44 |
| S641 | 16,8 | 0,54000 | 5812,8 | 0,33% | 6170,34 |
| S713 | 17,0 | 0,54000 | 5848,0 | 0,43% | 5654,67 |
| S820 | 22,3 | 0,45380 | 15899,9 | 0,11% | 88089,66 |
| S832 | 18,3 | 0,54678 | 13176,0 | 0,08% | 61493,43 |
| S1423 | 95,0 | 0,09474 | 27930,0 | 12,67% | 4719,87 |
| S1488 | 28,0 | 0,39286 | 38080,0 | 0,13% | 208275 |
| S1494 | 21,0 | 0,52381 | 28581,0 | 0,09% | 126364,95 |
| S2081 | 10,9 | 0,57158 | 610,4 | 10,90% | 30,21 |
Сравнивая табл. 34.5-табл. 34.9 и табл. 33.2 можно утверждать, что сокращение ДИ с помощью хеш-функций оказалось эффективнее сокращения с помощью масок, полученных с помощью алгоритма 1, описанного в "Жадные алгоритмы поиска масок" . Так, объем информации, сокращенной с помощью найденных хеш-функций, оказался в среднем в пять раз меньше объема информации, сокращенного с помощью масок, а время, затраченное на получение маски, в среднем в шесть раз превышает время поиска хеш-функции.
Вместе с тем следует иметь в виду, что использование полученных с помощью хеш-функций словарей неисправностей при диагностировании имеет один недостаток. Так, если в технологическом процессе производства в тестовой аппаратуре для контроля ЦУ используется СА, играющий роль хеш-функции, то может возникнуть следующая проблема. Поскольку современные ЦУ имеют большое количество выходов, то оно, как правило, будет превышать число входов СА и потому ему для приема одной порции выходных значений ЦУ потребуется не один, а несколько временных тактов. Такая задержка повлечет увеличение времени вычисления свертки, т.е. замедлит технологический процесс. Понятно, что это может иметь негативные последствия для себестоимости производства ЦУ.
Ключевые термины:
Хеш-функция- функция преобразования (свертки) входного массива данных произвольной длины в выходную битовую последовательность фиксированной длины.
Полиномиальные и позиционные хеш-функции - две разновидности хеш-функций, характеризующиеся простотой и высокой скоростью вычисления их значений. Для их задания требуется только два параметра, один из которых есть разрядность результата.
Хеш-функции, порождаемые сигнатурным анализатором - функции, свойства которых определяются структурой используемого СА.
Краткие итоги:
В лекции описан метод сокращения ДИ, базирующийся на использовании свертки, получаемой с помощью пяти различных типов хеш-функций. Представленные экспериментальные данные подтверждают их высокую эффективность.
Вопросы и упражнения
- Опишите способы задания трех разновидностей хеш-функций.
- Какими параметрами задаются полиномиальные и позиционные хеш-функции?
- Как задаются хеш-функции, порождаемые сигнатурными анализаторами?
- Проанализируйте представленные в лекции экспериментальные данные, касающиеся применения различных типов хеш-функций, и сравните их эффективность и предпочтительные области использования.

