Оценка эффективности генетических алгоритмов поиска масок

В предыдущей лекции были описаны простые генетические алгоритмы для поиска масок. Интерес представляют вопросы, касающиеся оценки времени поиска масок с использованием этих алгоритмов.Кроме того, если речь идет о приближенном решении, то интересна также оценка удаленности такого решения от оптимального и скорости сходимости процесса поиска к оптимальному решению.

Вначале приведем утверждение об оценке вычислительной сложности описанных в предыдущей лекции ПГА.

Введем следующие обозначения. Пусть - число этапов эволюции, реализуемых ГА, - число особей в популяции, 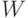- объем памяти (в битах) для хранения одной особи.

Теорема. Пусть для ЦУ с множеством неисправностей получен СПР. Тогда оценка алгоритмической сложности одного запуска генетического алгоритма со структурой хромосомы (29.1) или (29.6) и с использованием любой из фитнес-функций (29.3)-(29.5), (29.7)-(29.10) равна , а объем памяти, необходимой для работы генетического алгоритма, равен .

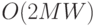Доказательство. На каждом этапе эволюции должно быть вычислено значение фитнес-функции каждой особи в популяции, после чего особи должны быть упорядочены по значениям их приспособленности.

Исходя из вида формул (29.3)-(29.5), (29.7)-(29.10), оценка вычислительной сложности для функций приспособленности сводится к оценке вычислительной сложности величин и 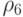. Согласно [1] вычислительная сложность величины оценивается величиной

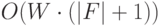( 30.1)

Для вычисления значения 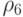необходимо также произвести

( 30.2)

сравнений. Сортировка элементов популяции производится за время

( 30.3)

Принимая во внимание тот факт, что в процессе эволюции должно быть найдено поколений, а также с учетом (30.1) -(30.3) , получим оценку вычислительной сложности, приведенную в формулировке теоремы.

На каждом этапе эволюции требуется хранение двух поколений: родительской популяции и популяции дочерних особей. Отсюда емкостная сложность генетического алгоритма для задач минимизации и оптимизации диагностической информации оценивается величиной .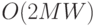

Заметим, что один из возможных способов ускорения времени работы ПГА состоит в их распараллеливании.

Генетические алгоритмы предоставляют множество возможностей для реализации на архитектуре, допускающей параллельные процессы.

Самый простой способ распараллелить ГА - распараллелить процесс выполнения его операторов и вычисление значения фитнес-функции. В случае параллельных операторов алгоритм будет работать следующим образом. Базовый поток порождает рабочие потоки, которые могут обмениваться сообщениями с базовым с помощью некоторого интерфейса. Когда вычисления в базовом потоке доходят до параллельного оператора, формируются задания рабочим потокам. Популяция делится на равные части (по количеству рабочих потоков) и каждая часть посылается соответствующему рабочему потоку. Базовый поток продолжает свою работу после получения результатов от всех рабочих потоков. Если в процессе ожидания результатов делается вывод о некорректном завершении какого-либо рабочего потока, задание посылается повторно другому рабочему потоку, свободному в данный момент.

Важно заметить, что при такой организации ГА ему безразлично, как и в какой среде передаются сообщения, поэтому этот способ подходит для вычислительных систем любой организации: однопроцессорных ЭВМ, многопроцессорных ЭВМ или кластеров любой структуры. Эффективность такого распараллеливания зависит прежде всего от скорости передачи сообщений между потоками. Если рассматривать многопроцессорную ЭВМ с общей памятью, где скороcть передачи данных между потоками максимальна, то распараллеливание любых операторов эффективно практически во всех случаях, т. к. генотипы, хранящиеся в общей памяти, не копируются для каждого рабочего потока, а используются совместно.

Если же рассматривать кластер, где оперативная память у потоков разделена, а передача сообщений производится через локальную сеть, то необходимо произвести детальный анализ последствий распараллеливания того или иного оператора с точки зрения потерь производительности алгоритма при передаче сообщений между потоками. В целом, оператор целесообразно распараллеливать, если вычисление результата для каждого генотипа занимает гораздо большее время, чем передача генотипа в сообщении потоку и прием ответа.

Качественные оценки вычислительной сложности ПГА, полученные в сформулированной выше теореме, несомненно представляют интерес, но значительно больший интерес представляют экспериментальные данные, полученные для различных реальных ЦУ. Ниже будет представлена статистика, полученная в результате проведения численных экспериментов как на исходных данных, генерируемых случайным образом, так и на реальной ДИ для некоторых реальных ДУ.

Результаты экспериментов, демонстрируемые ниже в табл. 30.1-30.7, получены на PC Pentium III, 1024 MHz, 256 MB RAM и частично отражены в [5].

Данные об эффективности применения представленного выше простого ГА для минимизации информации (1-я из задач, сформулированных в лекции 4) при поиске маски приведены в табл. 30.1 (эти результаты получены на случайных исходных данных).

Таблица 30.1.

		Объем ДИ, бит	Объем маски, бит	Время работы ПГА	Доля сокращенной информации по отношению к полной
127	40	5 080	9	48 сек	22.5%
511	256	130 816	12	6 мин	4.68%
1023	512	523 776	18	12 мин	3.51%
2047	1024	2 096 128	19	2 час 7 мин	1.85%
4095	1024	4 192 256	24	15 час	2.34%

Эти данные были получены с использованием оператора отбора линейным ранжированием и оператора булева скрещивания. Применение других типов операторов, перечисленных нами ранее, как показали численные эксперименты, требуют в среднем больших временных затрат на поиск оптимальной маски и при этом дают меньшие размеры сокращения информации.

В процессе проведения расчетов было эмпирически установлено, что численность популяции достаточно ограничить 50 особями, а длину жизненного цикла - 50 поколениями.

В табл. 30.2 для сравнения приведены результаты решения той же задачи поиска оптимальной маски методом полного перебора.

Таблица 30.2.

		Объем ДИ, бит	Объем маски, бит	Время поиска маски	Доля сокращенной информации по отношению к полной
70	20	1 400	9	15 мин	45%
127	21	2 667	10	46 мин	47%
127	22	2 794	10	1 час 32 мин	45%
127	23	2 921	10	4 час 25 мин	43%
127	30	3 810	10	более суток	33%

Как видно из этой таблицы, даже для довольно скромных размеров исходной информации (общий объем не превышал 3810 бит) поиск решения требует очень больших временных затрат. Отсюда можно сделать вывод, что для реальных задач классификации объектов с большим числом признаков (более 100) применения перебора неприемлемо.

Перейдем теперь к оценке эффективности применения разработанного простого ГА для оптимизации информации при поиске маски на случайных данных. Соответствующие результаты приведены в табл. 30.3.

Таблица 30.3.

		Объем ДИ, бит	Заданный объем маски, бит		Время работы ПГА	Доля сокращенной информации по отношению к полной
127	40	5 080	7	1.01	7 сек	17.5%
511	256	130 816	9	1.07	42 сек	3.51%
1023	512	523 776	10	1.12	1 мин	1.95%
2047	1024	2 096 128	11	1.21	35 мин	1.07%
4095	1024	4 192 256	12	1.27	1 час 22 мин	1.17%

Напомним, что данные, приведенные в табл. 30.3, были получены с применением специальных операторов булева кроссовера и мутации. При такой организации выполнения скрещивания и мутации в каждом новом поколении присутствуют особи с одним и тем же числом единиц в представляющих их хромосомах, т. е. особи-маски одного и того же объема. В связи с этим для решения задачи оптимизации информации вместо фитнес-функции (29.4) выгодно использовать фитнес-функцию (29.5), для которой ПГА должен найти минимум. Такое упрощение приводит к сокращению времени работы алгоритма.

Попытки находить решение 2-ой задачи методом полного перебора показали, что здесь ситуация полностью аналогична той, что имела место для 1-ой задачи. Для реальных задач поиска маски при длине полной реакции ДУ более 100 бит метод простого перебора практически не применим.

Приведем данные для сокращения ДИ конкретных реальных устройств. В следующей серии экспериментов была использована ДИ, полученная для ЦУ из каталога ISCAS'89 [2] при моделировании одиночных неисправностей с помощью вероятностных последовательностей в качестве диагностического теста. Каждый вероятностный тест был составлен из 100 входных наборов. В множество технических состояний для ДУ было включено исправное состояние, а также по одному представителю от каждого множества неотличимых друг от друга с помощью этого теста неисправностей.

Табл. 30.4 представляет динамику нахождения решения задачи минимизации ДИ для ЦУ из набора схем каталога ISCAS'89.

Данные, приведенные в этой таблице, так же как и в табл. 30.1, получены с применением выбора линейным ранжированием, оператора однородного кроссовера и фитнес-функции (4.1).

Табл. 30.5 показывает динамику нахождения решения задачи 2 для некоторых схем из набора ISCAS'89.

Таблица 30.4.

Схема			Объем полной ДИ	Результат после 40 поколений		Результат после 60 поколений		Результат после 80 поколений		Доля сокращенной информации по отношению к полной
				Объем маски		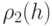Объем маски		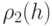Объем маски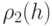
S298	600	92	55 200	100	1.022	86	1.000	72	1.000	12.00%
S349	1100	184	202 400	183	1.033	175	1.000	156	1.000	14.18%
S382	600	32	19 200	39	1.062	37	1.062	38	1.000	6.33%
S386	700	137	95 200	145	1.015	132	1.000	117	1.000	16.71%
S400	600	33	19 800	44	1.000	41	1.000	37	1.000	6.17%
S510	700	447	312 900	320	1.000	255	1.000	206	1.000	29.43%
S526	600	23	13 800	31	1.000	30	1.000	29	1.000	4.83%
S8381	100	86	8 600	23	1.000	18	1.000	18	1.000	18.00%
S1494	1900	322	611 800	345	1.118	370	1.031	373	1.000	19.63%
S4201	100	61	6 100	20	1.000	19	1.000	19	1.000	19.00%

Таблица 30.5.

Схема			Объем полной ДИ	Результат после 40 поколений		Результат после 60 поколений		Результат после 80 поколений		Доля сокращенной информации по отношению к полной
				Объем маски		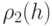Объем маски		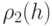Объем маски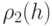
S382	600	32	19 200	20	1.063	20	1.000	20	1.000	3.33%
S386	700	136	95 200	55	1.059	55	1.044	55	1.000	7.86%
S400	600	33	19 800	20	1.121	20	1.060	20	1.000	3.33%
S510	700	447	312 900	70	1.027	70	1.000	70	1.000	10.00%

Так же как и в табл. 30.3 эти данные получены с применением специальных операторов кроссовера и мутации и фитнес-функции (29.4).

Стоит отметить, что, как показывает опыт, значительное увеличение длины вероятностного диагностического теста приводит к довольно малому росту числа обнаруженных с его помощью неисправностей. По этой причине увеличение длины теста, следствием которого является возрастание объема ДИ, по-видимому, может только улучшить показатели в последнем столбце таблиц 30.4 и 30.5, но не ухудшить их.

Эксперименты по нахождению индивидуальных масок проводились для ДИ полученной для ДУ из каталога ISCAS'89 при моделировании одиночных неисправностей с помощью тестовых последовательностей HITEC[3]. Так же как и в предыдущем случае в множество технических состояний было включено по одному представителю от каждого класса эквивалентности на множестве всевозможных технических состояний.