|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Представление диагностической информации
Процесс диагностирования ЦУ требует использования так называемой диагностической информации (ДИ). Для реальных современных ЦУ эта информация имеет очень большой обьем, что порождает значительные трудности при обнаружении и локализации неисправностей.
Решению проблемы уменьшения объема (сокращения) ДИ посвящено много работ российских и зарубежных ученых, в которых были предложены различные подходы и методы. Следует отметить, что "проклятие размерности", как это происходит и в других предметных областях, не удается "ликвидировать" неким универсальным способом. По этой причине были сделаны попытки создания приемлемых по эффективности методов сокращения (компрессии) ДИ с использованием различных средств, включая, например, специальные методы проектирования ЦУ, особую организацию самой ДИ, специализированную аппаратуру и т.п. Вместе с тем каждый из перечисленных подходов имеет свои достоинства и недостатки и ограниченную сферу применения. Несмотря на большое число работ в указанном направлении, в целом прблема сокращения ДИ остается открытой до сегодняшнего дня.
Под термином "диагностическая информация" понимают совокупность данных, наличие которых необходимо для проведения процесса диагностирования. Содержание диагностической информации зависит от применяемой технологии диагностирования. Однако в любом случае ДИ должна содержать в себе данные о каждом тестовом воздействии, информацию о составе контрольных точек ЦУ, с которых "снимаются" его реакции на тестовые воздействи, ожидаемые результаты тестовых воздействий, а также данные о последовательности подачи тестовых воздействий в процессе диагностирования.
Ожидаемые результаты тестовых воздействий могут быть оформлены заданием явной математической модели объекта диагностирования.
Такую модель часто представляют в табличной форме с помощью так называемой таблицы функций неисправностей (ТФН). Эта таблица является прямоугольной. Каждой ее строке ставится в соответствие техническое состояние объекта диагностирования из множества  , а столбцам - тестовые наборы
, а столбцам - тестовые наборы 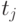 из множества
из множества  , с использованием которого диагностируется ЦУ. В клетке таблицы, находящейся на пересечении
, с использованием которого диагностируется ЦУ. В клетке таблицы, находящейся на пересечении  -ой строки и
-ой строки и  -го столбца, помещается результат (реакция)
-го столбца, помещается результат (реакция)  объекта диагностирования, находящегося в техническом состоянии
объекта диагностирования, находящегося в техническом состоянии 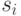
Если множество тестов  обладает свойством обнаружения любой неисправности из множества
обладает свойством обнаружения любой неисправности из множества  всех рассматриваемых допустимых неисправностей, т. е. для любой неисправности
всех рассматриваемых допустимых неисправностей, т. е. для любой неисправности  найдется хотя бы один тестовый набор
найдется хотя бы один тестовый набор 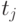 такой , что
такой , что  , то все строки ТФН отличны от первой строки (здесь
, то все строки ТФН отличны от первой строки (здесь  - реакция исправного ЦУ на тест
- реакция исправного ЦУ на тест 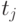 ). Если же множество
). Если же множество  обладает также свойством различения всех неисправностей из множества
обладает также свойством различения всех неисправностей из множества  , т. е. для каждой пары неисправностей
, т. е. для каждой пары неисправностей  ,
, , найдется хотя бы один тестовый набор
, найдется хотя бы один тестовый набор 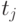 такой, что
такой, что  , то все строки таблицы, представляющие неисправные состояния, попарно различны.
, то все строки таблицы, представляющие неисправные состояния, попарно различны.
В качестве примера проиллюстрируем построение таблицы функций неисправностей устройства, изображенного на рис. 27.1(комбинационная схема С17 из каталога ISCAS-85).
Пусть множество неисправностей ограничено восемью неисправностями, представленными в табл. 27.1.

|
Константа единица на входе 3 |
|---|---|
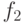
|
Константа единица на первом входе блока 7 |

|
Константа ноль на выходе блока 7 |
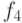
|
Константа единица на выходе блока 8 |
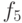
|
Константа единица на втором входе блока 10 |

|
Константа ноль на выходе блока 10 |

|
Константа ноль на выходе блока 11 |

|
Константа единица на входе 2 |
Через 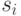 обозначим техническое состояние устройства, содержащее неисправность
обозначим техническое состояние устройства, содержащее неисправность 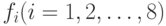 .
.
Каждый тестовый набор 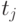 будем далее именовать также элементарной проверкой и обозначать через
будем далее именовать также элементарной проверкой и обозначать через  .
.
В табл. 27.2 представлены все возможные тестовые воздействия, используемые для проверки устройства С17. Каждая элементарная провека  представлена пятизначным двоичным кодом , в котором значения разрядов, перенумерованных слева направо, равны значениям сигналов, подаваемых на входы 1- 5 устройства.
представлена пятизначным двоичным кодом , в котором значения разрядов, перенумерованных слева направо, равны значениям сигналов, подаваемых на входы 1- 5 устройства.

|
00000 |

|
00010 |

|
00001 | 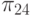
|
00011 |
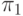
|
10000 |
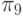
|
10010 |
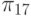
|
10001 |

|
10011 |

|
01000 |

|
01010 |

|
01001 |

|
01011 |
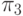
|
11000 | 
|
11010 |

|
11001 |

|
11011 |
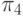
|
00100 |

|
00110 |

|
00101 |

|
00111 |
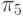
|
10100 |

|
10110 | 
|
10101 |

|
10111 |

|
01100 |

|
01110 |

|
01101 |

|
01111 |
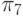
|
11100 |

|
11110 |
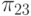
|
11101 | 
|
11111 |
Результат построения ТФН для устройства C17 представлен в табл. 27.3. Содержимое каждой клетки этой таблицы представляет собой двузначный двоичный код, первый разряд которого соответствует значению на выходе 12, а второй - значению на выходе 13.
Из анализа построенной ТФН можно сделать вывод, что множество T элементарных проверок обладает свойством обнаружения любой неисправности из множества  : проверка
: проверка 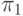 отличает
отличает  от состояний
от состояний  и
и  , проверка
, проверка  - от состояний
- от состояний  ,
, 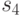 ,
,  ,
,  и
и  , а
, а  отличает
отличает  от
от  . Множество
. Множество  обладает также свойством различения всех неисправностей из множества
обладает также свойством различения всех неисправностей из множества  . Действительно, проверка
. Действительно, проверка 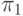 различает состояния
различает состояния  и
и  между собой и отличает их от остальных состояний. Таким же образом пр
оверка
между собой и отличает их от остальных состояний. Таким же образом пр
оверка  различает между собой и отличает от других технические состояния
различает между собой и отличает от других технические состояния  ,
,  ,
,  , а оставшиеся состояния
, а оставшиеся состояния 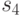 и
и  различает между собой проверка
различает между собой проверка  .
.
Таблица неисправностей, как универсальная математическая модель объекта диагностирования, очень наглядна и удобна при обсуждении и классификации принципов, а также основных процедур построения и реализации алгоритмов диагностирования, даже если эти принципы и процедуры первоначально формулируются на языках, отличных от языка таблиц функций неисправностей.
Однако непосредственное использование таблицы функций неисправностей как формы представления информации при построении и реализации алгоритмов диагностирования и физических моделей объектов диагностирования часто невозможно из-за большой размерности таблицы.
Вместо полных ТФН в процессах диагностирования практическое применение получили так называемые  -таблицы функций неисправностей.
-таблицы функций неисправностей.

|

|

|

|

|
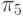
|

|
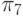
|

|
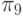
|

|

|

|

|

|

|
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

|
00 | 00 | 11 | 11 | 00 | 10 | 11 | 11 | 00 | 00 | 11 | 11 | 00 | 10 | 00 | 10 |

|
00 | 10 | 11 | 11 | 00 | 10 | 11 | 11 | 00 | 10 | 00 | 10 | 00 | 10 | 00 | 10 |

|
00 | 00 | 11 | 11 | 00 | 10 | 11 | 11 | 00 | 00 | 00 | 00 | 00 | 10 | 00 | 10 |

|
00 | 00 | 00 | 00 | 00 | 00 | 00 | 10 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 10 |

|
00 | 00 | 00 | 00 | 00 | 10 | 00 | 10 | 00 | 00 | 00 | 00 | 00 | 10 | 00 | 10 |

|
00 | 00 | 01 | 01 | 00 | 10 | 01 | 11 | 00 | 00 | 01 | 01 | 00 | 10 | 00 | 10 |

|
00 | 00 | 01 | 01 | 00 | 00 | 01 | 01 | 00 | 00 | 01 | 01 | 00 | 00 | 00 | 00 |

|
00 | 00 | 10 | 10 | 00 | 10 | 10 | 10 | 00 | 00 | 10 | 10 | 00 | 10 | 00 | 10 |

|
11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 00 | 10 | 00 |

|
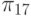
|

|

|

|

|

|
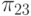
|
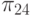
|

|

|

|

|

|

|

|
|

|
01 | 01 | 11 | 11 | 01 | 11 | 11 | 11 | 11 | 01 | 11 | 11 | 00 | 10 | 00 | 10 |

|
01 | 11 | 11 | 11 | 01 | 11 | 11 | 11 | 00 | 10 | 00 | 10 | 00 | 10 | 00 | 10 |

|
01 | 01 | 11 | 11 | 01 | 11 | 11 | 11 | 00 | 00 | 00 | 00 | 00 | 10 | 00 | 10 |

|
00 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 00 | 10 | 00 | 10 |

|
01 | 01 | 01 | 01 | 01 | 11 | 01 | 11 | 01 | 01 | 01 | 01 | 00 | 10 | 00 | 10 |

|
01 | 01 | 01 | 01 | 01 | 11 | 01 | 11 | 01 | 01 | 01 | 01 | 00 | 10 | 00 | 10 |

|
01 | 01 | 01 | 01 | 01 | 01 | 01 | 01 | 01 | 01 | 01 | 01 | 00 | 00 | 00 | 00 |

|
00 | 00 | 10 | 10 | 00 | 10 | 10 | 10 | 10 | 00 | 10 | 10 | 00 | 10 | 00 | 10 |

|
10 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 00 | 10 | 00 | 10 |
Как видно из приведенного примера, полная ТФН может содержать большой объем избыточной информации, который можно сократить. Определение совокупности  элементарных проверок, входящих в алгоритм диагностирования, соответствует выделению определенной совокупности столбцов таблицы функций неисправностей. Для алгоритмов проверки исправности, работоспособности или правильности функционирования устройства эта совокупность столбцов такова, что строка образуемой ими подтаблицы ТФН, соответствующая техническому состоянию
элементарных проверок, входящих в алгоритм диагностирования, соответствует выделению определенной совокупности столбцов таблицы функций неисправностей. Для алгоритмов проверки исправности, работоспособности или правильности функционирования устройства эта совокупность столбцов такова, что строка образуемой ими подтаблицы ТФН, соответствующая техническому состоянию  , отличается от любой другой ее строки. Аналогично, для алгоритмов поиска неисправностей все строки такой подтаблицы ТФН попарно различны.
, отличается от любой другой ее строки. Аналогично, для алгоритмов поиска неисправностей все строки такой подтаблицы ТФН попарно различны.
Подтаблицу, образованную совокупностью столбцов ТФН, соответствующих элементарным проверкам из  , будем называть
, будем называть  -таблицей функций неисправностей (
-таблицей функций неисправностей ( -ТФН).
-ТФН).
Возможное содержимое  -ТФН для алгоритма поиска неисправностей устройства C17 из последнего примера приведено в табл. 27.4.
-ТФН для алгоритма поиска неисправностей устройства C17 из последнего примера приведено в табл. 27.4.

