|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Эволюционные методы генерации тестов
25.5 Реализация генетического алгоритма генерации тестов
Общий подход к тестированию заключается в следующем. Процесс генерации тестов содержит три фазы. Цель первой фазы - активизация неисправности, т.е. распространение рассогласования сигнала на псевдовыходы. На начальном этапе, когда необходимо как можно быстрее активизировать и проверить большее число неисправностей, используется псевдослучайный метод генерации тестовых последовательностей. На втором этапе для повышения эффективности процесса активизации неисправностей используется генетический алгоритм. После того, как в первой фазе активизирована какая-либо неисправность, необходимо улучшить полученную активизирующую последовательность так, чтобы она стала проверяющей. Для этого во второй фазе также используется генетический алгоритм. Фаза 2 является ядром всего алгоритма. После выполнения второй фазы в случае успешного результата - построения тестовой последовательности, необходимо произвести моделирование с неисправностями на данной последовательности (фаза три), чтобы обнаружить все неисправности, которые она проверяет. Укрупненный алгоритм в виде псевдокода представлен на рис. 25.10. Здесь переменная режим показывает, каким способом ведётся активизация неисправности: значение 0 соответствует псевдослучайному метод, 1 - генетическому алгоритму. Переменная метод показывает цель, для которой используется генетический алгоритм. При этом значение 0 соответствует активизации неисправности, а 1 - построению теста для активизированной неисправности.
В данном алгоритме каждая особь представляет тестовую последовательность, длина которой заранее не известна и не ограничена (рис. 25.6 а.). Она состоит из векторов, каждый бит которых соответствует входу схемы. В свою очередь популяция состоит из заранее заданного числа особей (рис. 25.6 б).). Одной из главных задач при построении генетического алгоритма является задание оценочной функции, которая должна показывать насколько близко данная особь приблизилась к решению задачи.
Качество тестовой последовательности оценивается как мера отличия значений сигналов в исправной и неисправной схемах. Эта оценка основывается на предположении о том, что, чем выше активность в неисправной схеме производит неисправность, тем легче она может быть обнаружена. Оценочная функция последовательности для фиксированной неисправности вычисляется из оценочных функций всех её векторов по формуле:
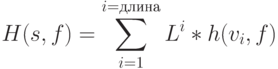
где  - анализируемая последовательность;
- анализируемая последовательность;  - вектор из рассматриваемой последовательности,
- вектор из рассматриваемой последовательности,  - позиция вектора в последовательности,
- позиция вектора в последовательности,  - заданная неисправность,
- заданная неисправность,  - предварительно заданная константа в диапазоне
- предварительно заданная константа в диапазоне 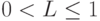 , благодаря которой предпочтение отдаётся более коротким последовательностям. Здесь оценочная функция одного вектора из последовательности имеет вид:
, благодаря которой предпочтение отдаётся более коротким последовательностям. Здесь оценочная функция одного вектора из последовательности имеет вид:
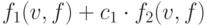
где  константа нормирования, равная отношению числа вентилей схемы к числу триггеров;
константа нормирования, равная отношению числа вентилей схемы к числу триггеров;  и
и  эвристические функции, определяющие:
эвристические функции, определяющие:
-
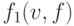 взвешенное число вентилей с различными значениями сигналов в исправной и неисправной схемах;
взвешенное число вентилей с различными значениями сигналов в исправной и неисправной схемах;
-
 взвешенное число триггеров с различными значениями сигналов в исправной и неисправной схемах.
взвешенное число триггеров с различными значениями сигналов в исправной и неисправной схемах.
В качестве веса выбирается мера наблюдаемости элемента схемы, вычисляемая на этапе предварительной обработки схемы. В алгоритме используется виды скрещивания, описанные выше, выбор между которыми производится случайно При горизонтальном скрещивании случайным образом в последовательностях-родителях выбираются точки разреза 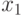 и
и 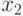 .
Первый потомок получается соединением векторов первого родителя от начала последовательности до точки деления
.
Первый потомок получается соединением векторов первого родителя от начала последовательности до точки деления 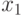 и второго родителя от точки деления
и второго родителя от точки деления 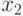 до конца последовательности. Второй потомок получается аналогично при перемене мест первого и второго родителя.
Вертикальное скрещивание производится не по наборам теста, а по входным сигналам схемы. Для получения потомка необходимо взять первый столбец из таблицы - теста первого родителя и случайным образом определить, будет ли он столбцом первого или второго потомка. Легко заметить, что при горизонтальном пересечении длина последовательностей-особей может, как уменьшаться, так и увеличиваться, тогда, как при вертикальном скрещивании длина обоих потомков станет равной длине большего из родителей. При этом все "пустоты", получаемые из-за разности длин заполняются случайными битами.
до конца последовательности. Второй потомок получается аналогично при перемене мест первого и второго родителя.
Вертикальное скрещивание производится не по наборам теста, а по входным сигналам схемы. Для получения потомка необходимо взять первый столбец из таблицы - теста первого родителя и случайным образом определить, будет ли он столбцом первого или второго потомка. Легко заметить, что при горизонтальном пересечении длина последовательностей-особей может, как уменьшаться, так и увеличиваться, тогда, как при вертикальном скрещивании длина обоих потомков станет равной длине большего из родителей. При этом все "пустоты", получаемые из-за разности длин заполняются случайными битами.
Механизм мутации обеспечивает появление новых генов в особях. Он применяется с заранее заданной вероятностью  к результатам операции скрещивания. В алгоритме применяется три приведенные выше вида мутации, выбор между которыми происходит случайно.
к результатам операции скрещивания. В алгоритме применяется три приведенные выше вида мутации, выбор между которыми происходит случайно.
Остановимся теперь подробнее на фазах алгоритма. Целью 1-й фазы является определение неисправности, которая может быть активизирована. При этом значения сигналов в присутствии неисправности, отличные от значений исправной схемы, могут быть распространены на внешние псевдовыходы. Для этого производится моделирование неисправностей для нескольких последовательностей. После этого выбирается лучшая из последовательностей. Если она активизировала какую-либо неисправность, то эта неисправность выбирается в качестве целевой неисправности и происходит переход во вторую фазу алгоритма. В начале работы алгоритма в качестве лучшей последовательности выбирается та, которая обнаружила больше неисправностей. При этом, за несколько проходов моделирования строится тест для большинства легко тестируемых неисправностей. На более поздних этапах в качестве лучшей последовательности выбирается та, которая активизировала наибольшее число неисправностей или произвела наибольшую активность сигналов (изменений) в схеме. Для этой цели также используется генетический алгоритм. При этом оценочные функции будут аналогичны тем, которые используются в фазе 2, поскольку несут ту же смысловую нагрузку. Метод активизации неисправностей в алгоритме показывает переменная режим. Длина последовательностей в фазе 1 в начальный момент считается заданной, а далее полагается равной длине проверяющей последовательности, сгенерированной в фазе 2 алгоритма.
Целью 2-й фазы является улучшение активизирующей последовательность таким образом, чтобы она стала проверяющей для целевой неисправности. Эта фаза является ключевой в алгоритме. Её псевдокод приведён на рис. 25.11. Здесь  - текущая популяция, которая в начальный момент инициализируется особями из фазы 1 алгоритма,
- текущая популяция, которая в начальный момент инициализируется особями из фазы 1 алгоритма,  - следующее поколение,
- следующее поколение,  - две новых последовательности, получаемых в результате операции скрещивания. Вычисление новых популяций производится ограниченное число раз (MAX_ПОКОЛЕНИЙ). Если за это время тестовая последовательность не найдена, то целевая неисправность отмечается, как непроверяемая и больше не может быть вновь выбрана в качестве цели генетического алгоритма.
- две новых последовательности, получаемых в результате операции скрещивания. Вычисление новых популяций производится ограниченное число раз (MAX_ПОКОЛЕНИЙ). Если за это время тестовая последовательность не найдена, то целевая неисправность отмечается, как непроверяемая и больше не может быть вновь выбрана в качестве цели генетического алгоритма.
Поиск_проверяющей_последовательности(неисправность-цель)
\{
for( i=0 ; i<MAX_ПОКОЛЕНИЙ ; i++)
\{
for( каждой особи s в популяции P )
вычислить_оценку(s, f );
newP=*;
for( k=0 ; k<ЧИСЛО_НОВЫХ_ОСОБЕЙ ; k++ )
\{
выбрать_две_последовательности_в_P();
применить_операцию_скрещивания();//генерируются две особи
применить_операцию_мутации_к_s_c_вероятностью_P_{m}();
newP=newP*s;
\}
P=(лучшие MAX_ОСОБЕЙ из newP и P )
for( каждой особи s в популяции P )
if( s обнаруживает f )
return s;
\}
return( НЕТ_ПОСЛЕДОВАТЕЛЬНОСТИ )
\}
Если в процессе второй фазы, генетический алгоритм породил тестовую последовательность, то происходит переход к фазе 3. Здесь производится моделирование всех необнаруженных (на текущем этапе) неисправностей на данной тестовой последовательности. По данным моделирования (вновь) проверяемые неисправности вычёркиваются из списка неисправностей и далее не рассматриваются.
В качестве вспомогательного инструмента используются программы моделирования с неисправностями. В первой программе моделирования используется параллельное по неисправностям моделирование (описанное в "Последовательное и параллельное моделирование неисправностей" ).
Вторая программа моделирования неисправностей реализует алгоритм "параллельного моделирования по тестовым наборам" ( "Последовательное и параллельное моделирование неисправностей" ) и написана специально для работы с генетическим алгоритмом. При этом во всех битах машинного слова моделируется одна и та же неисправность (в алгоритме - целевая неисправность), но на каждый разряд подаётся своя тестовая последовательность-особь. Таким образом, реализуется параллельное моделирование по особям популяции. При этом после моделирования очередного тестового вектора происходит вычисление его оценочной функции. После моделирования всех тестовых последовательностей вычисляется оценочная функция всей последовательности. Вычисление оценочных функций особей является самым трудоёмким этапом в алгоритме. Поэтому применение данного подхода существенно повышает скорость вычисления оценочных функций особей в популяции и скорость работы алгоритма в целом. Недостатком такого подхода является ограниченное число особей в популяции: не более 32-х, что обусловлено разрядностью инструментальной ЭВМ. Однако это ограничение несущественно, поскольку число особей в популяции (МАХ_ОСОБЕЙ) обычно выбирается гораздо меньше: 8, 16 или 24 особи.
Ключевые термины:
Генетический алгоритм - алгоритм поиска решения, основанный на принципах, сходных с принципами естественного отбора..
Особь - потенциальное решение рассматриваемой проблемы.
Популяции - множество особей - потенциальных решений.
Кроссинговер - генетические оператор, при выполнении которого с заданной вероятностью особи обмениваются генами - частями потенциальных решений.
Мутация - генетический оператор, где с малой вероятностью случайно изменяется значение гена.
Фитнесс-функция - характеризует качество потенциального решения проблемы.
Краткие итоги
В лекции рассмотрено применение генетического алгоритма к решению задачи построения проверяющих тестов.
В "Эволюционные методы генерации тестов" изложены основные понятия простого генетического алгоритма, определены основные генетические операторы репродукции, кроссинговера и мутации.
В "Выполнимость булевых функций и бинарные диаграммы в построении тестов" описано применение генетического алгоритма для построения пролверяющих тестов комбинационных цифровых схем. В этом случае в качестве особи выступает отдельный входной набор и на каждом шаге ГА выбирает лучший набор, который включается в тест
"Эволюционные методы генерации тестов" описывает применение ГА для построения тестов последовательностной схемы. Здесь в качестве особе выступает тестовая последовательность и генетические операторы кроссинговера и мутации определены над двоичными таблицами.
В "Эволюционные методы генерации тестов" приведены основные виды фитнесс-функций, которые используются для оценки качества потенциальных решений при построении проверяющих тестов.
"Эволюционные методы генерации тестов" посвящен вопросам реализации генетического алгоритма построения проверяющих тестов, изложены основные этапы генерации тестов.
Вопросы и упражнения
- Какие генетические операторы используются в ГА?
- Какую роль в ГА играет оператор репродукции (ОР)?
- Опишите 1-точечный оператор кроссинговера (ОК) и приведите пример его работы.
- Придумайте другую реализацию ОК.
- Какую роль играет оператор мутации (ОМ) ?
- Опишите ОМ и приведите пример его работы.
- Придумайте другую реализацию ОМ.
- Какие основные параметры ГА ?
- Как можно использовать ГА при построении тестов для комбинационных схем?
- Что выступает в качестве особи при использовании ГА для комбинационных схем?
- Какие при этом используются генетичесакие операторы?
- Как в этом случае определяется фитнесс-функции?
- Что выступает в качестве особи при использовании ГА для построения тестов для последовательностных схем?
- Опишите гентические операторы кроссинговера, которые можно использовать для последовательностных схем.
- Опишите возможные операторы мутации.
- Какие виды фитнесс-функций используются при построении тестов для последовавтельностных схем?
- От каких параметров может зависеть фитнесс-функция при генерации тестов?
- Опишите основные этапы возможной реализации генетическиого алгоритма построения тестов.


