Эволюционные методы генерации тестов

25.4 Проблемно-ориентированные фитнесс-функции для генерации тестов

Поскольку целью генерации тестов является построение последовательности, на которой максимально отличаются значения сигналов в исправной и неисправной схемах, то качество тестовой последовательности (fitness-функция) оценивается как мера отличия значений сигналов в исправной и неисправной схемах. В программных системах генерации тестов используются различные fitness-функции, зависящие от следующих основных параметров, которые приведены в табл. 25.6.

Таблица 25.6.

	Число узлов в схеме
	Число узлов, имеющих различные значения сигналов в исправной и неисправной схемах
	Число триггеров в схеме
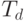
	Число триггеров, изменивших состояние
	Число событий в исправной и неисправной схеме
	Длина тестовой последовательности
	Число неисправностей в схеме
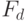
	Число проверенных неисправностей
	Число неисправностей, активизированных до триггеров
	Обнаруживаемость неисправности
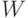
	Мощность последовательности
	Наблюдаемость триггеров
	Число событий в неисправной схеме
	Число трудно устанавливаемых триггеров

Помимо них характеристики алгоритмов генерации тестов существенно зависят от стандартных параметров ГА таких как мощность популяции, вероятности репродукции, кроссинговера и мутации, числа поколений и т.д.

В системе CRIS [25.6] используется техника иерархического моделирования, сокращающая затраты памяти и позволяющая обрабатывать схемы большой размерности. Здесь применяется традиционный ГА, в котором популяции эволюционируют посредством операторов мутации и кроссинговера. В качестве особи берется последовательность входных наборов. Система CRIS основывается прежде всего на непрерывной мутации данной входной тестовой последовательности и анализе мутировавших наборов путем моделирования, в основном, исправных схем с целью определения тестового множества. Данная система показала хорошие результаты при построении тестов с высоким уровнем покрытия неисправностей в комбинационных и последовательностных схемах большой размерности. Однако данный подход имеет существенный недостаток - "ручную" подстройку параметров ГА для каждой схемы.

Система GATEST [25.4] ориентирована на последовательностные логические схемы и основана на двухуровневом ГА: на нижнем уровне с помощью ГА строятся входные наборы, а далее ГА применяется для генерации входных последовательностей на основе полученных наборов. Соответственно, на нижнем уровне особью является входной вектор, а на верхнем - входная последовательность. В ГА применяются различные виды операторов кроссинговера: одноточечный, двухточечный, однородный. Первый уровень в свою очередь подразделяется на три фазы. Таким образом, в целом, метод образуют четыре фазы, которые определяют соответствующие различные оценочные функции:

• в фазе 1 целью алгоритма является инициализация триггеров, поэтому оценочная функция определяется как . При этом оценка выполняется с помощью только исправного моделирования;
• в фазе 2 предполагается, что все триггеры установлены, и целью является увеличения покрытия неисправностей полученной последовательностью путем построения новых векторов, обнаруживающих новые неисправности. Оценочная функция для этой фазы имеет вид [25.4]; когда генерируется набор, не обнаруживающий новых неисправностей, алгоритм построения теста переходит в фазу 3, в которой подсчитывается количество новых сгенерированных наборов, не обнаруживающий новых неисправностей. Для стимуляции эволюции входных наборов, тестирующих новые неисправности, в оценочной функции этой фазы учитываются события в исправной и неисправной схемах . Если найден набор, обнаруживающий новые неисправности, то алгоритм возвращается к фазе 2. Иначе при переполнении счетчика неиспользуемых наборов процесс построения теста переходит к фазе 4;
• в фазе 4 выполняется построение тестовых последовательностей на основе полученного множества входных наборов с помощью ГА, оценочная функция определяется как .

В фазах 2-4 оценка особей выполняется с помощью моделирования неисправностей, что несколько замедляет работу GATEST. Система успешно применялась к последовательностным устройствам достаточно большой размерности и строила тесты в тех случаях, где детерминированный метод HITEC [25.1] не мог построить тесты. К недостаткам можно также отнести то, что разработчики вручную подбирают многие параметры ГА, включая размерность алфавита, размер популяции, уровень мутации.

Интересным является подход, представленный в работе [25.7] системой DIGATE. Он состоит из двух фаз:

• в фазе 1 происходит выбор неисправности и ее активизация (то есть распространения до триггеров) с помощью ГА;
• в фазе 2 ищется последовательность, которая сделала бы целевую неисправность наблюдаемой на внешних выходах схемы. Поиск выполняется с помощью ГА путем эволюции различающей последовательности, полученной заранее. Техника, применяемая во второй фазе, является ключевой для данного метода. Объединение двух полученных последовательностей образует тест. Данный подход развит в "Физические дефекты и неисправности " .

В качестве особей, очевидно, используются входные последовательности. Оценка выполняется моделированием неисправностей, при этом оценочные функции представляют собой взвешенные суммы. Соответственно для фазы 1 и 2 оценочные функции имеют следующий вид:

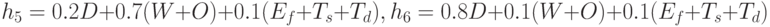
Весовые коэффициенты подобраны разработчиками эвристически для каждой фазы, однако, они универсальны для произвольной схемы. Этим рассмотренный метод выгодно отличается от систем, рассмотренных ранее.

В другой системе [25.5] GATTO в качестве особей также выбраны входные последовательности. Основное внимание авторы алгоритма уделяют определению эффективной оценочной функции, как меры удаленности особи от искомого оптимума. Особи оцениваются с помощью моделирования неисправностей из соображений увеличения активности неисправности в схеме (чем больше количество линий, на которых значения в исправной и неисправной схемах различны, тем больше вероятность обнаружения неисправности). Поэтому оценочная функция определяется тремя эвристическими параметрами: взвешенное количество вентилей с разными значениями в исправном и неисправном устройствах; взвешенное количество триггеров с разными значениями в исправном и неисправном устройствах; длина последовательности-особи, параметр используется для получения компактной тестовой последовательности. В качестве весов первых двух параметров используются соответствующие значения наблюдаемости. Таким образом, оценочная функция есть 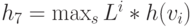, где - особь-последовательность, - -й вектор последовательности, - сумма нормализованных первых двух параметров.

В этом подходе, также как и в предыдущем, отсутствует ручной подбор параметров для отдельной схемы.

В системе АСМИД-Е [25.1] для повышения быстродействия алгоритма построения тестов в программную реализацию интегрированы две программы параллельного моделирования с неисправностями. Первая программа реализует параллельный по неисправностям метод моделирования и используется в фазе 1 для проверки активизации произвольной неисправности случайно генерированной последовательностью.

Для вычисления оценочной функции используется вторая программа моделирования с неисправностями, реализующая алгоритм "параллельного моделирования по тестовым наборам", и написанная специально для работы с генетическим алгоритмом построения тестов. После моделирования очередного тестового вектора происходит вычисление оценочной функции текущего вектора по формул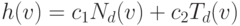е: , где 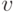- текущий входной набор. В качестве весов используются меры наблюдаемости схемы, вычисляемые на этапе предварительной обработки схемы. После того как для входной последовательности, моделируемой в определённом разряде, достигнута эффективная длина или произведено моделирование на последнем наборе вычисляется оценочная функция всей последовательности:

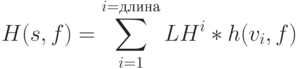
где - анализируемая последовательность; - вектор из рассматриваемой последовательности, - позиция вектора в последовательности, - заданная неисправность, - предварительно заданная константа в диапазоне , благодаря которой предпочтение отдаётся более коротким последовательностям. Применение данного алгоритма существенно повышает скорость вычисления оценочных функций особей в популяции, а, следовательно, и скорость работы алгоритма в целом.

Наиболее эффективным является метод построения тестов, объединяющий преимущества структурного детерминированного и генетического алгоритмов генерации. При этом этапы внесения влияния неисправности и активизации путей до внешних выходов схемы выполняется детерминированным методом с применением многозначных алфавитов, а этап доопределения - поиска значений входов схемы, обеспечивающих требования, полученные на первых этапах, выполняется с помощью ГА. Перспективным является также использование параллельных ГА, в которых используются несколько популяций решений, которые параллельно эволюционируют, в основном, независимо друг от друга. Но время от времени между ними производится обмен лучшими решениями, который может выполняться по различным схемам. Сама природа задачи построения тестов является иерархической, поэтому в ней целесообразно использовать иерархические ГА, где на каждом уровне иерархии применяется свой ГА.