Структурное построение тестов для устройств с памятью

Наиболее распространённым на практике подходом к построению тестов для последовательностных схем является преобразование их в итеративные комбинационные схемы (ИКС), элементом которых является так называемый комбинационный эквивалент (КЭ), и обобщение для них рассмотренных в "Синтез тестов для комбинационных схем" - "Построение тестов с использованием алфавитов большой значности" методов для комбинационных схем.

23.1 Итеративные комбинационные схемы

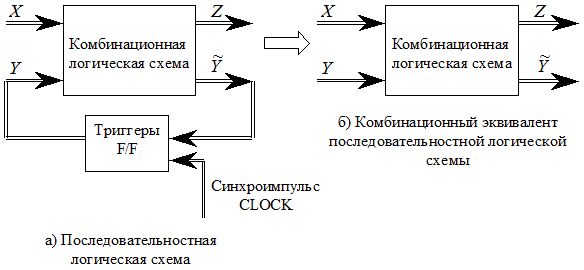
Рис. 23.1. Преобразование последовательностной логической схемы в комбинационный логический эквивалент

Согласно каноническому представлению последовательностное устройство можно представить в виде комбинационного блока и блока памяти, которые соединены линиями обратной связи (рис. 23.1- а, "Модели цифровых устройств" ). Комбинационный эквивалент получается из исходного устройства с памятью путём условного обрыва обратных связей. При этом вектор обратных связей разбивается на вектор так называемых псевдовходов и вектор псевдовыходов (рис. 23.1 - б) [23.1-23.3].

Если рассматривается поведение последовательностной схемы в течение тактов, то комбинационных эквивалентов соединяются последовательно в итеративную комбинационную схему, как показано на рис. 23.2. Здесь произвольная -я итерация итеративной комбинационной схемы соответствует состоянию исходной последовательностной схемы на -м такте времени. При этом компоненты векторов , соответствуют линиям первичных входов и выходов соответственно, 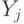, 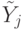- псевдовходам и псевдовыходам соответственно на -м такте. Также очевидно, что 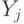, 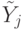- это линии, определяющие состояние последовательностного ЦУ в начале и в конце -го такта соответственно.

Рис. 23.2. Структура комбинационной итеративной схемы из t КЭ

Далее при генерации тестов можно применять один из методов, разработанных для комбинационных схем, с учётом специфики последовательностных. В качестве примера рассмотрим простейший триггер, представленный на рис. 23.3, и его комбинационный эквивалент на рис. 23.4.

Рис. 23.3. Триггер

Рис. 23.4. Комбинационный эквивалент триггера

Рассмотрим построение теста, который проверяет константную неисправность const1 - на нижнем плече триггера на основе методов с использованием шестизначного алфавита , рассмотренных в "Многомерная активизация путей в шестизначном алфавите" , 19.. Процесс построения теста начинается с внесения значения , соответствующего неисправности const 1, в итеративной схеме из одного комбинационного эквивалента, как это показано на рис. 23.5.

Рис. 23.5. Построение тестовой последовательности - 1 КЭ

Из примера видно, что в итеративной комбинационной схеме, как и ранее, надо выполнить распространение критического значения, в данном случае , от места неисправности до внешних выходов схемы при условии неопределенности начального состояния ЦУ, т.е. неопределённых значениях на псевдовходах первого комбинационного эквивалента итеративной комбинационной схемы. Поскольку в процессе доопределения мы получаем для псевдовхода вместо неопределенного значения , то это говорит о невозможности построения теста для итеративной схемы из одного эквивалента (единичной длины). Отметим, что мы строим тест, исходя из предположения, что начальное состояние ЦУ не известно.

Рис. 23.6. Построение тестовой последовательности - 2 КЭ

Поэтому для нашего примера выполняем распространение критического значения на первичный выход для итеративной схемы, содержащей два комбинационных эквивалента (рис. 23.6). В результате этой процедуры и после доопределения значений прямого распространения получаем тестовую последовательность, состоящую из двух наборов:

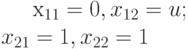
Таким образом, для итеративной комбинационной схемы мы строим не один проверяющий набор, а последовательность входных наборов - тест.

Очевидно, что каждый комбинационный эквивалент в итеративной комбинационной схеме соответствует своему такту или моменту времени. При этом распространение критического значения может произойти как в рамках одного КЭ (т.е. за один такт), так и нескольких КЭ (т.е. за несколько тактов).. Кроме этого, необходимо выполнить, также как и для комбинационных схем, подтверждение значений, полученных в процессе распространения критического значения на первичные выходы. При этом мы получаем значения внешних входов схемы, то есть тестовые наборы.

При внешней простоте и логичности такого подхода существуют принципиальные различия построения тестов для последовательностных и комбинационных ЦУ.

Отметим, что итеративная комбинационная схема в общем случае неадекватно отражает поведение асинхронных последовательностных схем. Строго говоря, эта модель соответствует синхронной последовательностной схеме с синхронизацией в точках обрыва обратных связей. Поэтому полученные при таком подходе результаты для асинхронных схем подлежат дальнейшей проверке, в первую очередь, на предмет отсутствия состязаний сигналов (например, методом Эйхельбергера, изложенным в "Анализ состязаний " ).

Кроме того, при разворачивании последовательностной схемы в итеративную комбинационную неисправности "размножаются". Так, в приведенном примере одиночная константная неисправность на нижнем плече триггера в итеративной комбинационной схеме соответствует двум константным неисправностям и . Поэтому методы генерации тестов для последовательностных схем должны учитывать этот эффект.

При построении тестов производится активизация путей в многозначных алфавитах от неисправных линий до одного из выходов последней -й копии итеративной комбинационной схемы. При этом число копий КЭ определяется условием появления неопределённых значений на псевдовходах -й копии.

При невозможности установить неопределенное значение на псевдовходах возникает проблема установки схемы в заданное начальное состояние. В общем случае надо использовать установочную последовательность, переводящую схему с памятью из неизвестного начального состояния в некоторое известное. Причём эта последовательность должна устанавливать в определённое состояние исправную и неисправную схему.