Выполнимость булевых функций и бинарные диаграммы в построении тестов

21.2 Бинарные диаграммы в генерации тестов

Бинарные диаграммы решений (binary diagrams decisions -BDD), приведенные в "Модели цифровых устройств" , широко применяются в проектировании цифровых систем [21.6,21.7]. В отечественной литературе, кроме термина BDD, также часто используется термин "альтернативные графы"[21.8]. Эта модель применятся также и при решении задач диагностики цифровых систем, в первую очередь, генерации тестов, где пионером является Р.Убар [21.8].

Отметим, что бинарные диаграммы (альтернативные графы - АГ) позволяют представлять ЦУ на различных уровнях[21.8]: 1) структурном, где сохраняется структура исходной логической схемы; 2) функциональном, где структурные соотношения исходной схемы не сохраняются, благодаря чему они имеют меньшую сложность;3) уровне ЯРП, где терминальные вершины могут помечаться переменными, соответствующими регистрам или шинам.

Модель бинарных диаграмм достаточно удобна (и эффективна) при решении многих задач диагностики цифровых систем, таких как:

1. моделирование исправных логических схем в двоичном и многозначных алфавитах;
2. анализ тестов - моделирование неисправностей с оценкой полноты;
3. генерация тестов с использованием процедур распространения влияния неисправностей (fault propagation), подтверждения (justification) и импликации.

В конечном счете, эти задачи сводятся к стандартным процедурам отслеживания (трассировки) или поиска определенных путей на ориентированных графах.

Бинарные диаграммы при решении задачи построения проверяющих тестов можно использовать по-разному, и для этого предложены различные подходы. Наиболее очевидным (прямолинейным) является применение бинарной диаграммы для схемы, которая реализует различающую функцию (исключающее ИЛИ для функций, реализующих исправную и неисправную схемы) [21.2]. Этот подход близок к изложенному в предыдущем разделе методу, основанному на решении задачи выполнимости. Различие в том, что при решении логического уравнения в первом случае используется представление схемы в виде КНФ и методы решения задачи выполнимости, а во втором случае - представление схемы в виде бинарной диаграммы и методы анализа и поиска путей на графах. Рассмотрим этот подход на примере схемы рис. 21.7 [21.2].

Рис. 21.7. Пример схемы для метода бинарной диаграммы.

Рис. 21.8. Приведенная бинарная диаграмма исправной схемы рис. 21.7.

На следующем рис. 21.8 представлена приведенная (сокращенная) бинарная диаграмма для этой исправной схемы. Далее на рис. 21.9 показана бинарная диаграмма этой же схемы с константной неисправностью на третьем сверху входе вентиля . На следующем рис. 21.10 представлена приведенная бинарная диаграмма для различающей функции двух предыдущих схем [21.2]. Детали преобразований можно найти в [21.2].

Рис. 21.9. Приведенная бинарная диаграмма для неисправной схемы.

Рис. 21.10. Приведенная бинарная диаграмма для различающей функции.

Далее необходимо решить логическое уравнение , где различающая функция задана в виде бинарной диаграммы (для нашего примера рис. 21.10). Решение этого уравнению сводится к поиску пути на соответствующем графе, связывающего корень диаграммы (верхний уровень) с единичной вершиной 1 (нижнего уровня). Для нашего примера это может быть путь (1,2,3,4,1), что соответствует значениям входных переменных , , , . В сжатой форме всевозможные значения тестовых наборов, описывающие все пути на бинарной диаграмме, можно представить выражением

Другой подход к построению тестов состоит в том, что генерируются входные наборы, которые активизируют все пути на двоичной диаграмме. Рассмотрим это на примере схемы рис. 21.11 [21.2]. Здесь на рис. 21.11а) показана функциональная бинарная диаграмма, а на рис. 21.11б) схемная реализация этой функции на основе мультиплексоров.

Рис. 21.11. Бинарная диаграмма и ее реализация на основе мультиплексоров.

Для рис. 21.11а) множество значений входных переменных 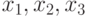, которые активизируют все пути на диаграмме составляют . Отметим, что поскольку генерации теста используется функциональный бинарный граф, который не отражает структурные свойства схемы, то эти тестовые наборы гарантируют проверку константных неисправностей только на внешних входах схемы рис. 21.11б). Этот тест не гарантирует проверку константных неисправностей на внутренних линиях этой схемы.

Отметим, что модель бинарных диаграмм позволяет использовать следующие модели неисправностей, которые ориентированы непосредственно на эту модель [21.9]:

• дуга узла всегда активна;
• обрыв дуги узла;
• вместо данной дуги активна другая дуга (или множество дуг).

В этих моделях "ломается" не схема, а представляющая ее бинарная диаграмма. Это приводит к появлению и изменению путей в соответствующем графе. Известны работы, где бинарные диаграммы и подобные модели применяются при построении тестов микропроцессорных систем [21.9,21.10].

В [21.10] предложен также подход, основанный на покрытии путей в бинарной диаграмме. Основу теста здесь составляют 0-эксперименты (пути из корневой вершины в нулевую вершину) и 1-эксперименты (пути из корневой вершины в единичную вершину). Например, для бинарной диаграммы рис. 21.12 [21.2] 0-эксперименты составляют , где значения приведены в порядке входных переменных 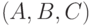. Аналогично 1-эксперимент составляют . На рис. 21.12 видно, что 1-эксперименты активизируют соответствующие пути, заканчивающиеся в нулевой или единичной выходной вершине. Напомним, что "жирная" точка на диаграмме соответствует инверсии значения.

Рис. 21.12. Пример бинарной диаграммы для 0-,1-экспериментов.

Авторы [21.10] при построении теста рассматривают так называемые "боковые эффекты" текущего эксперимента, в которые входят другие эксперименты, чьи выходные значения противоположны текущему и некотрые позиции отличны от исходного эксперимента. Например, для текущего 1-эксперимента ожидаемый выход равен 0. Тогда в "боковой эффект" входит эксперимент . Это означает, что константная неисправность вызывает 1 на выходе. С другой стороны для текущего 0-эксперимента ожидаемый выход равен 0. В этом случае в "боковой эффект" входит експеримент поскольку изменяет 0-ребро из B на 1-ребро . Тогда при константной неисправности выход равен 1, что говорит об ее обнаружении.