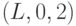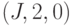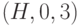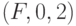|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Методы генерации тестов PODEM, FAN и SOCRATES
Рассмотрим работу метода FAN на примере схемы рис. 19.8. Здесь входы  ,
, являются внешними, в то время как
являются внешними, в то время как  ,
,  ,
,  и
и  соединены с выходами подсхем и имеют худшие показатели управляемости. Результаты работы FAN-алгоритма представлены в табл. 19.3[19.3].
Алгоритм стартует с начальными целями
соединены с выходами подсхем и имеют худшие показатели управляемости. Результаты работы FAN-алгоритма представлены в табл. 19.3[19.3].
Алгоритм стартует с начальными целями  ,
,  и
и  . Отметим, что в узле разветвления S суммирование значений схем
. Отметим, что в узле разветвления S суммирование значений схем  и
и  дает
дает 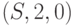 . Аналогично триплеты
. Аналогично триплеты  и
и  дают триплет
дают триплет 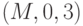 . Это требует установки значения 0 на одном из входов
. Это требует установки значения 0 на одном из входов  .
Для удобства предположим, что
.
Для удобства предположим, что  имеет лучший показатель управляемости. Поскольку вентиль
имеет лучший показатель управляемости. Поскольку вентиль  инвертирующего типа, то значения
инвертирующего типа, то значения  и
и  триплета меняются местами.
Таким образом, выполняется обратное распространение через каждый логический элемент, в результате чего мы достигаем узла разветвления
триплета меняются местами.
Таким образом, выполняется обратное распространение через каждый логический элемент, в результате чего мы достигаем узла разветвления  . Здесь имеет место конфликтная ситуация, поскольку оба значения
. Здесь имеет место конфликтная ситуация, поскольку оба значения  и
и  не равны нулю. Поскольку ветвь
не равны нулю. Поскольку ветвь 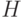 имеет больший вес, то при разрешении конфликта мы в качестве первого варианта принимаем значение
имеет больший вес, то при разрешении конфликта мы в качестве первого варианта принимаем значение  .
Поскольку
.
Поскольку  является головным элементом подсхемы, то присваивание значений входам
является головным элементом подсхемы, то присваивание значений входам  и
и  откладывается. Присвоенное значение
откладывается. Присвоенное значение  вызывает конфликт на линии
вызывает конфликт на линии  , где значение
, где значение  обусловлено целью
обусловлено целью  . Но эта цель может быть достигнута путем присваивания
. Но эта цель может быть достигнута путем присваивания  , что позволяет разрешить конфликт на
, что позволяет разрешить конфликт на  .
Если бы конфликт не удалось разрешить вследствие невозможности присваивания
.
Если бы конфликт не удалось разрешить вследствие невозможности присваивания  , мы были бы вынуждены рассмотреть альтернативный вариант для узла разветвления
, мы были бы вынуждены рассмотреть альтернативный вариант для узла разветвления  . В этом случае конфликт можно разрешить путем присваивания
. В этом случае конфликт можно разрешить путем присваивания 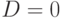 . При этом ответствующие триплеты должны быть вычислены заново. После разрешения конфликта процедура продвижения назад MBack выбирает узел разветвления, который определяет новые текущие цели.
. При этом ответствующие триплеты должны быть вычислены заново. После разрешения конфликта процедура продвижения назад MBack выбирает узел разветвления, который определяет новые текущие цели.
В заключение рассмотрим укрупненный алгоритм метода FAN [19.3] в виде псевдокода, который представлен на рис. 19.9 в конце настоящего раздела. Здесь, прежде всего, выполняется активизация неисправности путем присваивания соответствующего значения  или
или  на неисправной линии. Далее устанавливается значение признака
на неисправной линии. Далее устанавливается значение признака 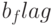 , который позволяет процедуре продвижения назад MBack различать случаи, когда она стартует из множества начальных целей (
, который позволяет процедуре продвижения назад MBack различать случаи, когда она стартует из множества начальных целей ( ), или множества целей, соответствующим узлам разветвления (
), или множества целей, соответствующим узлам разветвления (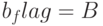 ).
Второй вариант встречается, когда процедура продолжает распространение назад от узла разветвления. Далее выполняется D-распространение от неисправной линии до одного из внешних выходов схемы. При распространении
).
Второй вариант встречается, когда процедура продолжает распространение назад от узла разветвления. Далее выполняется D-распространение от неисправной линии до одного из внешних выходов схемы. При распространении  -значения через логический элемент его соседним входам присваиваются не блокирующие значения ( 1(0) для И (ИЛИ) ), которые заносятся в множество начальных целей.
Если
-значения через логический элемент его соседним входам присваиваются не блокирующие значения ( 1(0) для И (ИЛИ) ), которые заносятся в множество начальных целей.
Если  -граница содержит два или более элемента, то FAN исследует эти элементы на приемлемость - допускают ли они
-граница содержит два или более элемента, то FAN исследует эти элементы на приемлемость - допускают ли они  -распространение (выполняется проверка на наличие блокирующих значений соседних входов элементов). Далее FAN производит упорядочение возможных путей
-распространение (выполняется проверка на наличие блокирующих значений соседних входов элементов). Далее FAN производит упорядочение возможных путей  -распространения в соответствии с показателями наблюдаемости. Отметим, что подобно
-распространения в соответствии с показателями наблюдаемости. Отметим, что подобно  - алгоритму данный метод в случае необходимости выполняет одномерную и многомерную активизацию (
- алгоритму данный метод в случае необходимости выполняет одномерную и многомерную активизацию ( -распространение).
-распространение).
Входной параметр процедуры обратного распространения MBack имеет два значения :  и
и  . Значение A соответствует случаю, когда множество текущих целей
. Значение A соответствует случаю, когда множество текущих целей  не пусто. В этом случае производится выбор цели.
В процессе обратного распространения в случае достижения головной линии (head) она добавляется во множество головных целей
не пусто. В этом случае производится выбор цели.
В процессе обратного распространения в случае достижения головной линии (head) она добавляется во множество головных целей  . При обратном проходе через логический элемент прежде всего необходимо определить какие значения - контролирующие или неконтролирующие необходимо присвоить его входам. Как сказано выше, правила, приведенные в табл. 19.2 позволяют выбрать вход и логическое значение. Схема, которая питает этот вход, добавляется во множество текущих целей {СО}. При достижении узла разветвления значения
. При обратном проходе через логический элемент прежде всего необходимо определить какие значения - контролирующие или неконтролирующие необходимо присвоить его входам. Как сказано выше, правила, приведенные в табл. 19.2 позволяют выбрать вход и логическое значение. Схема, которая питает этот вход, добавляется во множество текущих целей {СО}. При достижении узла разветвления значения  и
и  изменяются.
изменяются.
Значение  входного параметра процедуры MBack используется, если множество текущих целей пусто. В этом случае узел разветвления FPO выбирается из множества целей
входного параметра процедуры MBack используется, если множество текущих целей пусто. В этом случае узел разветвления FPO выбирается из множества целей  . Однако, если выбранная цель содержит конфликт, то он должен быть разрешен. Это производится путем возврата к выбору других значений для данного узла разветвления.
. Однако, если выбранная цель содержит конфликт, то он должен быть разрешен. Это производится путем возврата к выбору других значений для данного узла разветвления.
При инициализации признак 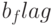 устанавливается в 1, если по окончании фазы импликации остались неподтвержденные значения в схеме. В этой точке все множества целей инициализируются (присваивается пустое множество) и производится сброс флага
устанавливается в 1, если по окончании фазы импликации остались неподтвержденные значения в схеме. В этой точке все множества целей инициализируются (присваивается пустое множество) и производится сброс флага 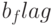 .
Если есть неподтвержденные линии, то они образуют множество начальных целей
.
Если есть неподтвержденные линии, то они образуют множество начальных целей  . Если
. Если  -значение не достигает внешнего выхода, элемент из
-значение не достигает внешнего выхода, элемент из  -границы добавляется в
-границы добавляется в  . Как уже отмечалось алгоритм обратного распространения реализуется в MBack.
Если
. Как уже отмечалось алгоритм обратного распространения реализуется в MBack.
Если 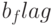 не установлен в 1, то нет неподтвержденных линий, которые ожидают присвоения значений. В этом случае исследуется множество целей, соответствующих узлам разветвлений
не установлен в 1, то нет неподтвержденных линий, которые ожидают присвоения значений. В этом случае исследуется множество целей, соответствующих узлам разветвлений  . Если оно не пусто, то обратное распространение выполняется от выбранного узла разветвления. По завершению кратного распространения назад в случае отсутствия конфликтов на узлах разветвления обрабатывается множество головных целей {HO}.Если есть конфликт на узле разветвления (оба значения
. Если оно не пусто, то обратное распространение выполняется от выбранного узла разветвления. По завершению кратного распространения назад в случае отсутствия конфликтов на узлах разветвления обрабатывается множество головных целей {HO}.Если есть конфликт на узле разветвления (оба значения  и
и  не равны нулю), то, как неоднократно отмечалось, присваивается значение с большим весом.
не равны нулю), то, как неоднократно отмечалось, присваивается значение с большим весом.
FAN() / / аргументы -номер элемента и линии с константной неисправностью
{
инициализация неисправности; // присваивание D или D' неисправной линии
b_flag=A; //режим обратного распространения от неподтвержденных линий
for(::) //основной цикл
{
импликация; //прямая и обратная
if(необходимо обратное распространение)
b_flag=B; // обработка разветвлений
if(значение D достигло внешнего выхода) {
if(число неподтвержденных линий==0) {
подтверждение свободных линий;
return(тест);
}
else{
конечная_цель();
присваивание значений линиям конечной цели;
}
}
else {
if(число элементов в D-границе >1) {
//выбор вентиля, ближайшего к выходу
конечная_цель();
присваивание значений линиям конечной цели;
}
else if(число вентилей в D-границе ==1)
одномерная активизация;
else { //число вентилей ==0
if (есть нерассмотренные варианты) {
установка нерассмотренного варианта;
b_flag=B;
}
else
return (нет теста);
}
}
}
}
конечная_цель()
{
mb = 0:
if(b_flag==A)
mb=Mback(A);
else if (множество целей разветвлений не пусто)
mb=Mback(A);
if (mb==D) {
конечная_цель=FPO; //узел разветвления
return;
}
for(;;)
{
if (множество головных целей пусто)
mb=Mback(A);
выбор головной цели;
if(головная линия не определена)
break;
}
головная цель= конечная цель;
}
Mback(flag)
{
if(flag==A) {
b_flag=0;
if (число неподтвержденных линий>0)
{Начальная цель} =неподтвержденные линии;
if(D-значение не достигло внешнего выхода)
добавить элемент в D-границе в начальные цели;
{текущая_цель}={начальная_цель};
if({текущая_цель} не пусто) {
выбор текущей цели;
следущая_цель();
}
else {
if (FPO ==пусто)
return(C);
else
flag=B;
}
}
if (flag==B) {
выбор узла разветвления, ближайшего к внешнему выходу;
if (p достижимо от неисправной линии) или ( (n_{0}==0) или (n_{1}==0) )
следующая_цель();
else
return(D):
}
}
следующая_цель()
{
if (текущая_цель==головная линия)
добавить текущую_цель в головные цели;
else if (текущая_цель питается узлом разветвления)
добавить n_{0} и n_{1} к FPO //согласно правилу 10 табл. 19.2
else // определить следующую цель
распространение назад согласно правилам табл. 19.2
}