Синтез тестов для заданной неисправности

17.3 Метод активизации одномерного пути

Основная идея этого метода заключается в выборе и активизации пути от места неисправности через последовательность вентилей до некоторого внешнего выхода [17.3]. Этот процесс выполняется в три этапа [17.4]:

1. Активизация (sensitization) неисправности, при которой на неисправную линию подается сигнал, противоположный неисправному значению.
2. Распространение (propagation) неисправности от места неисправности до одного из внешних выходов.
3. Доопределение (justification) необходимых для активизации и распространения значений сигналов.

На втором этапе соседним входам вентилей, вошедших в активизированный путь, присваиваются такие значения сигналов, при которых выход вентиля зависит от входа, входящего в этот активизированный путь. Таким образом, для элементов типа И, НЕ-И соседние входы получают значение 1, а для ИЛИ, НЕ-ИЛИ соседние входы получают значение 0. Иногда этот этап называют прямой фазой, а выбранный путь - активизированным путём.

Выбрав и установив активизированный путь на третьем этапе необходимо найти значения сигналов на внешних входах схемы, которые дают требуемые значения на входах вентилей активизированного пути. Для этого по схеме прослеживаются необходимые значения сигналов до внешних входов схемы. Этот процесс иногда называют обратной фазой. Рассмотрим этот простой метод на примере построения теста для неисправности схемы, представленной на рис. 6.5.

Рис. 17.3. Одномерная активизация путей

Выполняем первый этап - активизацию неисправности. Очевидно, в исправной схеме необходимо получить (значение сигнала, противоположное неисправности), что обеспечивается значением внешнего входа . Далее выбираем (произвольно) путь , , от места неисправности до выхода схемы . Необходимым условием активизации этого пути является равенство значений сигналов соседних входов, обеспечивающих распространение влияния неисправности: для активизации пути от к ; для активизации пути от к ; для активизации пути от к .

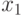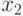Этим завершается прямая фаза (этап активизации). Далее необходимо найти значения внешних входов схемы, обеспечивающие полученные на предыдущем этапе условия распространения влияния неисправности. В данном случае надо найти значения и , обеспечивающие равенство . Из трех возможных комбинаций выбираем , . В результате получаем тестовый набор , , , , . Когда этот набор подается на схему, то выход схемы при наличии неисправности и при ее отсутствии. Следовательно, построенный входной набор действительно является тестовым.

Отметим, что при выполнении этапа подтверждения (обратной фазы) возможен перебор различных вариантов значений входных сигналов и неудачный выбор может привести в дальнейшем к несовместимости полученных значений сигналов на некоторых линиях схемы. В этом случае необходимо "дать задний ход" и выполнить перебор других вариантов до тех пор, пока несовместимость не будет устранена. Таким образом, задача построения теста для заданной неисправности носит переборный характер.

Рис. 17.4. Контрпример для метода одномерной активизации.

К сожалению, рассмотренный метод не является алгоритмом, т.е. он не гарантирует построение теста для отдельных неисправностей некоторых схем. Например, для приведённой на рис. 17.4 схемы для неисправности этот метод не может построить тест.

Активизация одиночного пути 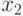, , требует значения , что невозможно, так как для активизации неисправности необходимо подать , что ведет к требованию 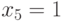(т.е. возникновению противоречия - конфликта на линии 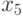). В силу симметрии невозможно также активизировать второй одиночный путь 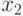, , 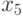. Тем не менее, тест для этой неисправности существует - , , . Действительно, на этом наборе при отсутствии неисправности и при ее наличии. Этот тест не может быть построен данным методом, так как в этом случае необходимо активизировать одновременно два пути от места неисправности до внешнего выхода схемы. Все последующие методы построения тестов основаны на многомерной активизации (нескольких) путей с использованием многозначных алфавитов.

Ключевые термины:

Различающая функция - определяет множество входных наборов, на которых исправная и неисправная схема дают различные выходные реакции.

Булева производная - определяет зависимость булевой функции от переменной.

Активизация пути - обеспечивает распространение различия значений сигналов в исправной и неисправной схеме от места неисправности до внешнего выхода схемы.

Краткие итоги

В лекции рассмотрена задача построения проверяющего теста для конкретной заданной неисправности комбинационной схемы. Изложены аналитические методы построения тестов для заданной неисправности.

В "Синтез тестов для заданной неисправности" показано, что задача генерации проверяющего теста для заданной неисправности комбинационной схемы может быть решена аналитически путем построения различающей функции, что позволяет ее свести к решению булева уравнения.

В "Синтез тестов для заданной неисправности" изложен метод булевых производных, который является развитием метода различающей функции. Рассматриваются свойства булевых производных и их применение к задаче построения тестов.

В "Синтез тестов для заданной неисправности" описан простейший структурный метод построения тестов, основанный на активизации одномерных путей в комбинационной схеме, которые обеспечивают распространение различий сигналов исправной и неисправной схем от места неисправности до внешнего выхода.

Вопросы и упражнения

1. Каким образом задача построения теста для заданной неисправности может быть сформулирована аналитически?
2. Приведите определение различающей функции.
3. Как из различающей функции получить входные тестовые наборы?
4. Постройте методом различающей функции проверяющий тест для неисправности const0 на выходе второго вентиля первого уровня, приведенной на рис. 17.5.
   

   
   Рис. 17.5. Схема для упражнения 4.
5. Дайте определение булевой производной.
6. Приведите основные свойства булевых производных.
7. Как булеву производную можно использовать при построении тестовых наборов для заданной неисправности?
8. Какое булево уравнение необходимо решить для построения теста для неисправности константа 0?
9. Какое булево уравнение необходимо решить для построения теста для неисправности константа 1?
10. Постройте методом булевой производной проверяющий тест для неисправности , приведенной на рис. 17.6.
    

    
    Рис. 17.6. Схема для упражнения 10.
11. Опишите этапы одномерной активизации пути.
12. Постройте методом активизации путей проверяющий тест для неисправности , приведенной на схеме рис. 17.6.
    

    
    Рис. 17.7. Схема для упражнения 12.