|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Моделирование неисправностей задержек распространения сигналов
14.3 Моделирование задержек на основе многозначных логик
В работах [14.1,14.3] для анализа неисправностей типа "задержка распространения сигнала" использовалась шестизначная логика (которая также кратко будет рассмотрена в конце данного раздела). Мы, в основном будем использовать следующее подмножество  универсального алфавита
универсального алфавита
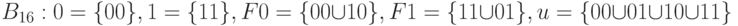
При анализе задержек распространения сигналов на паре  переменных внешних входов, изменяющихся
переменных внешних входов, изменяющихся 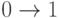 (передний фронт) присвоим значение
(передний фронт) присвоим значение  . Аналогично переменным, с изменением
. Аналогично переменным, с изменением 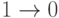 (задний фронт) припишем
(задний фронт) припишем  .
Переменные входов, сохраняющие значения на этой паре наборов, получают значения 0 и 1 соответственно. После присваивания значений переменным внешних входов следует выполнить моделирование в алфавите
.
Переменные входов, сохраняющие значения на этой паре наборов, получают значения 0 и 1 соответственно. После присваивания значений переменным внешних входов следует выполнить моделирование в алфавите  . Например, для пары наборов
. Например, для пары наборов  рис. 14.1 результат моделирования в алфавите
рис. 14.1 результат моделирования в алфавите  приведен на том же рисунке.
Очевидно, линии схемы, получившие значения
приведен на том же рисунке.
Очевидно, линии схемы, получившие значения  и
и  , являются кандидатами на включение их в пути, проверяемые данной парой наборов на неисправности типа задержка сигнала. Чтобы точно определить проверяемые пути, необходимо найти пути в схеме, начинающиеся на внешних входах и заканчивающиеся на внешних выходах, все линии которых имеют значения
, являются кандидатами на включение их в пути, проверяемые данной парой наборов на неисправности типа задержка сигнала. Чтобы точно определить проверяемые пути, необходимо найти пути в схеме, начинающиеся на внешних входах и заканчивающиеся на внешних выходах, все линии которых имеют значения  или
или  и удовлетворяющие указанным выше условиям.
и удовлетворяющие указанным выше условиям.
Таким образом, пара  является неустойчивым тестом для пути
является неустойчивым тестом для пути  (здесь
(здесь  - внешний вход, а
- внешний вход, а 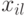 - внешний выход схемы) если при моделировании в алфавите
- внешний выход схемы) если при моделировании в алфавите 
 или
или  для
для  и
и  .
.
Отметим, что проверка условия  для основных вентилей выполняется достаточно просто: для вентилей типа ИЛИ, НЕ-И входы, не принадлежащие пути
для основных вентилей выполняется достаточно просто: для вентилей типа ИЛИ, НЕ-И входы, не принадлежащие пути  , должны быть равны 1; для вентилей типа ИЛИ, НЕ-ИЛИ - 0.
Например, для пути
, должны быть равны 1; для вентилей типа ИЛИ, НЕ-ИЛИ - 0.
Например, для пути  рассматриваемого примера, пара
рассматриваемого примера, пара  является неустойчивым тестом, так как выполняются вышеприведенные условия. Проверка устойчивости теста также достаточно проста и заключается в следующем. Можно показать, что для вентилей типа И, НЕ-И при распространении переднего фронта (
является неустойчивым тестом, так как выполняются вышеприведенные условия. Проверка устойчивости теста также достаточно проста и заключается в следующем. Можно показать, что для вентилей типа И, НЕ-И при распространении переднего фронта ( ) остальные входы, не принадлежащие пути, должны иметь значения 1 или
) остальные входы, не принадлежащие пути, должны иметь значения 1 или  . Для заднего фронта (
. Для заднего фронта ( остальные входы должны быть равны только 1. Аналогично для вентилей типа ИЛИ, НЕ-ИЛИ при переднем фронте остальные входы должны иметь значения 0, а при заднем - значения 0 или
остальные входы должны быть равны только 1. Аналогично для вентилей типа ИЛИ, НЕ-ИЛИ при переднем фронте остальные входы должны иметь значения 0, а при заднем - значения 0 или  . Например, для пути
. Например, для пути 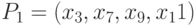 эти условия выполняются. Достаточность этих условий вытекает из следующих рассуждений. Рассмотрим вентили
эти условия выполняются. Достаточность этих условий вытекает из следующих рассуждений. Рассмотрим вентили  типа И, НЕ-И.
Если на некоторый вход
типа И, НЕ-И.
Если на некоторый вход  приходит изменение сигнала, то из условия
приходит изменение сигнала, то из условия
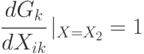
следует, что остальные входы должны иметь значения  или
или  . Если это изменение образует передний фронт
. Если это изменение образует передний фронт  , то остальные входы вентиля могут принимать любое из значений (1 или
, то остальные входы вентиля могут принимать любое из значений (1 или  ), так как задержка переднего фронта
), так как задержка переднего фронта  на этих входах не может компенсировать задержку переднего фронта на входе
на этих входах не может компенсировать задержку переднего фронта на входе  и будет проявляться на выходе вентиля
и будет проявляться на выходе вентиля  . B случае заднего фронта на входе
. B случае заднего фронта на входе  , а остальные входы должны быть равны 1, так как задержка переднего фронта
, а остальные входы должны быть равны 1, так как задержка переднего фронта  на любом другом входе может привести к компенсации задержки заднего фронта на входе
на любом другом входе может привести к компенсации задержки заднего фронта на входе  . Аналогично можно показать достаточность соответствующих условий и для вентилей типа ИЛИ, НЕ-ИЛИ.
. Аналогично можно показать достаточность соответствующих условий и для вентилей типа ИЛИ, НЕ-ИЛИ.
Таким образом, моделирование пары наборов 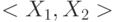 в алфавите
в алфавите  с последующей проверкой достаточных условий позволяет выявить неисправности типа задержка распространения сигналов по путям схемы, проверяемые данной парой.
Более того, функции
с последующей проверкой достаточных условий позволяет выявить неисправности типа задержка распространения сигналов по путям схемы, проверяемые данной парой.
Более того, функции  позволяют проводить параллельно моделирование множества пар наборов, что существенно повышает эффективность метода. В этом случае мы имеем аналог метода PPSF для неисправностей типа задержка распространения сигналов. Из всего вышесказанного следует, что универсальная модель функций
позволяют проводить параллельно моделирование множества пар наборов, что существенно повышает эффективность метода. В этом случае мы имеем аналог метода PPSF для неисправностей типа задержка распространения сигналов. Из всего вышесказанного следует, что универсальная модель функций  , введенная в
"Система многозначных алфавитов и функций"
, позволяет эффективно решать и этот класс задач, весьма важный для современных ДУ.
, введенная в
"Система многозначных алфавитов и функций"
, позволяет эффективно решать и этот класс задач, весьма важный для современных ДУ.
В заключение отметим, что используемая в некоторых работах [14.1,14.4] шестизначная логика для моделирования рассмотренных неисправностей, функционирование в которой вентиля И представлено в табл. 14.1, может быть получена из универсальной 16-значной логики следующим образом.
Ее алфавит  образует подмножество
образует подмножество 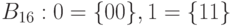 ,
,  ,
,
 ,
,
 ,
,
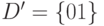 . Но для моделирования в алфавите
. Но для моделирования в алфавите  согласно табл. 14.1 необходимо скорректировать функции
согласно табл. 14.1 необходимо скорректировать функции  . Так для вентиля И в функции
. Так для вентиля И в функции  надо добавить один терм
надо добавить один терм 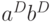 .
.
Аналогично для вентиля ИЛИ в функции 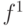 необходимо добавить терм
необходимо добавить терм  . Таким образом скорректированные функции имеют вид:
. Таким образом скорректированные функции имеют вид:
- для вентиля И -

- для вентиля ИЛИ -
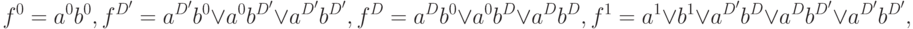
B [14.1] показано, что данная логика позволяет моделировать неисправности типа задержка распространения сигналов. Это выполняется путем приписывания входам с передним (задним) фронтом значений  и моделирования в алфавите
и моделирования в алфавите  . Пути от внешних входов до внешних выходов схемы, состоящие из линий со значениями
. Пути от внешних входов до внешних выходов схемы, состоящие из линий со значениями  или
или  устойчиво проверяются данной парой наборов. Здесь расширение алфавита дает возможность обойтись без проверки дополнительных условий. Отметим, что скорректированные функции
устойчиво проверяются данной парой наборов. Здесь расширение алфавита дает возможность обойтись без проверки дополнительных условий. Отметим, что скорректированные функции  также дают возможность моделировать параллельно группу наборов. Как правило, для проверки задержек распространения сигналов используют пары соседних наборов, отличающиеся значениями сигналов только для одного входа. Вопросы построения проверяющих тестов для этих неисправностей будут рассмотрены в следующей главе.
также дают возможность моделировать параллельно группу наборов. Как правило, для проверки задержек распространения сигналов используют пары соседних наборов, отличающиеся значениями сигналов только для одного входа. Вопросы построения проверяющих тестов для этих неисправностей будут рассмотрены в следующей главе.
Ключевые термины:
Задержка - уменьшение времени распространения сигнала.
Устойчивый тест - проверяет данную неисправность независимо от других неисправностей типа задержка сигнала.
Неустойчивый тест - проверяет данную неисправность приопределенных условиях.
Шестизначная логика - используется для моделирования задержек и содержит 6 символов.
Краткие итоги
В лекции рассмотрены проблемы моделирования неисправностей "задержка", которые вызывают задержку распространения сигналов.
В "Моделирование неисправностей задержек распространения сигналов" вводится понятие неисправности "задержка распространения сигнала".
В "Моделирование неисправностей задержек распространения сигналов" вводится понятие устойчивого и неустойчивого теста для проверки неисправности "задержка".
"Моделирование неисправностей задержек распространения сигналов" посвящен моделированию неисправностей "задержка" с применением многозначных логик.
Вопросы и упражнения
- Что такое неисправность "задержка распространения сигнала"?
- Дайте определение устойчивого теста для неисправности "задержка".
- Дайте определение неустойчивого теста для неисправности "задержка".
- Какое подмножество универсального 16-значного алфавита можно использовать для моделирования неисправностей "задержка".
- Как используется 6-значная логика для моделирования неисправности "задержка".


