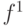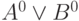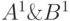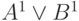|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Последовательное и параллельное моделирование неисправностей
Данные моделирования этой схемы для одного входного набора ( ) приведены в табл. 11.1, где строки таблицы соответствуют линиям этой схемы - машинным словам), а столбцы (биты) - моделируемым неисправным схемам. При этом в левом столбце приведены имена линий схемы (и логические выражения для внутренних линий), во втором слева столбце логические значения исправной схемы для каждой линии, и последующих столбцах (разрядах машинных слов) значения сигналов для каждой неисправной схемы. Например, третий слева столбец представляет значения сигналов на моделируемом входном наборе для схемы с неисправностью
) приведены в табл. 11.1, где строки таблицы соответствуют линиям этой схемы - машинным словам), а столбцы (биты) - моделируемым неисправным схемам. При этом в левом столбце приведены имена линий схемы (и логические выражения для внутренних линий), во втором слева столбце логические значения исправной схемы для каждой линии, и последующих столбцах (разрядах машинных слов) значения сигналов для каждой неисправной схемы. Например, третий слева столбец представляет значения сигналов на моделируемом входном наборе для схемы с неисправностью 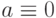 . Очевидно, что для определения множества проверяемых неисправностей достаточно сравнить значения сигналов в последней строке, которая соответствует внешнему выходу схемы
. Очевидно, что для определения множества проверяемых неисправностей достаточно сравнить значения сигналов в последней строке, которая соответствует внешнему выходу схемы  . Поскольку исправная схема (второй столбец) имеет на внешнем выходе
. Поскольку исправная схема (второй столбец) имеет на внешнем выходе  , то проверяются все неисправности, для которых
, то проверяются все неисправности, для которых  :
:  .
.
Мы рассмотрели пример параллельного моделирования схемы на одном тестовом наборе. Для моделирования на тестовой входной последовательности эту процедуру надо выполнить для каждого тестового набора. При этом аналогичным образом определяются неисправности, проверяемые на наборе. Неисправности, проверяемые всей тестовой последовательностью, находятся путём объединения всех неисправностей, проверяемых на каждом тестовом наборе.
11.4 Параллельное моделирование в троичном алфавите
При параллельном методе моделирования можно использовать различные виды кодирования троичного алфавита  , которые были представлены в
"Модели логических элементов"
. Рассмотрим для определенности дизъюнктивный метод кодирования, представленный в табл. 11.2. Напомним, что здесь каждая троичная переменная
, которые были представлены в
"Модели логических элементов"
. Рассмотрим для определенности дизъюнктивный метод кодирования, представленный в табл. 11.2. Напомним, что здесь каждая троичная переменная 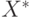 представлена двумя двоичными переменными
представлена двумя двоичными переменными  и
и 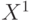 .
Соответственно моделирование одного вентиля в троичном алфавите выполняется с помощью двух булевых функций - компонент
.
Соответственно моделирование одного вентиля в троичном алфавите выполняется с помощью двух булевых функций - компонент  ,
,  , приведенных в табл. 11.3. При этом, например, моделирование вентиля И
, приведенных в табл. 11.3. При этом, например, моделирование вентиля И  в троичном алфавите согласно табл.11. выполняется с помощью двух логических операций:
в троичном алфавите согласно табл.11. выполняется с помощью двух логических операций:  ,
,
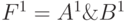 .
Таким образом, фактически моделирование одного вентиля в троичном алфавите, как бы, заменяется моделированием двух вентилей в двоичном алфавите, что показано на рис. 11.4.
.
Таким образом, фактически моделирование одного вентиля в троичном алфавите, как бы, заменяется моделированием двух вентилей в двоичном алфавите, что показано на рис. 11.4.
Допустим, что выполняется параллельное моделирование с 4-разрядными машинными словами. Пусть входы вентиля имеют текущие значения из троичного алфавита  ,
,  . Тогда с учетом дизъюнктивного кодирования имеем:
. Тогда с учетом дизъюнктивного кодирования имеем:

Пусть в левом разряде моделируется исправная схема, во 2-м разряде - неисправность  , в 3-м разряде -
, в 3-м разряде -  , в 4-м разряде -
, в 4-м разряде - и в 5-м разряде -
и в 5-м разряде -  . Тогда после внесения влияния неисправностей на входах имеем:
. Тогда после внесения влияния неисправностей на входах имеем:
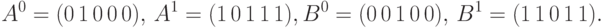
После выполнения логических операций
 ,
,
 и внесения неисправности выхода вентиля получаем:
и внесения неисправности выхода вентиля получаем:
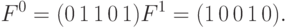
Очевидно при переходе к троичному алфавиту затраты оперативной памяти возрастают в 2 раза, так как каждой линии схемы соответствует два машинных слова. Быстродействие уменьшается в два раза, так как вместо одной логической операции для стандартных вентилей согласно табл. 11.3 выполняется две операции.
Иногда число проходов ![]N/P-1[](/sites/default/files/tex_cache/ba3e05bdd4e7e3e22687fabbe3ca321a.png) , необходимое при параллельном методе удается несколько уменьшить за счет того, что несколько независимых неисправностей могут моделироваться в одном и том же разряде. При этом неисправности должны располагаться на линиях схемы, не влияющих друг на друга.
, необходимое при параллельном методе удается несколько уменьшить за счет того, что несколько независимых неисправностей могут моделироваться в одном и том же разряде. При этом неисправности должны располагаться на линиях схемы, не влияющих друг на друга.
Существенным ограничением параллельного метода моделирования является то, что при нем функционирование логических элементов должно быть описано с помощью булевых функций. Это связано с тем, что основной выигрыш во времени при этом методе получается путем выполнением логических операций, которые в компьютере реализуются параллельно над всеми разрядами машинных слов. Если же элемент описан на функциональном уровне, то каждую сложную функцию или оператор языка регистровых передач надо описать с помощью булевых функций, что увеличивает сложность модели.
Следует отметить, что параллельный метод использует, как правило, модель нулевой или единичной задержки логических элементов. Модель задержки с разными значениями для переднего и заднего фронтов также не может быть использована, так как в различных разрядах здесь моделируются различные неисправные схемы, в которых на одной и той же линии могут быть различные фронты изменения сигналов.
11.5 Параллельное моделирование в многозначных алфавитах
До недавнего времени в многозначных алфавитах (со значностью больше 4) этот метод распространения не получил, так как при увеличении значности алфавита резко падает скорость моделирования в виду сложности многозначных моделей логических элементов.
Метод кодирования и единая система моделей на базе четырех компонент  позволяют существенно повысить скорость параллельного метода моделирования в многозначных алфавитах и сделать ее приемлемой для практического применения. При параллельном методе моделирования влияние неисправностей распространяется параллельно для группы
позволяют существенно повысить скорость параллельного метода моделирования в многозначных алфавитах и сделать ее приемлемой для практического применения. При параллельном методе моделирования влияние неисправностей распространяется параллельно для группы 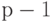 неисправностей (
неисправностей ( - разрядность инструментальной ЭВМ).
При этом каждой линии схемы ставится в соответствие несколько машинных слов, число которых определяется количеством компонент в применяемом методе кодирования многозначных алфавитов. Для кодирования, представленного в табл. 7.1 , каждой линии схемы ставится в соответствие четыре машинных слова, как это показано на рис. 11.5.
При моделировании логических элементов (в данном случае конъюнкции
- разрядность инструментальной ЭВМ).
При этом каждой линии схемы ставится в соответствие несколько машинных слов, число которых определяется количеством компонент в применяемом методе кодирования многозначных алфавитов. Для кодирования, представленного в табл. 7.1 , каждой линии схемы ставится в соответствие четыре машинных слова, как это показано на рис. 11.5.
При моделировании логических элементов (в данном случае конъюнкции 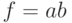 ) используются функции
) используются функции  . На рис. 11.5 приведены закодированные значения
. На рис. 11.5 приведены закодированные значения  ,
, 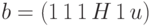 , из которых согласно функциям
, из которых согласно функциям  для этого вентиля получаем значения, приведенные на рис. 11.5, что согласно данному методу кодирования соответствует
для этого вентиля получаем значения, приведенные на рис. 11.5, что согласно данному методу кодирования соответствует  . При вычислении
. При вычислении  значения всех разрядов обрабатываются параллельно с помощью соответствующих поразрядных булевых операций.
Напомним, что функции
значения всех разрядов обрабатываются параллельно с помощью соответствующих поразрядных булевых операций.
Напомним, что функции  основных вентилей таковы, что при равенстве компонент входов
основных вентилей таковы, что при равенстве компонент входов 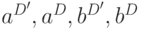 нулю сами функции
нулю сами функции  также равны нулю.
Это дает возможность не вычислять их в том случае, когда соответствующие компоненты входов нулевые. При этом, естественно, надо иметь эффективный способ проверки на равенство нулю компонент входов. Структура модели логического элемента в многозначном алфавите, учитывающей указанные свойства, представлена на рис. 11.6. Заметим также, что внесение константных неисправностей также снижает число логических элементов, имеющих ненулевые компоненты
также равны нулю.
Это дает возможность не вычислять их в том случае, когда соответствующие компоненты входов нулевые. При этом, естественно, надо иметь эффективный способ проверки на равенство нулю компонент входов. Структура модели логического элемента в многозначном алфавите, учитывающей указанные свойства, представлена на рис. 11.6. Заметим также, что внесение константных неисправностей также снижает число логических элементов, имеющих ненулевые компоненты  . Экспериментальные исследования показывают, что в процессе моделирования относительно небольшая часть логических элементов имеет ненулевые компоненты
. Экспериментальные исследования показывают, что в процессе моделирования относительно небольшая часть логических элементов имеет ненулевые компоненты  . Это позволяет проводить моделирование в многозначных алфавитах, в основном, вычисляя две компоненты
. Это позволяет проводить моделирование в многозначных алфавитах, в основном, вычисляя две компоненты  , что существенно повышает скорость моделирования.
, что существенно повышает скорость моделирования.
Внесение неисправностей при моделировании в многозначных алфавитах (включая троичный) обычно производится с помощью специальных масок. Для рассматриваемого метода кодирования это может быть выполнено по следующим формулам:
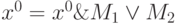 ,
,
 ,
,
 ,
,
 .
Здесь все переменные векторные, их длина равна разрядности машинного слова. Маски
.
Здесь все переменные векторные, их длина равна разрядности машинного слова. Маски  ,
, 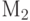 и
и 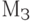 определяют номер разряда в машинном слове и тип вносимой неисправности.
Допустим, что неисправность вносится в
определяют номер разряда в машинном слове и тип вносимой неисправности.
Допустим, что неисправность вносится в  -ом разряде. Тогда маска
-ом разряде. Тогда маска  содержит все единицы (нули) кроме
содержит все единицы (нули) кроме  -го разряда. Значения
-го разряда. Значения  -х разрядов
-х разрядов  ,
, 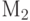 ,
,  определяются типом вносимых неисправностей. Для исправной линии
определяются типом вносимых неисправностей. Для исправной линии 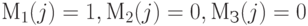 ; для неисправностей const0 -
; для неисправностей const0 -  ; и для неисправностей const1 -
; и для неисправностей const1 -  . Следует отметить, что техника внесения неисправностей с помощью масок достаточно удобна и для моделирования кратных константных и сложных логических неисправностей. Все неисправности, входящие в кратную, должны заноситься в один и тот же разряд.
. Следует отметить, что техника внесения неисправностей с помощью масок достаточно удобна и для моделирования кратных константных и сложных логических неисправностей. Все неисправности, входящие в кратную, должны заноситься в один и тот же разряд.
Ниже представлен псевдокод алгоритма параллельного моделирования неисправностей. Здесь, прежде всего, внешнее описание схемы (текстовое или графическое) транслируется в основную структуру данных - систему связанных таблиц, которая описана в "Машинные модели логических схем и управление процессом моделирования " . Далее выполняется трансляция внешнего описания тестовых воздействий и инициализация табличной модели ДУ. Затем формируется список неисправностей ДУ, подлежащих моделированию. При этом в случае первого сеанса в него заносятся все модельные неисправности данного ДУ с анализом и устранением эквивалентных дефектов. В противном случае список считывается с диска, куда он был записан во время предыдущего сеанса. Далее выполняется основной цикл по неисправностям, в начале которого формируется текущая группа неисправностей, которая затем моделируется на всех тестовых наборах. Функция "смена_набора" вводит следующий тестовый набор и заносит события (изменения сигналов на внешних входах ДУ) в очередь (QJ) на моделирование. Основной является функция "моделирование_набора". В ней реализован событийный алгоритм моделирования в многозначном алфавите.
Существенным ограничением является то, что при параллельном методе моделирования функционирование логических элементов должно быть описано с помощью булевых функций.
Это связано с тем, что основной выигрыш во времени при этом методе получается при выполнении логических операций, которые практически во всех современных ЭВМ реализуются параллельно над всеми разрядами машинных слов. Если элемент описан на функциональном уровне, например, с помощью ЯРП, то нужно каждую сложную функцию (или оператор) описать с помощью булевых функций. Так мы поступали с условным оператором
 ,
заменяя его булевой функцией
,
заменяя его булевой функцией  .
Аналогично можно описать и другие операторы или функции. Сложность модели при этом существенно увеличивается.
.
Аналогично можно описать и другие операторы или функции. Сложность модели при этом существенно увеличивается.
Параллельное_моделирование_неисправностей(схема,тест)
{
Ввод_схемы();
Ввод_теста();
Инициализация_схемы ();
Генерация_сниска_неисправностей();
while(есть неисправности) /* цикл по неисправностям*/
{
Формирование_группы_неисправностей();
while(есть тестовые наборы) /*цикл по тестовым наборам*/
{
Смена_набора(); /* ввод следующего набора */ Внесение_неисправностей_на_внешних_входах(); Моделирование_набора();
Внесение_неисправностей_на_внешних_выходах();
Проверка_обнаружения_неисправностей();
} /* конец цикла по наборам */
Печать_непроверенных_неисправностей();
} /* конец цикла по группам неисправностей */ Печать_полноты_теста(); Запись_непроверенных_неисправностей();
}
Моделирование_набора();
{
Инициализация();
while(есть события)
{
if(есть изменение сигнала)
{
Занесение нового значения в текущий массив;
Запоминание номера контакта первого последователя;
while(циклический список последователей не пуст)
{
Занесение элемента-последователя в очередь QJ;
}
while(очередь QJ не пуста)
{
Выбор элемента-последователя из очереди QJ;
Подготовка данных для моделирования элемента;
if(элемент входит в текущую группу неисправностей)
{
внесение неисправностей на входах элемента;
}
моделирование_элемента();
/* цикл по выходным контактам */
while(есть необработанный выход элемента)
{
if(неисправность контакта входит в текущую группу)
if(новое значение ? старому значению)
{
занесение события в очередь QJ;
} /* конец цикла по выходным контактам */
} /* конец цикла по событиям */
}