|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Последовательное и параллельное моделирование неисправностей
11.1 Задачи моделирования с неисправностями
Моделирование ЦУ с неисправностями является одним из важнейших разделов логического моделирования и используется в системах автоматизированного проектирования и диагностики ДУ при решении следующих задач:
- определение эффективности тестовой последовательности - её полноты и диагностических свойств;
- построение диагностических словарей для поиска неисправностей в логических схемах;
- генерация проверяющих тестов (в качестве инструмента определения эффективности генерируемых наборов);
- анализ поведения схемы и ее свойств с неисправностью.
- Отметим, что наличие неисправности может существенно изменить поведение схемы и привести к следующим последствиям:
- неисправность может вызвать состязания сигналов (отсутствующие в исправной схеме);
- неисправность может вызвать осцилляцию (бесконечное изменение сигналов);
- неисправность может помешать установке схемы с памятью в начальное состояние;
- неисправность может преобразовать комбинационную схему в последовательностную или синхронную - в асинхронную и т.д.
Для решения этих задач программам моделирования неисправных схем требуется следующая информация:
- описание логической схемы;
- описание тестовой входной последовательности;
- модели и список обрабатываемых неисправностей.
Из рассмотренных в предыдущем разделе моделей неисправностей здесь чаще всего используются одиночные константные неисправности. Процесс моделирования неисправных цифровых схем представлен на рис. 11.1.
Здесь неисправности из сокращенного списка вводятся в модель схемы, далее моделируется поведение схемы на входном наборе с последующим анализом. Если неисправность проверяется (дает выходную реакцию, отличную от реакции исправной схемы), то она удаляется из списка и рассматривается следующая. В противном случае подается следующий входной набор. Процесс продолжается до тех пор, пока список неисправностей не будет пуст. Отметим, что анализ неисправных схем может существенно превышать время моделирования исправных схем. Поэтому при моделировании неисправных схем решающим фактором является быстродействие (в то время как для исправных схем важна прежде всего адекватность).
По сравнению с моделированием исправных ДУ при моделировании неисправностей нужно дополнительно выполнить следующие действия:
- Определение множества моделируемых неисправностей;
- Внесение влияния неисправностей;
- Распространение влияния неисправностей;
- Определение проверяемости неисправностей.
Различают условно проверяемые неисправности и проверяемые неисправности. Неисправность считается условно проверяемой, если в результате моделирования на внешнем выходе в неисправной схеме устанавливается неопределенное значение u, а в исправной - определенное значение 0 или 1. Неисправность считается проверяемой, если в результате моделирования хотя бы на одном внешнем выходе исправной и неисправной схем устанавливаются различные определенные значения. Методы моделирования ДУ с неисправностями, в основном, отличаются различной техникой распространения влияния неисправностей.
11.2 Последовательное моделирование
В простейшем случае моделирование неисправностей может быть выполнено любым методом моделирования исправных ДУ путем внесения неисправности в схему в процессе моделирования. При этом, как правило, выполняется моделирование исправной схемы в двоичном алфавите, результаты которого сохраняются для последующего сравнения с выходными реакциями неисправных схем. Далее последовательно выполняется логическое моделирование на тестовой последовательности для каждой неисправной схемы в отдельности. Это производится путем внесения влияния отдельной неисправности в описание схемы и моделирования в двоичном алфавите. В процессе моделирования выходные реакции неисправной схемы после каждого входного набора сравниваются с хранимыми результатами исправной схемы. В случае их расхождения данная неисправность считается проверяемой и моделирование прекращается (для оставшихся входных наборов не выполняется). Этот процесс повторяется последовательно для каждой неисправности из обрабатываемого списка [11.1].
Для исправного устройства моделирование на одном наборе выполняется один раз. В случае неисправного ДУ при наличии  неисправностей в наихудшем случае схема моделируется
неисправностей в наихудшем случае схема моделируется  раз, так как необходимо промоделировать
раз, так как необходимо промоделировать  неисправных и одно исправное ДУ. Соответственно, время моделирования может возрасти в
неисправных и одно исправное ДУ. Соответственно, время моделирования может возрасти в  раз. Это является основным недостатком данного простого метода. К преимуществам метода можно отнести то, что здесь легко моделировать не только константные неисправности, но и неисправности любого другого типа, которые были рассмотрены в предыдущем разделе. При этом проще учесть такие эффекты присутствия неисправности как состязания, осцилляции и т.п., что вызывает определенные проблемы в других методах. Кроме этого, при таком подходе можно локально моделировать неисправности и на электрическом (аналоговом) уровне. Очевидно, что затраты оперативной памяти при этом методе практически не
превышают затрат моделирования исправной схемы. Отметим, что для повышения скорости моделирования при этом методе можно (и удобно) использовать аппаратные ускорители и многопроцессорные системы. В последнее время этот метод все чаще применяется на функциональном уровне, например, для моделирования устройств, описанных на VHDL. Это обуславливается тем, что разработка программ моделирования неисправностей на этом уровне является слишком сложной и чаще проще использовать готовые средства и выполнить моделирование для каждой функциональной неисправности отдельно. Отметим, что некоторые программные средства имеют встроенные средства для внесения функциональных неисправностей.
раз. Это является основным недостатком данного простого метода. К преимуществам метода можно отнести то, что здесь легко моделировать не только константные неисправности, но и неисправности любого другого типа, которые были рассмотрены в предыдущем разделе. При этом проще учесть такие эффекты присутствия неисправности как состязания, осцилляции и т.п., что вызывает определенные проблемы в других методах. Кроме этого, при таком подходе можно локально моделировать неисправности и на электрическом (аналоговом) уровне. Очевидно, что затраты оперативной памяти при этом методе практически не
превышают затрат моделирования исправной схемы. Отметим, что для повышения скорости моделирования при этом методе можно (и удобно) использовать аппаратные ускорители и многопроцессорные системы. В последнее время этот метод все чаще применяется на функциональном уровне, например, для моделирования устройств, описанных на VHDL. Это обуславливается тем, что разработка программ моделирования неисправностей на этом уровне является слишком сложной и чаще проще использовать готовые средства и выполнить моделирование для каждой функциональной неисправности отдельно. Отметим, что некоторые программные средства имеют встроенные средства для внесения функциональных неисправностей.
Однако для повышения эффективности моделирования неисправных схем разработаны специальные методы, которые мы рассмотрим в последующих разделах.
11.3 Параллельное по неисправностям моделирование в двоичном алфавите
В параллельном методе моделирования [11.1,11.4] влияние неисправностей распространяется параллельно для группы схем.
При этом в группу входят одна исправная и множество неисправных схем.
Метод основан на использовании параллелизма при выполнении поразрядных логических операций в процессе моделировании логических элементов.
Если компьютер имеет  -разрядное машинное слово, то обычно одновременно моделируется поведение
-разрядное машинное слово, то обычно одновременно моделируется поведение  схем (одна исправная и
схем (одна исправная и  неисправных). Поэтому все неисправности ДУ разбиваются на группы, содержащие по
неисправных). Поэтому все неисправности ДУ разбиваются на группы, содержащие по  неисправностей и моделирование схемы выполняется
неисправностей и моделирование схемы выполняется ![]N/P-1[](/sites/default/files/tex_cache/f389ed3729a7295eeed6a5307ef73f6e.png) раз, где
раз, где  - количество всех неисправностей. Если схема имеет
- количество всех неисправностей. Если схема имеет  внешних выходов, то число проходов моделирования ограничено снизу следующим выражением
внешних выходов, то число проходов моделирования ограничено снизу следующим выражением ![]N/(P-1)M[](/sites/default/files/tex_cache/43d0fb559463d6dadf661474ea9726d5.png) . Здесь
. Здесь ![] [](/sites/default/files/tex_cache/b803bc2ff18b7c289a5b2502bbd5f390.png) означает
наименьшее сверху целое число.
означает
наименьшее сверху целое число.
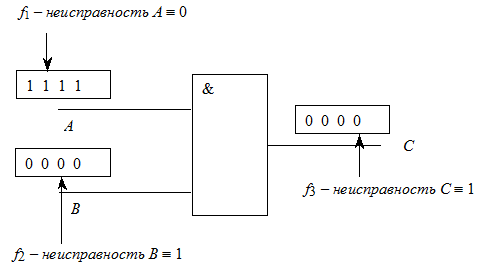
Рассмотрим сначала случай моделирования в двоичном алфавите. При этом каждой линии схемы соответствует одно машинное слово. Внесение влияния неисправностей обычно осуществляется с помощью специальных масок неисправностей. Так, например, неисправность константа 1 вносится путем выполнения операции ИЛИ с маской неисправности, содержащей 1 в разряде, соответствующем этой неисправности. Аналогично неисправность константа 0 вносится с помощью операции И с маской, содержащей 0 в разряде, соответствующем данной неисправности. Рассмотрим 2-входовой вентиль И с константными неисправностями, представленный на рис. 11.2. Допустим, что он является фрагментом некоторой логической схемы. Пусть  ,
,
 и
и  - 4-разрядные (для простоты)машинные слова, хранящие значения сигналов для входов и выхода этого вентиля. Пусть левый разряд представляет исправную схему, остальные биты соответствуют неисправным схемам: второй - неисправности
- 4-разрядные (для простоты)машинные слова, хранящие значения сигналов для входов и выхода этого вентиля. Пусть левый разряд представляет исправную схему, остальные биты соответствуют неисправным схемам: второй - неисправности 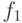 , третий -
, третий -  , четвертый -
, четвертый -  ,
как это показано на рис. 11.2. Тогда внесение неисправности на входах выполняется следующим образом:
,
как это показано на рис. 11.2. Тогда внесение неисправности на входах выполняется следующим образом:
 и
и
 .
.
Далее выполняется собственно логическая операция вентиля  , и затем вносится влияние неисправности на выходе
, и затем вносится влияние неисправности на выходе  .
.
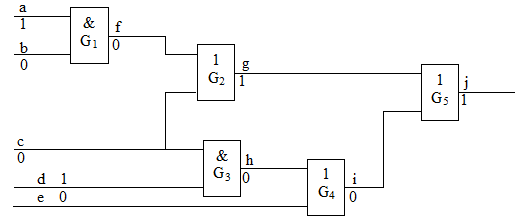
Далее приведем пример параллельного моделирования в двоичном алфавите неисправностей для схемы, представленной на рис. 11.3. При этом будем использовать 16-разрядные машинные слова, соответствующие каждой линии схемы для хранения значений сигналов. Рассматриваются только одиночные константные неисправности (число неисправностей может быть сокращено с помощью методов, рассмотренных в предыдущем разделе, но здесь это не важно).
| Испр. |
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
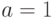
|
1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
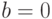
|
0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
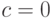
|
0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |

|
1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |

|
0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
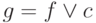
|
0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
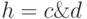
|
0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |

|
0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
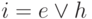
|
0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |

|
0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| + | + | + | + | + | + | + | + |