|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Константные неисправности
Эта схема содержит десять линий и поэтому исходный список состоит из 20 одиночных константных неисправностей. Используя определенные выше отношения эквивалентности неисправностей для вентилей, получаем следующие классы эквивалентных неисправностей:
-
 ;
;
-
 ;
;
-
 ;
;
-
 ;
;
-
 .
.
Поскольку отношения эквивалентности транзитивны и учитывая то, что классы 2, 3 содержат одну и туже неисправность
 , они могут быть объединены в один класс.
, они могут быть объединены в один класс. Кроме отношений эквивалентности между неисправностями имеют место следующие отношения доминирования.
-
 ; поэтому неисправность
; поэтому неисправность  может представлять в списке H 1 и все эквивалентные ей неисправности класса 4.
может представлять в списке H 1 и все эквивалентные ей неисправности класса 4.
-
 ; поэтому неисправность
; поэтому неисправность  может представлять в списке
может представлять в списке  и все эквивалентные ей неисправности класса 5.
и все эквивалентные ей неисправности класса 5.
-
 ; но неисправность
; но неисправность  принадлежит классу 3, который объединен с классом 2. Поэтому любая неисправность из этого класса также доминирует над
принадлежит классу 3, который объединен с классом 2. Поэтому любая неисправность из этого класса также доминирует над  ;
;
-
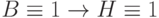 ;
;
-
 ;
;
-
 .
.
Используя эти отношения эквивалентности и доминирования, мы можем сократить список неисправностей до семи:  . Здесь:
. Здесь:  представляет класс 1;
представляет класс 1;  - объединенные классы 2 и 3;
- объединенные классы 2 и 3;  и
и  представляют классы соответственно классы 4 и 5 вследствие отношений доминирования 6 и 7;
неисправности
представляют классы соответственно классы 4 и 5 вследствие отношений доминирования 6 и 7;
неисправности 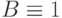 ,
,  ,
,  представляют классы 9, 10, 11 соответственно.
Отметим, что этот сокращенный список не единственен, так как неисправности
представляют классы 9, 10, 11 соответственно.
Отметим, что этот сокращенный список не единственен, так как неисправности  ,
,  могут быть представлены и другими эквивалентными неисправностями из соответствующих классов. Заметим, что сокращенный список содержит неисправности только внешних входов схемы. Это не случайно. Можно показать, что для комбинационных схем без разветвлений достаточно рассматривать только одиночные константные неисправности внешних входов.
могут быть представлены и другими эквивалентными неисправностями из соответствующих классов. Заметим, что сокращенный список содержит неисправности только внешних входов схемы. Это не случайно. Можно показать, что для комбинационных схем без разветвлений достаточно рассматривать только одиночные константные неисправности внешних входов.
Однако для комбинационных схем, содержащих сходящиеся разветвления, этого недостаточно. Необходимо также рассматривать неисправности ветвей разветвлений.
Определение 9.3. Внешние входы и ветви разветвлений называются контрольными точками (checkpoints) комбинационных схем.
Известна следующая теорема контрольных точек [9.2,9.3].
Теорема 9.1. Тестовое множество, проверяющее одиночные константные неисправности контрольных точек комбинационных неизбыточных схем, проверяет любые одиночные константные неисправности этих схем.
Эта теорема позволяет сразу существенно сократить исходное множество рассматриваемых неисправностей. Отметим, что множество одиночных константных неисправностей для контрольных точек также может быть сокращено путем анализа отношений эквивалентности и доминирования. Рассмотрим применение теоремы о контрольных точках на примере схемы рис. 9.4. Эта схема содержит 7 контрольных точек: 5 внешних входа -  ,
,  ,
,  ,
, 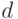 ,
,  и 2 ветви разветвления -
и 2 ветви разветвления - 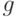 ,
, 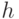 . Поэтому исходное множество неисправностей содержит 14 одиночных неисправностей - s-a-0, s-a-1 для каждой контрольной точки (из всевозможных 24-х).
Дальнейший анализ позволяет это множество еще сократить. Так как неисправности
. Поэтому исходное множество неисправностей содержит 14 одиночных неисправностей - s-a-0, s-a-1 для каждой контрольной точки (из всевозможных 24-х).
Дальнейший анализ позволяет это множество еще сократить. Так как неисправности 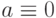 и
и  эквивалентны, то последнюю можно удалить. Аналогично можно удалить неисправность
эквивалентны, то последнюю можно удалить. Аналогично можно удалить неисправность  , которая эквивалентна
, которая эквивалентна  .
Далее неисправность
.
Далее неисправность  эквивалентна
эквивалентна  , которая доминирует над
, которая доминирует над  . Поэтому
. Поэтому  может быть также удалена.
Аналогично
может быть также удалена.
Аналогично  эквивалента
эквивалента  , которая доминирует над
, которая доминирует над  ; поэтому
; поэтому  может быть удалена.
В результате для дальнейшей обработки (генерации тестов или определения полноты теста) остается всего 10 одиночных константных неисправностей (из всевозможных 24-х!):
может быть удалена.
В результате для дальнейшей обработки (генерации тестов или определения полноты теста) остается всего 10 одиночных константных неисправностей (из всевозможных 24-х!):
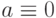 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 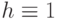 ,
, 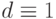 ,
,  .
.
Следует отметить, что приведенная теорема контрольных точек справедлива только для неизбыточных комбинационных схем. В избыточных схемах не все неисправности на избыточных вентилях являются проверяемыми (т.е. для них может быть построен тест). Более того, неисправности на указанных в теореме контрольных точках в избыточных схемах представляют не все одиночные константные неисправности. В таких случаях для этих неисправностей необходимо строить дополнительные тестовые наборы.
Ключевые термины:
Одиночная константная неисправность - фиксирует на линии схемы постоянное значение 0 или 1 независимо от подаваемого на нее сигнала.
Кратная константная неисправность - фиксация постоянных сигналов на нескольких линиях схемы.
Эквивалентность неисправностей - любой тестовый набор, проверяющий одну неисправность, проверяет также и эквивалентную ей неисправность.
Доминирование неисправностей
 - любой тестовый набор, проверяющий
- любой тестовый набор, проверяющий 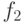 , проверяет также и неисправность
, проверяет также и неисправность  .
.
Конрольные точки - внешние входы и ветви разветвлений комбинационных схем.
Краткие итоги
В лекции рассмотрена базовая модель константных неисправностей, которые позволяют моделировать многие физические дефекты.
В "Константные неисправности" введена модель одиночной константной неисправности, приведены примеры физических дефектов, которые могут быть представлены этой моделью.
"Константные неисправности" посвящен вопросам сокращения множества одиночных константных неисправностей для комбинационных схем. Приведены определения эквивалентности и доминирования неисправностей. Изложены правила локального сокращения множества неисправностей для типовых вентилей. Приведена терема контрольных точек, которая позволяет обрабатывать одиночные константные неисправности только для внешних входов и ветвей разветвления комбинационных схем.
Вопросы и упражнения
- Что такое константная неисправность?
- Чем отличается одиночная константная неисправность от кратной?
- Приведите пример физического дефекта, который можно моделировать константной неисправностью.
- Постройте тест для 3-входового вентиля ИЛИ, проверяющий одиночные константные неисправности.
- Приведите определение и пример эквивалентных неисправностей.
- Покажите, что одиночные константные неисправности
 и
и  схемы рис. 9.5 эквивалентны.
схемы рис. 9.5 эквивалентны.
- Приведите определение и пример доминирования неисправностей.
- Приведите локальные правила сокращения одиночных константных неисправностей.
- Определите для приведенной схемы рис. 9.6 . классы эквивалентности неисправностей.
- Определите для этой схемы отношения доминирования неисправностей.
- Выполните для этой схемы сокращение одиночных константных неисправностей.
- Что такое контрольные точки комбинационной схемы?
- Сформулируйте теорему о контрольных точках.




