|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Константные неисправности
9.1 Модель константных неисправностей
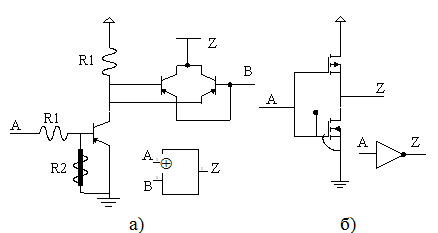
Для определения константных неисправностей используем структурную модель в виде логической схемы. Полагаем, что одиночная константная неисправность (single stack-at fault) действует только на соединение между вентилями (при этом логические элементы функционируют правильно). Каждая линия схемы может иметь два типа этих неисправностей: константа 0 и константа 1 (s-a-0, s-a-1). Итак, константная неисправность фиксирует на данной линии постоянное значение сигнала 0 или 1 (s-a-0, s-a-1), независимо от значения подаваемого на нее сигнала. Часто такие неисправности моделируют замыкания линии схемы на землю (s-a-0) или источник питания (s-a-1). Примеры физических дефектов, представляемых этой моделью, показаны на рис. 9.1. На рис. 9.1 а) показано замыкание входа биполярного транзистора вентиля XOR на землю. Это физический дефект моделируется неисправностью s-a-0. Аналогично на рис. 9.1 б) показан пробой оксида вентиля, реализованного по КМОП технологии, который также моделируется неисправностью s-a-0.
В дальнейшем эта модель будет использоваться для генерации тестов независимо от ее адекватности реальных физических дефектов. Отметим, что для некоторых технологий (например, ТТЛ) адекватность этой модели достаточно высокая, для других (КМОП) ниже. Но в целом, данная модель чрезвычайно полезна в силу своей исключительной простоты и удовлетворительной адекватности, и поэтому используется в качестве базовой для многих методов моделирования неисправностей и генерации тестов[9.1-9.3].
Рассмотрим для примера тест для 3-входового вентиля И (рис. 8.2), проверяющий одиночные константные неисправности.
Очевидно, что тест, представленный табл. 9.1, проверяет все одиночные константные неисправности входов и выхода этого вентиля, поскольку для каждой неисправности в тесте есть входной набор, на котором исправный и неисправный вентиль дают различные выходные реакции. При этом первый входной набор проверяет константные неисправности  ,
,  ,
,  ,
,  . Второй набор проверяет неисправность
. Второй набор проверяет неисправность  , третий -
, третий -  , четвертый -
, четвертый -  .
.
Физический дефект может моделироваться и кратной константной неисправностью, при которой несколько линий принимают постоянное значение 0 или 1 одновременно. Отметим, что число кратных константных неисправностей растет экспоненциально с числом неисправных линий  , составляющих данную неисправность. Для схемы с
, составляющих данную неисправность. Для схемы с  линиями имеется
линиями имеется  одиночных константных неисправностей и
одиночных константных неисправностей и  всевозможных кратных константных неисправностей (включая и одиночные), поскольку каждая линия может быть исправной, либо иметь неисправности s-a-0, s-a-1 (3 возможных события). Очевидно, что для подмножества из
всевозможных кратных константных неисправностей (включая и одиночные), поскольку каждая линия может быть исправной, либо иметь неисправности s-a-0, s-a-1 (3 возможных события). Очевидно, что для подмножества из  фиксированных линий имеется кратных константных неисправностей. Число таких подмножеств определяется
фиксированных линий имеется кратных константных неисправностей. Число таких подмножеств определяется
 .
Поэтому число константных неисправностей с кратностью не более
.
Поэтому число константных неисправностей с кратностью не более  равно
равно
 .
.
9.2 Сокращение списков неисправностей
Поскольку число даже одиночных константных неисправностей достаточно велико для больших схем и время моделирования неисправных устройств и тем более генерации тестов существенно зависит от количества обрабатываемых неисправностей, то исходное множество неисправностей на этапе препроцессорной обработки желательно сократить.
Рассмотрим для простоты комбинационную схему с одним выходом, которая реализует в исправном состоянии булеву функцию
 , а с некоторой
, а с некоторой  -ой неисправностью -
-ой неисправностью -
 . Очевидно, на тестовом проверяющем наборе
. Очевидно, на тестовом проверяющем наборе
 необходимо
необходимо
 .
.
Определение 9.1. Две неисправности
 и
и
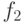 назовем эквивалентными, если любой тестовый набор, проверяющий одну неисправность, проверяет также и другую. Таким образом, их тестовые множества
назовем эквивалентными, если любой тестовый набор, проверяющий одну неисправность, проверяет также и другую. Таким образом, их тестовые множества
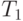 и
и
 идентичны:
идентичны:
 ,
, 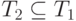 .
.
Для таких неисправностей очевидно
 для произвольного набора
для произвольного набора  .
Рассмотрим множество одиночных константных неисправностей вентиля И, представленного на рис. 8.2.
Очевидно, константные неисправности s-a-0 входов вентиля
.
Рассмотрим множество одиночных константных неисправностей вентиля И, представленного на рис. 8.2.
Очевидно, константные неисправности s-a-0 входов вентиля
 ,
,  ,
,
 эквивалентны неисправности s-a-0 его выхода
эквивалентны неисправности s-a-0 его выхода 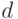 .
Поэтому для последующей обработки можно оставить только одного представителя класса эквивалентных неисправностей, например, s-a-0 входа
.
Поэтому для последующей обработки можно оставить только одного представителя класса эквивалентных неисправностей, например, s-a-0 входа  .
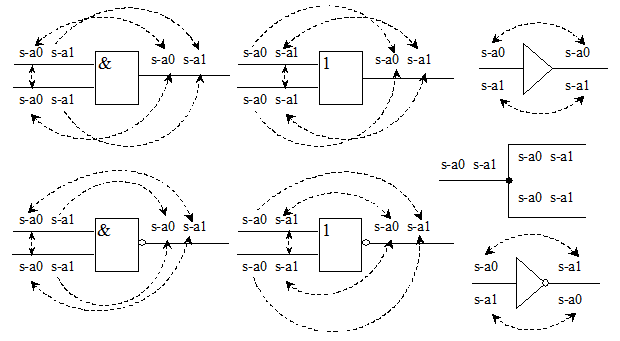
Аналогично константные неисправности s-a-1 входов вентиля ИЛИ эквиваленты неисправности s-a-1 его выхода. Для инвертора неисправность s-a-0 (s-a-1) входа эквивалентна неисправности его выхода s-a-1 (s-a-0)
(рис. 9.2).
.
Аналогично константные неисправности s-a-1 входов вентиля ИЛИ эквиваленты неисправности s-a-1 его выхода. Для инвертора неисправность s-a-0 (s-a-1) входа эквивалентна неисправности его выхода s-a-1 (s-a-0)
(рис. 9.2).
Определение 9.2. Неисправность
 доминирует над неисправностью
доминирует над неисправностью
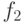 , если тестовое множество последней
, если тестовое множество последней
 является подмножеством тестового множества
является подмножеством тестового множества
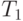 неисправности
неисправности
 , т.е.
, т.е.
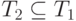 .
.
Таким образом, любой тестовый набор, проверяющий
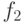 , проверяет также и неисправность
, проверяет также и неисправность  (будем обозначать это отношение
(будем обозначать это отношение
 ). Поэтому для дальнейшей обработки достаточно в список неисправностей включить
). Поэтому для дальнейшей обработки достаточно в список неисправностей включить 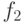 .
.
Возвращаясь назад к примеру вентиля рис. 8.2, находим, что тест для неисправности s-a-1 любого входа элемента И проверяет неисправность s-a-1 его выхода. Здесь неисправность 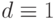 выхода вентиля доминирует над неисправностью s-a-1 любого его входа и поэтому может быть удалена из списка неисправностей этого вентиля. Для определенности оставим в списке неисправность входа
выхода вентиля доминирует над неисправностью s-a-1 любого его входа и поэтому может быть удалена из списка неисправностей этого вентиля. Для определенности оставим в списке неисправность входа 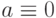 . Таким образом, из восьми возможных одиночных константных неисправностей этого вентиля в списке неисправностей следует оставить только четыре:
. Таким образом, из восьми возможных одиночных константных неисправностей этого вентиля в списке неисправностей следует оставить только четыре:  ,
,
 ,
,
 ,
,
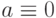 . Таким образом, исходный список неисправностей с помощью приведенных простых правил удалось сократить в два раза. Аналогичные отношения эквивалентности и доминирования имеют место и для других стандартных вентилей. На рис. 9.2 они представлены в наглядной графической форме. При этом неориентированные дуги представляют отношения эквивалентности, а ориентированные - отношения доминирования. Отметим, что для узла разветвления данные отношения отсутствуют.
. Таким образом, исходный список неисправностей с помощью приведенных простых правил удалось сократить в два раза. Аналогичные отношения эквивалентности и доминирования имеют место и для других стандартных вентилей. На рис. 9.2 они представлены в наглядной графической форме. При этом неориентированные дуги представляют отношения эквивалентности, а ориентированные - отношения доминирования. Отметим, что для узла разветвления данные отношения отсутствуют.
В общем виде, локальное сокращение списка неисправностей для вентиля выполняется согласно следующим правилам [9.1,9.2]:
- Для вентиля с
 входами из всех
входами из всех  возможных неисправностей необходимо рассматривать
возможных неисправностей необходимо рассматривать  одиночных константных неисправностей.
одиночных константных неисправностей.
- При этом удаляются обе неисправности s-a-0, s-a-1 выхода любого вентиля и оставляются одиночные константные неисправности типа s-a-0 (s-a-1) для каждого входа вентиля ИЛИ, НЕ-ИЛИ (И, НЕ-И) и одна неисправность любого входа противоположного типа s-a-1 для ИЛИ, НЕ-ИЛИ (s-a-0 для И, НЕ-И).
- Одиночные константные неисправности выхода вентиля НЕ и неинвертирующего буфера удаляются, а входа - оставляются.
- Для узла разветвления сокращение неисправностей не производится, так как между ними нет отношения эквивалентности и доминирования.
Далее, используя отношения эквивалентности и доминирования неисправностей для отдельных вентилей, мы можем распространить его на неисправности всей схемы.
Рассмотрим в качестве примера комбинационную схему, не содержащую разветвлений, которая представлена на рис. 9.3.