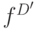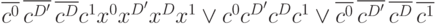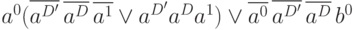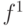|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Система многозначных алфавитов и функций
Моделирование шинных структур
Моделирование схем, содержащих тристабильные элементы, представляет особый интерес. Корректное моделирование таких схем даже в статике требует 3-значного алфавита  , где
, где  -представляет состояние высокого импеданса. При моделировании переходных процессов используют, как минимум, 4-значный алфавит
-представляет состояние высокого импеданса. При моделировании переходных процессов используют, как минимум, 4-значный алфавит 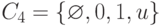 , где
, где  интерпретируется как неопределенное значение (
интерпретируется как неопределенное значение ( или
или  или
или  ). Наибольшие трудности вызывает, как правило, моделирование шинных структур, одна из которых представлена на рис.7.3.
). Наибольшие трудности вызывает, как правило, моделирование шинных структур, одна из которых представлена на рис.7.3.
При этом выходы цифровых устройств подключаются к шине обычно через тристабильные элементы, которые при управляющем сигнале  пропускают информационный сигнал (
пропускают информационный сигнал ( ), а при
), а при  отключают устройство от шины (
отключают устройство от шины ( ). В табл.7.10 представлена модель такого элемента в алфавите
). В табл.7.10 представлена модель такого элемента в алфавите  , которая часто используется на практике
[
7.5
]
.
, которая часто используется на практике
[
7.5
]
.
Поставим в соответствие символу  в принятом нами методе кодирования код-
в принятом нами методе кодирования код- Тогда 4-значный алфавит
Тогда 4-значный алфавит  образует следующее подмножество
образует следующее подмножество

На основании табл.7.10 с учетом принятого метода кодирования получены функции  для тристабильного элемента, которые приведены в табл.7.12.
для тристабильного элемента, которые приведены в табл.7.12.
Как уже отмечалось, выходы тристабильных элементов обычно подключаются к шине, модель которой в алфавите  представлена в табл.7.11. Если все устройства отключены, то согласно этой таблице шина находится в состоянии высокого импеданса. Это не всегда соответствует действительности, так как при некоторых технологиях в таком случае шина сохраняет предыдущее значение. То есть в этом случае значение
представлена в табл.7.11. Если все устройства отключены, то согласно этой таблице шина находится в состоянии высокого импеданса. Это не всегда соответствует действительности, так как при некоторых технологиях в таком случае шина сохраняет предыдущее значение. То есть в этом случае значение  на шине скорее является признаком сохранения предыдущего значения. На основании табл.7.11 для принятого метода кодирования получены функции
на шине скорее является признаком сохранения предыдущего значения. На основании табл.7.11 для принятого метода кодирования получены функции  , которые представлены в табл.7.12.
, которые представлены в табл.7.12.
Моделирование МОП-схем требует введения специальных приоритетов ("сил"). При этом с линией схемы обычно связывается два параметра  , где
, где  соответствует напряжению, а "сила"
соответствует напряжению, а "сила"  соответствует току или заряду [53]. Введение "силы" позволяет корректно моделировать на логическом уровне специальные элементы (типа "сборка" и т.п.), которые традиционно моделировались на уровне электронных схем. Следуя
[
2.2
]
, в этом случае алфавит моделирования можно представить в виде
соответствует току или заряду [53]. Введение "силы" позволяет корректно моделировать на логическом уровне специальные элементы (типа "сборка" и т.п.), которые традиционно моделировались на уровне электронных схем. Следуя
[
2.2
]
, в этом случае алфавит моделирования можно представить в виде  , где
, где  и
и 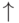 представляет операцию конкатенации, при которой элементы в алфавите
представляет операцию конкатенации, при которой элементы в алфавите  и
и  "стягиваются" в
"стягиваются" в  На рис.7.2 д представлены диаграммы Хассе
На рис.7.2 д представлены диаграммы Хассе  для
для  В настоящее время наиболее распространенными являются алфавиты типа
В настоящее время наиболее распространенными являются алфавиты типа  При этом высший приоритет (
При этом высший приоритет ( ) соответствует линиям схемы, связанным с питанием или землей. Выходам логических элементов обычно присваивается следующий приоритет (
) соответствует линиям схемы, связанным с питанием или землей. Выходам логических элементов обычно присваивается следующий приоритет ( ). И самый низкий приоритет (
). И самый низкий приоритет ( ) имеют элементы, у которых сигналы хранятся на емкостях. Как правило, наибольшие трудности вызывает моделирование специальных элементов типа "сборка". Математически моделирование "сборки" сводится к операции
) имеют элементы, у которых сигналы хранятся на емкостях. Как правило, наибольшие трудности вызывает моделирование специальных элементов типа "сборка". Математически моделирование "сборки" сводится к операции  - нахождению наименьшей верхней грани в
- нахождению наименьшей верхней грани в  . Например,
. Например, 
Функции  используются при моделировании логических элементов для вычисления параметра
используются при моделировании логических элементов для вычисления параметра  "Сила"
"Сила"  определяется типом элемента и применяемой технологией. Существуют различные модификации многозначных алфавитов, являющихся подмножествами
определяется типом элемента и применяемой технологией. Существуют различные модификации многозначных алфавитов, являющихся подмножествами  Интересным и важным для практики представляется 9-значный алфавит. Этот алфавит получается из
Интересным и важным для практики представляется 9-значный алфавит. Этот алфавит получается из  удалением элемента
удалением элемента  и имеет структуру несколько отличную от
и имеет структуру несколько отличную от  , которая обусловлена технологией производства рассматриваемых схем.
, которая обусловлена технологией производства рассматриваемых схем.
Представленные выше модели тристабильного элемента и шины используют четыре компоненты  Но при моделировании в алфавитах
Но при моделировании в алфавитах 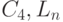 достаточно использовать только две компоненты и не все термы
достаточно использовать только две компоненты и не все термы  При этом модели тристабильного элемента и шины существенно упрощаются. Для тристабильного элемента в этом случае получаем
При этом модели тристабильного элемента и шины существенно упрощаются. Для тристабильного элемента в этом случае получаем  и
и  Аналогично для шины имеем
Аналогично для шины имеем 
Разработанная система многозначных функций является универсальной математической моделью, которая позволяет решать широкий класс задач диагностики, включая моделирование исправных и неисправных цифровых устройств и генерацию проверяющих тестов в основных многозначных алфавитах, которые будут рассмотрены в последующих разделах. Применение разработанных моделей на функциональном уровне увеличивает эффективность программ моделирования и генерации тестов.
Ключевые термины:
Многозначный алфавит – множество символов, отражающих распределение сигналов в схеме.
Многозначная функция – определяется на произвольном  -значном алфавите
-значном алфавите 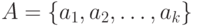 как отображение
как отображение  , где
, где  –число аргументов функции.
–число аргументов функции.
Краткие итоги
Данная лекция посвящена проблемам моделирования логических схем в многозначных алфавитах.
В разделе 7.1 на основе двоичного алфавита вводится универсальный 16-значный алфавит, который включает в себя основные многозначные алфавиты, используемые в логическом моделировании и генерации тестов. Рассмотрен два основных способа построения алфавитов большей значности :
- как подмножество некоторого декартова произведения исходного алфавита;
- как множество подмножеств исходного алфавита.
В разделе 7.2 рассмотрено построение многозначных функций на базе:
В разделе 7.3 показано, что основные многозначные алфавиты, используемые в логическом моделировании и генерации тестов, являются подмножествами универсального 16-значного алфавита.
Раздел 7.4 посвящен исследованию алгебраической структуры основных многозначных алфавитов.
В разделе 7.5 описывается моделирование шинных структур с использованием4-значного алфавита.
Вопросы и упражнения
- Где и почему используются многозначные алфавиты ?
- Какие два основных способа построения алфавитов большей значности из исходного алфавита вы знаете?
- Опишите физический смысл символов универсального 16-значного алфавита.
- Зачем нужны многозначные функции?
- Приведите два основных способа описания многозначных функций.
- Опишите табличное представление многозначной функции.
- Опишите компонентное представление многозначной функции.
- Каким образом получаются основные многозначные алфавиты, используемые при моделировании и генерации тестов, из универсального 16-значного алфавита?
- Опишите алгебраическую структуру основных многозначных алфавитов.
- Какой алфавит используется для моделирования шинных структур?
- Опишите табличные многозначные модели элементов шинных структур.
- Опишите компонентные модели элементов шинных структур.