|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Система многозначных алфавитов и функций
Основные многозначные алфавиты как подмножества универсального 16-значного алфавита
Наиболее широко применяемый на практике алфавит 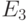 образует следующее подмножество алфавита
образует следующее подмножество алфавита  Рассмотрим пример вычисления функции
Рассмотрим пример вычисления функции  в троичном алфавите, используя характеристические функции, приведенные в Табл.7.5.
в троичном алфавите, используя характеристические функции, приведенные в Табл.7.5.
Пусть  , и
, и  , тогда получаем
, тогда получаем
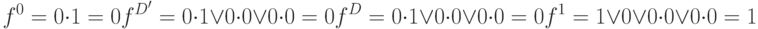
Таким образом, согласно кодированию алфавита 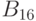 (Табл.7.1) код
(Табл.7.1) код  определяет значение
определяет значение 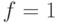 , что соответствует таблице истинности функции
, что соответствует таблице истинности функции  в троичном алфавите.
в троичном алфавите.
Алфавит 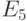 , являющийся расширением алфавита E3, определяется следующим подмножеством 16-значного алфавита:
, являющийся расширением алфавита E3, определяется следующим подмножеством 16-значного алфавита:
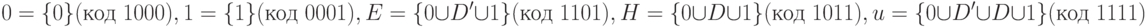
Рассмотрим пример вычисления функции  в 5-значном алфавите, используя характеристические функции, приведенные в Табл.7.5.
в 5-значном алфавите, используя характеристические функции, приведенные в Табл.7.5.
Пусть  , и
, и  , тогда получаем
, тогда получаем
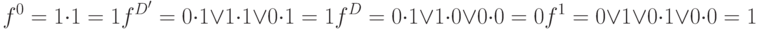
То есть, согласно кодированию алфавита 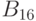 код
код  определяет значение
определяет значение  что соответствует таблице истинности функции
что соответствует таблице истинности функции  в 5-значном алфавите.
в 5-значном алфавите.
На рис.7.2 представлена алгебраическая структура алфавитов 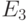 и
и  В силу построения рассмотренные алфавиты являются частично упорядоченными подмножествами и образуют структуры типа верхняя полурешетка
В силу построения рассмотренные алфавиты являются частично упорядоченными подмножествами и образуют структуры типа верхняя полурешетка
| Элементы | Интерпретация |
|---|---|
 |
Статический 
|
 |
Статическая 
|
 |
Переход 
|
 |
Переход 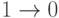
|
 |
Статическое  -состязание -состязание |
 |
Статическое  -состязание -состязание |
| Элементы | Интерпретация |
|---|---|
 |
Статический 
|
 |
Статическая 
|
 |
Переход 
|
 |
Переход 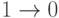
|
 |
Статическое  -состязание -состязание |
 |
Статическое  -состязание -состязание |
 |
Динамическое  -состязание -состязание |
 |
Динамическое  -состязание -состязание |
Отметим, что 6-значный и 8-значный алфавиты  и
и  соответственно, используемые в методах анализа состязаний сигналов также могут быть получены из алфавита
соответственно, используемые в методах анализа состязаний сигналов также могут быть получены из алфавита 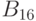 , так как определяются следующими подмножествами:
, так как определяются следующими подмножествами:  При этом, как было показано в разделе 2.9.2, моделирование с анализом на состязания выполняется на трех наборах: текущем основном в алфавите
При этом, как было показано в разделе 2.9.2, моделирование с анализом на состязания выполняется на трех наборах: текущем основном в алфавите  , на промежуточном наборе: при использовании
, на промежуточном наборе: при использовании  - в алфавите
- в алфавите 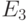 (при использовании
(при использовании  - в алфавите
- в алфавите 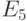 ) следующем основном наборе в алфавите
) следующем основном наборе в алфавите  Такой способ моделирования с использованием трех наборов соответствует математической структуре алфавитов
Такой способ моделирования с использованием трех наборов соответствует математической структуре алфавитов  и
и  Результаты моделирования интерпретируются в соответствии с таблицами 7.8 и 7.9 соответственно. Отметим, что алфавит
Результаты моделирования интерпретируются в соответствии с таблицами 7.8 и 7.9 соответственно. Отметим, что алфавит  позволяет обнаруживать динамические состязания. В алгоритмах анализа состязаний иногда используется также алфавит
позволяет обнаруживать динамические состязания. В алгоритмах анализа состязаний иногда используется также алфавит  , содержащий все элементы алфавита
, содержащий все элементы алфавита  и элемент
и элемент  , соответствующий неопределенному состоянию.
, соответствующий неопределенному состоянию.
Алфавит  , наиболее широко применяемый в методах генерации тестов (он будет дальше использоваться в лекции является подмножеством 16-значного алфавита:
, наиболее широко применяемый в методах генерации тестов (он будет дальше использоваться в лекции является подмножеством 16-значного алфавита:
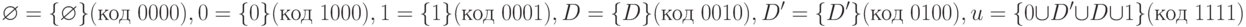
Рассмотрим пример вычисления функции  в 6-значном алфавите, используя характеристические функции, приведенные в Табл.7.5. Пусть
в 6-значном алфавите, используя характеристические функции, приведенные в Табл.7.5. Пусть  , и
, и  , тогда получаем
, тогда получаем
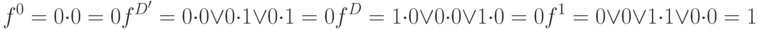
То есть, согласно кодированию алфавита 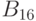 (Табл.7.1) код
(Табл.7.1) код  определяет значение
определяет значение 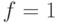 , что соответствует таблице истинности функции
, что соответствует таблице истинности функции  в алфавите
в алфавите 
Широкое применение в методах генерации тестов находит также алфавит  , являющийся подмножеством 16-значного алфавита. Он определяется следующим его подмножеством:
, являющийся подмножеством 16-значного алфавита. Он определяется следующим его подмножеством:
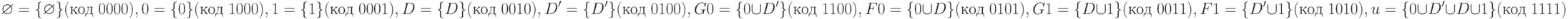
Рассмотрим пример вычисления функции  в 10-значном алфавите, используя характеристические функции, приведенные в Табл.7.5. Пусть
в 10-значном алфавите, используя характеристические функции, приведенные в Табл.7.5. Пусть  , и
, и  , тогда получаем
, тогда получаем

Тогда, согласно кодированию алфавита 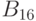 (Табл.7.1), код
(Табл.7.1), код  определяет значение
определяет значение  , что соответствует таблице истинности функции
, что соответствует таблице истинности функции  в алфавите
в алфавите  В генерации тестов используется также и 12-значный
В генерации тестов используется также и 12-значный  алфавит, также являющиеся расширением алфавита
алфавит, также являющиеся расширением алфавита 
Из выше сказанного можно сделать заключение, что при методе кодирования, используемом в алфавите  , описание поведения многозначных функций с помощью упорядоченного множества характеристических функций
, описание поведения многозначных функций с помощью упорядоченного множества характеристических функций  может быть использовано в методах генерации тестов и моделирования логических схем, базирующихся на применении основных многозначных алфавитов. С этой точки зрения описанная 16-значная логика
может быть использовано в методах генерации тестов и моделирования логических схем, базирующихся на применении основных многозначных алфавитов. С этой точки зрения описанная 16-значная логика  является универсальной математической моделью для методов генерации тестов и моделирования.
является универсальной математической моделью для методов генерации тестов и моделирования.
Алгебраическая структура многозначных алфавитов
Показано, что рассмотренный 16-значный алфавит 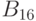 образует булеву алгебру, представленную на Рис.7.1. Используемый метод построения позволяет утверждать, что основные многозначные алфавиты, применяемые в методах генерации проверяющих тестов и моделирования ДУ, являются частично упорядоченными подмножествами
образует булеву алгебру, представленную на Рис.7.1. Используемый метод построения позволяет утверждать, что основные многозначные алфавиты, применяемые в методах генерации проверяющих тестов и моделирования ДУ, являются частично упорядоченными подмножествами  Так, например, алфавиты
Так, например, алфавиты 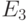 и
и 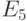 образуют структуры типа верхняя полурешетка, которые не содержат наименьший элемент. Эти структуры представлены на рис.7.2а и рис.7.2б. Если к алфавиту
образуют структуры типа верхняя полурешетка, которые не содержат наименьший элемент. Эти структуры представлены на рис.7.2а и рис.7.2б. Если к алфавиту 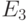 добавить наименьший элемент
добавить наименьший элемент  , то получим алфавит
, то получим алфавит  , также представленный на рис.7.2в, который используется при моделировании шинных структур. Знание алгебраической структуры основных многозначных алфавитов позволяет строить с помощью алгебраических операций новые алфавиты, необходимые при моделировании или генерации тестов схем, выполненных по какой либо новой технологии. Например, на рис.7.2г, рис.7.2д представлены алфавиты
, также представленный на рис.7.2в, который используется при моделировании шинных структур. Знание алгебраической структуры основных многозначных алфавитов позволяет строить с помощью алгебраических операций новые алфавиты, необходимые при моделировании или генерации тестов схем, выполненных по какой либо новой технологии. Например, на рис.7.2г, рис.7.2д представлены алфавиты 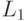 и
и  , которые получены из алфавита
, которые получены из алфавита  и широко используются при моделировании шинных структур.
и широко используются при моделировании шинных структур.


