|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Анализ состязаний
Анализ состязаний по методу Эйхельбергера
На практике большое распространение получили системы логического моделирования в троичном алфавите 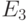 . Моделирование в троичном алфавите последовательностных схем в простейшем случае используется для проверки, является ли данная входная последовательность установочной, т. е. переводит ли она схему из неопределенного начального состояния в некоторое определенное. Поскольку перед началом моделирования схема находится в произвольном состоянии, то сигнал на каждой линии может иметь значение как
. Моделирование в троичном алфавите последовательностных схем в простейшем случае используется для проверки, является ли данная входная последовательность установочной, т. е. переводит ли она схему из неопределенного начального состояния в некоторое определенное. Поскольку перед началом моделирования схема находится в произвольном состоянии, то сигнал на каждой линии может иметь значение как  , так и
, так и  . Поэтому перед началом моделирования всем линиям схемы присваивается неопределенное значение
. Поэтому перед началом моделирования всем линиям схемы присваивается неопределенное значение  . Далее выполняется моделирование на последовательности входных наборов (имеющих двоичные значения
. Далее выполняется моделирование на последовательности входных наборов (имеющих двоичные значения  ) с помощью одного из рассмотренных алгоритмов. При этом используются троичные модели логических элементов. Если по окончании моделирования все линии схемы принимают определенные значения (
) с помощью одного из рассмотренных алгоритмов. При этом используются троичные модели логических элементов. Если по окончании моделирования все линии схемы принимают определенные значения ( ), то входная последовательность является установочной (в терминах теории экспериментов с автоматами – синхронизирующей последовательностью см.
"Структурное построение тестов для устройств с памятью"
). На практике часто надо получить определенные значения не на всех линиях, а только на некоторых. Очевидно, описанный метод позволяет проверить, является ли входная последовательность установочной для некоторого подмножества линий.
), то входная последовательность является установочной (в терминах теории экспериментов с автоматами – синхронизирующей последовательностью см.
"Структурное построение тестов для устройств с памятью"
). На практике часто надо получить определенные значения не на всех линиях, а только на некоторых. Очевидно, описанный метод позволяет проверить, является ли входная последовательность установочной для некоторого подмножества линий.
Моделирование в троичном алфавите 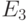 с успехом используется и для анализа состязаний сигналов, которые могут вызвать неправильное функционирование ДУ (перевести его в непредусмотренное состояние). Поэтому при проектировании ДУ стараются не допустить состязаний на подмножестве входных рабочих последовательностей (применяют противогоночное кодирование, вводят специальные задержки и т. д.). Но проверяющие тесты строятся не только на рабочих наборах. Поэтому даже для "хорошо" спроектированных ДУ (без состязаний на рабочих воздействиях) отсутствие анализа тестов на состязания может при тестировании привести к пропуску неисправности, либо, наоборот, к ее ложному обнаружению.
с успехом используется и для анализа состязаний сигналов, которые могут вызвать неправильное функционирование ДУ (перевести его в непредусмотренное состояние). Поэтому при проектировании ДУ стараются не допустить состязаний на подмножестве входных рабочих последовательностей (применяют противогоночное кодирование, вводят специальные задержки и т. д.). Но проверяющие тесты строятся не только на рабочих наборах. Поэтому даже для "хорошо" спроектированных ДУ (без состязаний на рабочих воздействиях) отсутствие анализа тестов на состязания может при тестировании привести к пропуску неисправности, либо, наоборот, к ее ложному обнаружению.
При синхронном моделировании в двоичном алфавите нельзя обнаружить состязания. При асинхронном моделировании в этом алфавите их можно обнаруживать только в некоторых случаях (например, при возникновении режима генерации).
Для анализа состязаний широкое распространение получил метод Эйхельбергера, который основан на предположении, что соотношение задержек в элементах и линиях связей произвольно. Символ  при этом означает не только неизвестный сигнал, но и смену сигналов
при этом означает не только неизвестный сигнал, но и смену сигналов 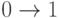 или
или 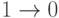 .
.
В методе Эйхельбергера моделирование входного набора  выполняется в два этапа. Сначала формируется промежуточный набор
выполняется в два этапа. Сначала формируется промежуточный набор  , в котором всем входным переменным, изменившим значение по сравнению с набором
, в котором всем входным переменным, изменившим значение по сравнению с набором  , присваивается неопределенное значение
, присваивается неопределенное значение  (остальные значения остаются неизменными и равны
(остальные значения остаются неизменными и равны  или
или  ) так, как это показано в табл.6.1 для схемы рис. 2.5 . Затем выполняется моделирование в троичном алфавите на промежуточном наборе
) так, как это показано в табл.6.1 для схемы рис. 2.5 . Затем выполняется моделирование в троичном алфавите на промежуточном наборе  (при этом, естественно, используются троичные модели логических элементов). На этом этапе моделируется переходный процесс, во время которого всем линиям, которые существенно зависят от изменившихся входов на данном наборе, присваиваются неопределенные значения
(при этом, естественно, используются троичные модели логических элементов). На этом этапе моделируется переходный процесс, во время которого всем линиям, которые существенно зависят от изменившихся входов на данном наборе, присваиваются неопределенные значения  . При этом неопределенные значения распространяются от внешних входов к выходам и переменным состояния до тех пор, пока значения сигналов не стабилизируются. Свойства троичных функций таковы, что значение сигнала на каждом элементе либо остается неизменным (
. При этом неопределенные значения распространяются от внешних входов к выходам и переменным состояния до тех пор, пока значения сигналов не стабилизируются. Свойства троичных функций таковы, что значение сигнала на каждом элементе либо остается неизменным ( ), либо изменяется (с
), либо изменяется (с  или
или  на
на  ). Поэтому процедура имеет линейную сложность (пропорционально числу элементов
). Поэтому процедура имеет линейную сложность (пропорционально числу элементов  в ДУ).
в ДУ).
На втором этапе ДУ моделируется на основном наборе  (значения всех входов которого двоичные). При этом от входов к выходам происходит "снятие" неопределенности. Вследствие свойства троичных функций на каждом логическом элементе сигнал либо остается постоянным, либо изменяется с
(значения всех входов которого двоичные). При этом от входов к выходам происходит "снятие" неопределенности. Вследствие свойства троичных функций на каждом логическом элементе сигнал либо остается постоянным, либо изменяется с  на
на  или
или  . Поэтому на втором этапе сложность процедуры также линейна.
. Поэтому на втором этапе сложность процедуры также линейна.
| Набор | 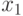 |
 |
 |
 |
 |
 |
 |
 |
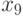 |
|---|---|---|---|---|---|---|---|---|---|
| u | u | u | u | u | u | u | u | u | |
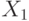 |
1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
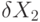 |
u | 1 | 0 | u | 1 | u | u | u | U |
 |
0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
 |
u | 1 | 0 | 1 | 1 | u | 0 | u | 1 |
 |
1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
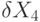 |
1 | 1 | u | 1 | u | u | u | u | u |
 |
1 | 1 | 1 | 1 | 0 | 1 | 1 | u | u |
Если по окончании второго этапа на некоторых линиях ДУ остались неопределенные значения  , то это свидетельствует о возможности опасных состязаний на этих линиях. На линиях, получивших после второго этапа определенные значения, состязания в схеме на данном наборе невозможны. Если все линии ДУ получили определенные значения, состязания в схеме на моделируемом переходе между двумя наборами заведомо отсутствуют.
, то это свидетельствует о возможности опасных состязаний на этих линиях. На линиях, получивших после второго этапа определенные значения, состязания в схеме на данном наборе невозможны. Если все линии ДУ получили определенные значения, состязания в схеме на моделируемом переходе между двумя наборами заведомо отсутствуют.
Отметим, что в данном методе анализ выполняется чисто логическими средствами без задания каких-либо значений задержек элементов. Метод основан на анализе логической зависимости элементов схемы от изменившихся входов. Простота метода и линейная сложность обусловили его широкое применение на практике. Пример моделирования в троичном алфавите методом Эйхельбергера приведен для схемы на рис.6.5 .
Результаты моделирования, представленные в табл. 6.1 , показывают, что набор 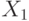 является установочным, на переходах между наборами
является установочным, на переходах между наборами 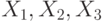 состязания отсутствуют, а при переходе с
состязания отсутствуют, а при переходе с  на
на  возникают опасные состязания. Доказано, что моделирование методом Эйхельбергера на обоих этапах сходится за конечное число итераций. Поэтому при реализации единственным критерием окончания моделирования на наборе (промежуточном и основном) является совпадение результатов двух соседних итераций. При этом результаты не зависят от порядка обработки элементов. Отметим, что троичное моделирование в данном методе может выполняться с помощью простейшей (и быстродействующей) модели элементов – нулевой задержки.
возникают опасные состязания. Доказано, что моделирование методом Эйхельбергера на обоих этапах сходится за конечное число итераций. Поэтому при реализации единственным критерием окончания моделирования на наборе (промежуточном и основном) является совпадение результатов двух соседних итераций. При этом результаты не зависят от порядка обработки элементов. Отметим, что троичное моделирование в данном методе может выполняться с помощью простейшей (и быстродействующей) модели элементов – нулевой задержки.
Троичное моделирование по методу Эйхельбергера позволяет обнаружить любые опасные состязания, которые могут быть в ДУ на данной входной последовательности. Однако этот метод имеет существенный недостаток — он может показывать наличие состязаний в тех случаях, когда их нет в реальном устройстве. Это обусловлено принятым допущением о произвольном соотношении задержек элементов и линий связи. В действительности обычно задержки в линиях связи существенно меньше задержек логических элементов. Соотношение между задержками элементов также не всегда произвольно. Ложные состязания метод Эйхельбергера может показывать в схемах, содержащих сходящиеся разветвления, искусственные линии задержки из цепочек элементов и, особенно, в счетных структурах, где любое переключение счетного входа приводит к обнаружению состязаний.
В какой-то мере этот недостаток устранен в методе моделирования, получившем название  -троичного и являющегося модификацией предыдущего. Суть метода заключается в том, что моделирование на промежуточном наборе ограничивается сверху некоторым числом итераций
-троичного и являющегося модификацией предыдущего. Суть метода заключается в том, что моделирование на промежуточном наборе ограничивается сверху некоторым числом итераций  . Параметр
. Параметр  задается заранее и косвенно отражает степень разброса задержек элементов в схеме. При этом распространение неопределенных значений
задается заранее и косвенно отражает степень разброса задержек элементов в схеме. При этом распространение неопределенных значений  искусственно прекращается, не дожидаясь, пока процесс сойдется. При
искусственно прекращается, не дожидаясь, пока процесс сойдется. При  -троичном моделировании используется модель единичной задержки. Сходимость этого метода не гарантирована, поэтому после выполнения максимального числа итераций всем линиям, на которых сигналы не установились, присваивается неопределенное значение.
-троичном моделировании используется модель единичной задержки. Сходимость этого метода не гарантирована, поэтому после выполнения максимального числа итераций всем линиям, на которых сигналы не установились, присваивается неопределенное значение.
Отметим еще раз, что в рассмотренном методе в процессе моделирования используются троичные модели логических элементов, кратко представленные в "Модели логических элементов" и более детально описанные в следующей "Система многозначных алфавитов и функций" . Троичное моделирование часто выполняется не только на логическом уровне, но и на уровне регистровых передач. При этом используются троичные модели операторов ЯРП, которые разработаны и представлены в [ 1.2 ] .
Ключевые термины:
Функциональное состязание – определяется на паре двоичных наборов свойствами булевой функции и заключается в появлении на выходе схемы кратковременного импульса.
Логическое состязание - определяется на паре двоичных наборов свойствами логической схемы и заключается в появлении на выходе схемы кратковременного импульса.
Троичное моделирование – логическое моделирование в троичном алфавите  .
.
Краткие итоги
Лекция посвящена вопросам анализа состязаний сигналов в логических схемах.
В разделе 6.1 описано явление состязания сигналов. В разделе 6.1.1 рассмотрен и приведен на карте Карно пример функционального состязания . и схема,. Раздел 6.1.2 посвящен логическим состязаний .
В разделе 6.2 изложен метод Эйхельбергера анализа состязаний, который основан на троичном моделировании и имеет линейную сложность.
Вопросы и упражнения
- Опишите явление состязаний сигнала.
- Что такое функциональные состязания сигналов?
- Чем отличаются логические состязания сигналов от функциональных ?
- Чем опасно явление состязаний сигналов?
- Как вы думаете: для каких схем – комбинационных или последовательностных, более опасно это явление?
- Что лежит в основе анализа состязаний методом Эйхельбергера?
- Какие этапы присутствуют в этом методе?
- Что определяется на первом этапе анализа состязаний?
- Что определяется на втором этапе состязаний?
- Какую сложность (от числа элементов) имеет метод Эйхельбергера?
- Какие недостатки имеет этот метод?

