|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Модели логических элементов
Модели задержек логических элементов
При логическом моделировании важнейшим фактором, определяющим достоверность модели по отношению к реальной схеме, является учет задержек распространения сигналов через элементы. В этом разделе мы рассмотрим способы представления задержек, их особенности и ограничения.
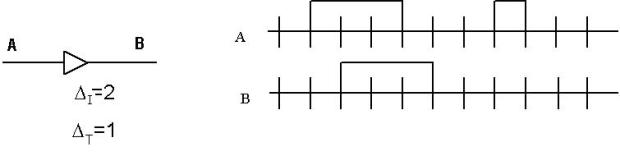
Простейшей формой модельной задержки является модель транспортной задержки , при которой логический элемент рассматривается состоящим из двух каскадов, как это показано на рис.4.3. При этом в первом каскаде реализуется его логическая функция (предполагается мгновенное распространение сигнала от входа до выхода), а второй каскад моделирует задержку распространения сигнала от входов элемента до его выхода.
На практике применяются различные модели транспортной задержки. При моделировании без учета задержек элементов, в частности, когда время задержки принимается равным нулю, используют модель с нулевыми задержками. Модель с нулевыми задержками применяется только для моделирования комбинационных и синхронных последовательностных схем.
Модель, в которой времена задержек всех логических элементов считаются одинаковыми, носит название модели с единой (или единичной) задержкой. Благодаря тому, что элементам присвоены задержки, появляется возможность обрабатывать асинхронные схемы с обратными связями и проводить хотя бы приближенный анализ временных соотношений в схеме. В общем случае, однако, следует учитывать то, что различные типы логических элементов обладают разными задержками. Поэтому более адекватной является модель с номинальными задержками, при которой каждому логическому элементу присваивается свое целочисленное значение задержки, измеряемое в единицах модельного времени. Для того чтобы осуществить соответствующее этому случаю моделирование, в качестве базовой единицы модельного времени обычно используют наибольший общий делитель времен задержек  элементов и присваивают значения задержек в соответствии с их кратностью.
элементов и присваивают значения задержек в соответствии с их кратностью.
Пример. Пусть для схемы, показанной на рис. 4.4 , выполняется моделирование с использованием модели с
единичной задержкой. На рис.4.5а) представлены результаты логического моделирования с использованием модели единичных задержек в виде
временных диаграмм сигналов на линиях схемы. На рис.4.5б) показаны временные диаграммы для той же схемы, но с использованием модели
номинальных задержек, где время задержки элементов  составляет
составляет 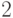 единицы, а для остальных элементов –
единицы, а для остальных элементов –  (здесь одно деление
соответствует единице модельного времени).
(здесь одно деление
соответствует единице модельного времени).
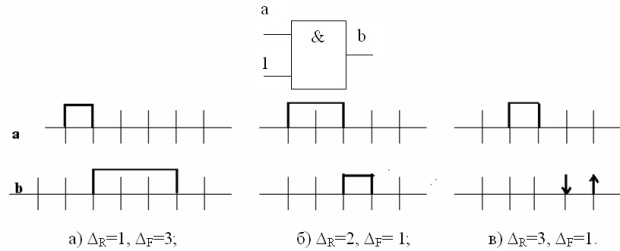
В ряде случаев используют для одного и того же элемента различные значения задержек для переднего и заднего фронтов сигнала. Например, в схемах на МОП-структурах
время задержки спада сигнала  может в 3 раза превышать время задержки переднего фронта
может в 3 раза превышать время задержки переднего фронта  . Следовательно, в данном случае при
моделировании длительность (положительного) импульса может увеличиваться (как это имеет место на рис.4.5а). (
. Следовательно, в данном случае при
моделировании длительность (положительного) импульса может увеличиваться (как это имеет место на рис.4.5а). ( для элементов
для элементов  и
и  для элементов
для элементов  )
)
Соответственно большее значение задержки нарастания фронта по сравнению с задним фронтом может привести к уменьшению длительности импульса (рис.4.6б). Вместе с тем, при некоторых соотношениях времен задержек переднего фронта и спада возможны случаи, когда моделирование показывает невозможные с практической точки зрения события (рис.4.6в), когда задний фронт "обгоняет" передний. Для исключения подобных ситуаций в процессе моделирования следует предусматривать специальные меры.
а) 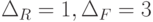 ; б)
; б)  ; в)
; в)  .
.
Определить точное значение задержки для данного типа логического элемента довольно трудно так как всегда существует разброс значений (в силу технологических причин, влияния внешней среды и т.п. ). Поэтому иногда для повышения точности моделирования указывают некоторый диапазон ожидаемых задержек. Такую модель называют моделью с неопределенной задержкой. Модель, в которой в качестве концов диапазона указывают максимальное время задержки  и минимальное время задержки
и минимальное время задержки  , носит название модели с максимальной и минимальной задержками.
, носит название модели с максимальной и минимальной задержками.
В качестве примера рассмотрим распространение сигнала через элемент  . Как показано на рис.4.7 , выходное значение изменяется от
. Как показано на рис.4.7 , выходное значение изменяется от  к
к  при изменении входного сигнала от
при изменении входного сигнала от  к
к  . Однако, поскольку в течение времени
. Однако, поскольку в течение времени  изменения не происходит, а после
изменения не происходит, а после  устанавливается
устанавливается  , то в диапазоне от
, то в диапазоне от  до
до  присваивается неопределенное значение
присваивается неопределенное значение  . Аналогично при моделировании заднего фронта также присваивается неопределенное значение
. Аналогично при моделировании заднего фронта также присваивается неопределенное значение  , как показано на рис.4.7.
, как показано на рис.4.7.
С помощью максимальных и минимальных задержек можно промоделировать большое число сложных временных ситуаций, встречающихся в реальной схеме. Вместе с тем такая модель часто показывает чересчур "пессимистические" результаты, когда большая часть линий схемы принимает неопределенные значения. Аналогичным образом при моделировании с неопределенной задержкой в соответствии с наихудшим случаем каждый раз при прохождении сигнала через элемент диапазон неопределенных значений u расширяется.
В заключение рассмотрим модель инерционной задержки 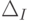 . В понятие инерционной задержки элемента вкладывают следующий смысл. Если на вход элемента
подается входной импульс продолжительностью меньше инерционной задержки
. В понятие инерционной задержки элемента вкладывают следующий смысл. Если на вход элемента
подается входной импульс продолжительностью меньше инерционной задержки 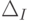 , то элемент не пропускает его (выходной сигнал не изменяется). Введение
такой задержки позволяет моделировать ситуации в реальных схемах, когда элементы не успевают срабатывать на коротких импульсах вследствие своей инерционности (например,
вследствие наличия емкости). Если, например,
, то элемент не пропускает его (выходной сигнал не изменяется). Введение
такой задержки позволяет моделировать ситуации в реальных схемах, когда элементы не успевают срабатывать на коротких импульсах вследствие своей инерционности (например,
вследствие наличия емкости). Если, например,  , то, как показано на рис. 4.8 , при ширине импульса
, то, как показано на рис. 4.8 , при ширине импульса
 (и менее) нельзя получить изменение сигнала на выходе элемента.
(и менее) нельзя получить изменение сигнала на выходе элемента.
Выше были рассмотрены различные виды задержек и связанные с ними проблемы. Для более точного моделирования можно рассматривать сочетания различных видов задержек. Однако это значительно увеличивает время моделирования и неприемлемо с точки зрения практического использования. Реальный путь состоит в том, что следует учитывать влияние задержек с помощью моделей, не вызывающих трудностей при моделировании. Например, можно применять последовательно следующие средства:
- логическая верификация с использованием только модели с единичными задержками;
- моделирование с учетом различных задержек для подъема и спада сигналов;
- моделирование с использованием модели с неопределенной задержкой;
- моделирование с использованием статистических методов вычисления задержки.