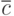|
Добрый день можно поинтересоваться где брать литературу предложенную в курсе ?Большинство книг я не могу найти в известных источниках |
Модели логических элементов
Модели логических элементов в многозначных алфавитах
При построении многозначных моделей элементов используются те же подходы, что и в случае
двоичного алфавита. Рассмотрим сначала моделирование логических элементов в троичном алфавите  . Для примера возьмем 2-входовой вентиль
. Для примера возьмем 2-входовой вентиль 
 . Входы и выход этого элемента принимают значения из троичного алфавита
. Входы и выход этого элемента принимают значения из троичного алфавита 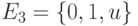 . Пусть входы имеют значения
. Пусть входы имеют значения  . Чему равно значение выхода
. Чему равно значение выхода  в алфавите
в алфавите 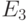 ? Поскольку символ
? Поскольку символ  представляет два значения
представляет два значения  (это
(это  или
или  , но неизвестно, что именно), то моделирование на одном троичном наборе можно выполнить путем моделирования на двух двоичных наборах, покрываемых троичным, и затем сравнить результаты. Для нашего примера имеем:
, но неизвестно, что именно), то моделирование на одном троичном наборе можно выполнить путем моделирования на двух двоичных наборах, покрываемых троичным, и затем сравнить результаты. Для нашего примера имеем:
- значения первого двоичного набора
 (покрываемом троичным) дают
(покрываемом троичным) дают  ;
; - значения второго двоичного набора
 также дают
также дают  .
.
Поскольку значения выхода y для двух двоичных наборов совпадают, то полагаем  (где
(где  – символ троичного алфавита). Для другого входного троичного набора
– символ троичного алфавита). Для другого входного троичного набора  аналогично получаем:
аналогично получаем:
- значения первого двоичного набора
 дают
дают  ;
; - значения второго двоичного набора
 дают
дают 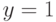 .
.
Поскольку значения y различны для двоичных наборов, покрываемых данным троичным, полагаем значение выхода  . Исходя из подобных соображений и физического смысла, можно построить табличные модели логических элементов в 3- и 5-значном алфавитах.
. Исходя из подобных соображений и физического смысла, можно построить табличные модели логических элементов в 3- и 5-значном алфавитах.
Табличные многозначные модели
В
таблица
4.2,
таблица
4.3,
таблица
4.4 представлены 5-значные модели стандартных 2-входовых вентилей
соответственно  .
.
При этом левый верхний угол таблиц содержит трехзначную часть. Справедливость этих таблиц нетрудно проверить, исходя из смысла символов соответствующего алфавита. При программной реализации обычно символы многозначного алфавита кодируются целыми числами, а таблицы описываются в виде двумерных массивов. Так перекодированная таблица  (
таблица
4.2) будет иметь следующий вид, представленный в табл.4.5.
(
таблица
4.2) будет иметь следующий вид, представленный в табл.4.5.
При этом вычисление значение выхода в многозначном алфавите по заданным значениям входов сводится к выборке нужного элемента в двумерном массиве, так как значения входов определяют индексы этого массива. Пусть, например, для вентиля  модель описана в виде двумерного массива
модель описана в виде двумерного массива ![TAND[0:4, 0:4]](/sites/default/files/tex_cache/edf9e979347ed62288752827c5dac613.png) . При входных значениях
. При входных значениях 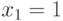 (соответствует символу
(соответствует символу  ) и
) и  (соответствует символу
(соответствует символу  ) получаем
) получаем ![y=TAND[1,2]=2](/sites/default/files/tex_cache/6f26c28579c383c1351c86b466ea6be6.png) , что соответствует неопределенному значению
, что соответствует неопределенному значению  . Ясно, что с ростом числа переменных резко возрастает объем требуемой памяти и метод становится практически непригодным. Следует отметить, что эвристический подход к построению моделей логических элементов в многозначных алфавитах и табличная форма задания модели, сдерживают дальнейшую разработку многозначных моделей для сложных ДУ, реализованных на СБИС. В третьем разделе рассмотрены более подробно вопросы построения многозначных моделей, как на вентильном, так и на функциональном уровне.
. Ясно, что с ростом числа переменных резко возрастает объем требуемой памяти и метод становится практически непригодным. Следует отметить, что эвристический подход к построению моделей логических элементов в многозначных алфавитах и табличная форма задания модели, сдерживают дальнейшую разработку многозначных моделей для сложных ДУ, реализованных на СБИС. В третьем разделе рассмотрены более подробно вопросы построения многозначных моделей, как на вентильном, так и на функциональном уровне.
Компонентные многозначные модели
Данный способ построения многозначных моделей элементов основан на кодировании многозначных алфавитов и является обобщением метода построения моделей, изложенных для двоичного алфавита. Рассмотрим сначала троичные компонентные модели. Так как каждая троичная переменная 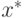 принимает три значения
принимает три значения 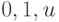 ,то она может быть представлена двумя булевыми переменными, принимающими двоичные значения. Для этого используются различные способы кодирования троичного алфавита
[
2.4
]
. Мы, в основном, будем использовать дизъюнктивный метод кодирования троичного алфавита, представленный табл.4.7.
,то она может быть представлена двумя булевыми переменными, принимающими двоичные значения. Для этого используются различные способы кодирования троичного алфавита
[
2.4
]
. Мы, в основном, будем использовать дизъюнктивный метод кодирования троичного алфавита, представленный табл.4.7.
Здесь переменные 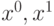 могут принимать только двоичные значения. В современных системах моделирования, как правило, компоненты хранятся в разных машинных словах. Очевидно, что при таком подходе для моделирования логического элемента с троичной функцией
могут принимать только двоичные значения. В современных системах моделирования, как правило, компоненты хранятся в разных машинных словах. Очевидно, что при таком подходе для моделирования логического элемента с троичной функцией 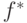 необходимо две булевых функции
необходимо две булевых функции  и
и 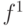 . В табл.4.6 представлены троичные компонентные модели основных вентилей для дизъюнктивного метода кодирования.
. В табл.4.6 представлены троичные компонентные модели основных вентилей для дизъюнктивного метода кодирования.
Известен простой способ построения функций  и
и 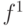 для произвольной булевой функции. Если
для произвольной булевой функции. Если  задана дизъюнктивной нормальной формой (ДНФ), то компонента
задана дизъюнктивной нормальной формой (ДНФ), то компонента 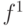 получается из ДНФ функции
получается из ДНФ функции  заменой вхождений переменных
заменой вхождений переменных  на
на  и
и  на
на 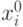 . Аналогично компонента
. Аналогично компонента  получается из ДНФ отрицания функции
получается из ДНФ отрицания функции 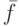 . Например, для функции
. Например, для функции  и
и  имеем
имеем  и
и  .
.
Метод сканирования входов
В большинстве программ моделирования в качестве базовых (элементарных) логических элементов используются простейшие вентили  . Они характеризуются, прежде всего, двумя параметрами: контролирующее значение
. Они характеризуются, прежде всего, двумя параметрами: контролирующее значение  и инверсия
и инверсия  . Значение входа называется контролирующим, если оно определяет выход вентиля, равный
. Значение входа называется контролирующим, если оно определяет выход вентиля, равный  , независимо от значений остальных входов.
таблица
4.9 и
таблица
4.8представляют соответственно простые кубы и значения параметров для любых стандартных 3-входовых вентилей. В табл.4.9 в каждой строке представлен простой куб вентиля в порядке, указанном в табл.4.8.
, независимо от значений остальных входов.
таблица
4.9 и
таблица
4.8представляют соответственно простые кубы и значения параметров для любых стандартных 3-входовых вентилей. В табл.4.9 в каждой строке представлен простой куб вентиля в порядке, указанном в табл.4.8.
Ниже представлен псевдокод типичной программы вычисления значения выхода, реализующей данный метод [ 2.3 ] .

Метод счетчиков
Анализ программы показывает, что для вычисления значения выхода стандартного вентиля в троичном алфавите достаточно знать: имеет ли
какой либо вход контролирующее значение  и при его отсутствии наличие неопределенного значения
и при его отсутствии наличие неопределенного значения  на входах. Поэтому был предложен метод
[
2.3
]
, в котором вместо хранения значений входов для каждого вентиля сохраняются значения двух счетчиков –
на входах. Поэтому был предложен метод
[
2.3
]
, в котором вместо хранения значений входов для каждого вентиля сохраняются значения двух счетчиков –  и
и
 , где содержится число входов с контролирующим и неопределенным значением соответственно. При очередном вызове функции модели вентиля значение этих
счетчиков может изменяться. Например, при изменении
, где содержится число входов с контролирующим и неопределенным значением соответственно. При очередном вызове функции модели вентиля значение этих
счетчиков может изменяться. Например, при изменении 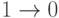 входа вентиля
входа вентиля  счетчик
счетчик  увеличивается на
увеличивается на  , в
то время как при изменении
, в
то время как при изменении  увеличивается на
увеличивается на  счетчик
счетчик  . Тогда вычисление значения выхода вентиля сводится к
проверке счетчиков. Ниже представлен метод вычисления значения выхода.
. Тогда вычисление значения выхода вентиля сводится к
проверке счетчиков. Ниже представлен метод вычисления значения выхода.

Более подробно вопросы построения многозначных моделей логических элементов будут изложены в "Система многозначных алфавитов и функций" , где рассматривается единая система многозначных алфавитов и функций.