Математические методы распознавания образов
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 30.04.2008 | Доступ: свободный | Студентов: 1614 / 251 | Оценка: 4.24 / 3.92 | Длительность: 14:56:00
Тема: Компьютерная графика
Специальности: Математик
Теги: beta, IWR, recognition, алгоритмы, базисными векторами, выпуклая оболочка, выходной нейрон, направляющий вектор, обучение, поиск, полиэдр, пространство признаков, процедуры, разработка, сложность, собственный вектор, теория, эмпирический риск
Лекция 11:

Методы генерации признаков
A
|
версия для печати
< Лекция 10 || Лекция 11: 123456 || Лекция 12 >

11.4. Преобразования Адамара и Хаара

Преобразование Адамара и Хаара имеют такие же вычислительные достоинства, как и ДПФ, ДКП, ДСП. Их матрицы состоят из \pm 1, поэтому они вычисляются через сложения и вычитания без умножений.

11.4.1. Преобразование Адамара

Определение. Унитарная матрица Адамара порядка n – это N\times N матрица, где N=2^n, сгенерированная по следующему итерационному правилу

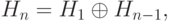
H_n=H_1\oplus H_{n-1},
где
H_1=\frac{1}{\sqrt{2}} \begin{pmatrix} 1&1\\ 1&-1 \end{pmatrix}
и \oplus обозначает кронекерово произведение двух матриц:
A\oplus B= \begin{pmatrix} A(1,1)B&A(1,2)B&\ldots&A(1,N)B\\ A(2,1)B&A(2,2)B&\ldots&A(2,N)B\\ \vdots&\vdots&\ddots&\ldots\\ A(N,1)B&A(N,2)B&\ldots&A(N,N)B \end{pmatrix}.

Распишем 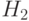H_2:

H_2=H_1\oplus H_1=\frac12 \begin{pmatrix} 1&1&1&1\\ 1&-1&1&-1\\ 1&1&-1&-1\\ 1&-1&-1&1 \end{pmatrix}.

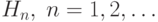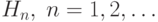По аналогии можно выписать все H_n,\;n=1,2,\ldots. Нетрудно установить ортогональность H_n,\;n=1,2,\ldots:

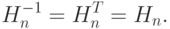
H_n^{-1}=H_n^T=H_n.

Для вектора x из N образцов пара преобразований есть: y=H_nx,\; x=H_ny

Преобразование Адамара имеет очень хорошие "упаковочные" свойства. Алгоритм для вычисления выделений и сложений достаточно быстрый: O(N-\ln N).

11.4.2. Преобразование Хаара

Начальной точкой для определения преобразования Хаара являются функции Хаара, которые являются непрерывными и определенными на замкнутом сегменте [0,1].

Порядок k функций Хаара единственным образом раскладывается через два целых числа p и q:

k=2^p+q-1,\;k=0,1\ldots,L-1,\;L=2^n,

Определение. Функции Хаара:

\begin{aligned} &h_0(z)\equiv h_{00}(z)=\frac{1}{\sqrt{L}},\;z\in[0,1];\\ &h_k(z)\equiv h_{pq}(z)=\frac{1}{\sqrt{L}}\cdot \left\{ \begin{aligned} &2^{\frac{p}{2}},\text{ при }\frac{q-1}{2^p}\leq z<\frac{q-0.5}{2^p},\\ &-2^{\frac{p}{2}},\text{ при }\frac{q-0.5}{2^p}\leq z<\frac{q}{2^p},\\ &0,\text{ для остальных } z\in[0,1]. \end{aligned} \right. \end{aligned}

Дальше >>
< Лекция 10 || Лекция 11: 123456 || Лекция 12 >

Вопросы и ответы

вопросов: 0