Селекция признаков
10.4. Векторная селекция признаков. Мера отделимости классов
Ранее обсуждались дискриминантные свойства отдельных признаков. Теперь рассмотрим дискриминантные способности векторов признаков.
Пусть
-
 – множество признаков,
– множество признаков, -
 – подмножество из
– подмножество из  признаков,
признаков, -
 – мера отделимости классов на множестве признаков
– мера отделимости классов на множестве признаков  .
.
Тогда задача выглядит следующим образом:
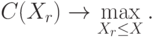
Существует различные подходы к описанию меры отделимости. Мы рассмотрим два таких подхода:
- Дивергенция
- Матрица рассеивания.
10.4.1. Дивергенция. Будем рассматривать Байесовское правило:

 . Ошибка классификации задается следующим интегралом:
. Ошибка классификации задается следующим интегралом:![P_l=P(\Omega_0)-\int\limits_{R_1}[P(\Omega_1|x)-P(\Omega_0|x)]p(x)dx](/sites/default/files/tex_cache/64634c7768208f90031c155014497246.png)
Пусть
-
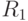 – область решения по классу
– область решения по классу  ; если
; если  , то класс
, то класс  ;
; -
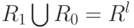 – все пространство признаков,
– все пространство признаков, -
 – очень важный показатель разделимости классов. От этой разности зависит ошибка классификации;
– очень важный показатель разделимости классов. От этой разности зависит ошибка классификации; -
 – информация о разделяющих свойствах вектора признаков (другая форма этого показателя).
– информация о разделяющих свойствах вектора признаков (другая форма этого показателя).
Информацию о разделяющих свойствах вектора признаков можно записать следующим образом:
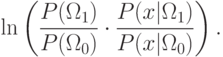
Если

![\int_{-\infty}^{+\infty}
\left[
\ln\frac{p(x|\Omega_1)}{p(x|\Omega_0)}
\right]
p(x|\Omega_1)dx=D_{01}](/sites/default/files/tex_cache/e377ce17c0b16389bf11c554d6db67d2.png)
 – характеристика отделимости. Аналогично:
– характеристика отделимости. Аналогично:![D_{10}=\int\limits_{-\infty}^{+\infty}
\left[
\ln\frac{p(x|\Omega_0)}{p(x|\Omega_1)}
\right]
p(x|\Omega_0)dx.](/sites/default/files/tex_cache/a6042e6314e831ab30c1397c220e5e58.png)
Обозначим через  дивергенцию разделения классов по вектору
признаков
дивергенцию разделения классов по вектору
признаков  . Аналогично для случая многоклассовой задачи
. Аналогично для случая многоклассовой задачи  –
дивергенция классов
–
дивергенция классов 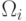 и
и  . Тогда
. Тогда
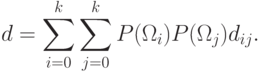
Дивергенция есть мера расстояния между плотностями. Она имеет следующие свойства:
 при
при  .
Если компоненты вектора признаков независимы, можно показать, что
.
Если компоненты вектора признаков независимы, можно показать, что  .
.
Дивергенция учитывает различия и в средних, и в дисперсии. Однако, она очень чувствительна к разности средних, что затрудняет использование.
10.4.2. Мера на основе матриц рассеивания
Главный недостаток многих критериев отделимости классов – сложность вычисления, если не проходит предположение о гауссовых плотностях. Мы рассмотрим простой критерий, не требующий нормальности распределения, построенный на информации, относящейся к тому, как вектора признаков разбросаны в пространстве.
Пусть
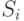 – матрица ковариации,
– матрица ковариации,  ,
где
,
где  – вектор признаков и
– вектор признаков и 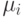 – среднее
значение по
– среднее
значение по  , принадлежащим данному классу,
, принадлежащим данному классу,  .
.
 – матрица внутриклассового рассеивания есть мера дисперсии
признаков, где
– матрица внутриклассового рассеивания есть мера дисперсии
признаков, где 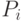 – априорная вероятность данного класса,
– априорная вероятность данного класса,  .
.
 – матрица внеклассового рассеивания, где
– матрица внеклассового рассеивания, где  – общее среднее –
разброс относительно общего среднего всех классов (центр тяжести).
– общее среднее –
разброс относительно общего среднего всех классов (центр тяжести).
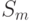 – смешанная матрица рассеивания (ковариация относительно общего
среднего),
– смешанная матрица рассеивания (ковариация относительно общего
среднего),  .
.
Определение. Следом (обозначается 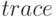 )
называется сумма диагональных элементов матрицы.
)
называется сумма диагональных элементов матрицы.
Пример. Пусть задана матрица  .
Тогда
.
Тогда  .
.
Пусть  – критерий,
принимающий большие значения, когда образы хорошо
кластеризуются вокруг своих средних в границах каждого класса и
кластеры разных классов хорошо разделены. Иногда вместо
– критерий,
принимающий большие значения, когда образы хорошо
кластеризуются вокруг своих средних в границах каждого класса и
кластеры разных классов хорошо разделены. Иногда вместо 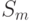 используют
используют  .
Тогда получаем задачу
.
Тогда получаем задачу 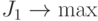 .
.
Вместо критерия  можно использовать другие критерии:
можно использовать другие критерии:

Последний критерий очень удобен на практике для аналитических выкладок.
10.4.3. Стратегия наращивания вектора признаков. Стратегия наращивания вектора признаков заключается в использовании признаков, дающих наибольший прирост меры отделимости.
Рассмотрим алгоритм наращивания вектора признаков. Пусть из 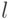 признаков нужно отобрать
признаков нужно отобрать  .
.
Рассмотрим множество признаков  ,.
Необходимо найти признак, имеющий наибольшую селективную способность.
Это аналогично нахождению
,.
Необходимо найти признак, имеющий наибольшую селективную способность.
Это аналогично нахождению  . Пусть
. Пусть  ,
где
,
где  .
.
Пусть  – построенное множество признаков.
Далее,
– построенное множество признаков.
Далее,  .
.
Условие остановки:  , либо
, либо  .
.
10.4.4. Стратегия сокращения вектора признаков
Пусть  – множество признаков.
– множество признаков.
Шаг алгоритма: набор признаков  , чтобы выполнялось
, чтобы выполнялось  и
и  .
.
Условие остановки:  , либо
, либо  .
.
10.4.5. Выбор стратегии
Пусть 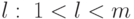 . Если
. Если  ,
то используем стратегию сокращения вектора признаков. Если
,
то используем стратегию сокращения вектора признаков. Если  , то используем стратегию наращивания вектора
признаков.
, то используем стратегию наращивания вектора
признаков.
В качестве альтернативы можно использовать сравнение  с
с 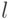 .
Если
.
Если  , то используем стратегию сокращения вектора признаков.
Если
, то используем стратегию сокращения вектора признаков.
Если  , то используем стратегию наращивания вектора признаков.
, то используем стратегию наращивания вектора признаков.
Обе стратегии являются жадными.
Определение. Стратегия называется "жадной", если она не допускает шагов возврата.
10.4.6. Алгоритм плавающего поиска. Примером нежадной стратегии является метод плавающего поиска. Плавающий поиск базируется на стратегии вставки и исключения.
Пусть все признаки упорядочены по убыванию меры  .
Пусть также
.
Пусть также 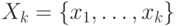 – первые
– первые  признаков, имеющие наибольшее
признаков, имеющие наибольшее  . Тогда остальные признаки
строятся следующим образом:
. Тогда остальные признаки
строятся следующим образом:

Предположим, что построены множества  .
Рассмотрим алгоритм плавающего поиска.
.
Рассмотрим алгоритм плавающего поиска.
Шаг 1. Вставка.
Добавление признаков:  и
и  .
.
Шаг 2. Проверка
 ,
где
,
где  – признак дающий наименьший вклад (минимальные потери при выбросе).
– признак дающий наименьший вклад (минимальные потери при выбросе).
Если  , то увеличиваем
, то увеличиваем  и переходим на шаг 1.
и переходим на шаг 1.
Если  и
и 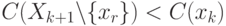 , то переходим на шаг 1.
, то переходим на шаг 1.
Если  , то
, то  и переходим на шаг 1.
и переходим на шаг 1.

Поиск наименее значительного элемента в новом множестве 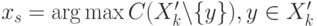 .
.
Если 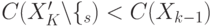 , то
, то  и переходим на шаг 1.
и переходим на шаг 1.
Если  , то уменьшаем
, то уменьшаем  на 1.
на 1.
Если  , то
, то  ,
,  и переходим на шаг 1.
и переходим на шаг 1.
Переходим на шаг 3.

