Метод потенциальных функций
6.2. Выбор системы функций
 .
Система функций
.
Система функций  задается априорно.
Обычно используют некую полную систему функций, например, на конечном
отрезке можно взять систему тригонометрических функций. Эта система к
тому же ортогональна.
задается априорно.
Обычно используют некую полную систему функций, например, на конечном
отрезке можно взять систему тригонометрических функций. Эта система к
тому же ортогональна.
Утверждение. Если задана полная ортогональная система функций одной переменной, то можно построить полную ортогональную систему функций любого числа переменных.
Доказательство. Пусть  –
полная ортогональная система функций на конечном интервале
–
полная ортогональная система функций на конечном интервале  .
Рассмотрим систему
.
Рассмотрим систему

Эта система полна и ортогональна на декартовом произведении 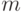 экземпляров
экземпляров  , то есть на
, то есть на 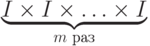 ..
..
Проверим ортогональность. В скалярном произведении двух различных функций 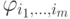 и
и  :
:
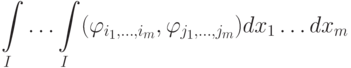
 , что
, что 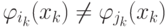 и,
в силу ортогональности системы
и,
в силу ортогональности системы  , имеем:
, имеем:
Далее, пусть  – произвольная функция
– произвольная функция 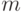 переменных. Фиксируем все
переменные, кроме
переменных. Фиксируем все
переменные, кроме 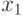 , и получаем разложение функции
, и получаем разложение функции 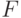 :
:

Повторяем это рассуждение для  последовательности
последовательности  раз:
раз:


6.3. Сходимость общей рекуррентной процедуры
Предположим, что
обучающая последовательность есть выборка конечного объема из
пространства  (
(  – пространство признаков). Тогда последовательность
– пространство признаков). Тогда последовательность  есть последовательность случайных функций, и последовательность
есть последовательность случайных функций, и последовательность 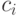 –
последовательность случайных чисел. Поэтому будем говорить о
сходимости
–
последовательность случайных чисел. Поэтому будем говорить о
сходимости  в вероятностном смысле, то есть либо по вероятности, либо
с вероятностью равной 1, либо в среднем.
в вероятностном смысле, то есть либо по вероятности, либо
с вероятностью равной 1, либо в среднем.
Пусть 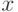 – случайные величины из
– случайные величины из  , а
, а  – выборка для конечного объекта.
– выборка для конечного объекта.
Теорема. Пусть заданы два множества  и
и  и выполнены следующие условия.
и выполнены следующие условия.
-
Существует функция
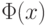 такая, что
такая, что  , при
, при 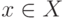 ,
,  при
при  , где константа
, где константа  .
. -
Задана система функций
 такая, что
такая, что  ,
,  ,
, 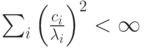
-
Точки из обучающей последовательности
независимые случайные величины, с одной и той же плотностью
 . Тогда общая рекуррентная
процедура, определяемая формулой
. Тогда общая рекуррентная
процедура, определяемая формулой  , где
, где  исходится в следующем смысле:
исходится в следующем смысле:
![\texttt{E}\left[|sign\Phi(x)-sign\Phi_n(x)|\right]\rightarrow 0](/sites/default/files/tex_cache/27bdea017297fe1939190f5558fa99f2.png) , при
, при  .
.
Теорема. Пусть выполнены все условия предыдущей теоремы.
Пусть также на каждом  -ом шаге работы общей рекуррентной
процедуры существует строго положительная вероятность исправления
ошибки, если функция
-ом шаге работы общей рекуррентной
процедуры существует строго положительная вероятность исправления
ошибки, если функция  к
к  -ому шагу
еще не разделила классы
-ому шагу
еще не разделила классы  и
и  . Пусть с
вероятностью единица для каждой реализации процедуры существует
конечное число
. Пусть с
вероятностью единица для каждой реализации процедуры существует
конечное число  такое, что
такое, что
 – правильно разделяет
– правильно разделяет  и
и  ,
,
 – конечный интервал на прямой
– конечный интервал на прямой  ,
,
 – полная ортогональная система функций,
– полная ортогональная система функций,  ,
,
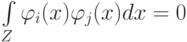 при
при  .
.
Тогда система функций  полна и ортогональна на пространстве
полна и ортогональна на пространстве  .
.
Доказательство. Ортогональность очевидна. Докажем полноту. Пусть  – произвольная функция в
– произвольная функция в  такая,
что
такая,
что  . Фиксируем переменные начиная
с
. Фиксируем переменные начиная
с  , тогда
, тогда

6.4. Функции Эрмита
Если в качестве системы функций  взять функции вида
взять функции вида

 – полином Эрмита.
– полином Эрмита.Тогда
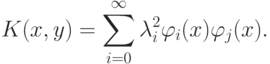
Обозначим 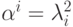 , где
, где 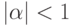 , тогда
, тогда
![K(x,y)=\frac{1}{\sqrt{\pi(1-\alpha)^2}}\exp\left[\frac{2xy\alpha-(x^2+y^2)\alpha^2}{1-\alpha^2}\right].](/sites/default/files/tex_cache/5733a87c2338b34ff51977e25dc41653.png)
