Предварительные сведения
События и операции над ними
Пространство элементарных исходов. Основным понятием теории вероятностей является множество всех возможных результатов данного случайного эксперимента.
Определение 1. Пространством элементарных исходов
называется множество  , содержащее все возможные взаимоисключающие
результаты данного случайного эксперимента.
Элементы множества
, содержащее все возможные взаимоисключающие
результаты данного случайного эксперимента.
Элементы множества  называются элементарными исходами
и обозначаются буквой
называются элементарными исходами
и обозначаются буквой 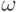 .
.
Отметим сразу, что любое непустое множество  можно считать пространством
элементарных исходов какого-то случайного эксперимента.
можно считать пространством
элементарных исходов какого-то случайного эксперимента.
Определение 2.
Событиями называются подмножества множества  .
Говорят, что произошло событие
.
Говорят, что произошло событие  ,
если эксперимент завершился одним из элементарных исходов,
входящих в множество
,
если эксперимент завершился одним из элементарных исходов,
входящих в множество  .
.
Замечание.
Вообще говоря, можно называть событиями не любые
подмножества множества  , а лишь элементы
некоторого набора подмножеств.
О смысле такого ограничения мы поговорим позднее.
, а лишь элементы
некоторого набора подмножеств.
О смысле такого ограничения мы поговорим позднее.
Итак, элементарный исход - это мельчайший неделимый результат эксперимента, а событие может состоять из одного или нескольких исходов.
Напомним, что конечные и счетные множества удобно задавать перечислением
их элементов. Например,  - множество, состоящее из первых
ста натуральных чисел. Несчетные множества
обычно задают указанием свойства, которым обладают все элементы
множества. Так,
- множество, состоящее из первых
ста натуральных чисел. Несчетные множества
обычно задают указанием свойства, которым обладают все элементы
множества. Так,  -
множество действительных чисел из интервала
-
множество действительных чисел из интервала  .
.
Пример 1.
Один раз подбрасывают игральную кость.
Рассмотрим пространство элементарных исходов 

 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
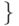 Элементарные исходы здесь
соответствуют числу выпавших очков.
Элементарные исходы здесь
соответствуют числу выпавших очков.
Событие 

 ,
,
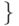 произойдет, если выпадет
одно или два очка; событие
произойдет, если выпадет
одно или два очка; событие 

 ,
,
 ,
,
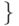 означает, что выпадет нечетное число очков. Событие
означает, что выпадет нечетное число очков. Событие 

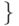 состоит из одного элементарного исхода и означает появление шести очков.
состоит из одного элементарного исхода и означает появление шести очков.
Пример 2.
Подбрасываются две игральные кости. Будем считать их различимыми и назовем одну
из них первой, другую - второй.
Пространством элементарных исходов является множество пар чисел  где
где  - число очков, выпавших на первой
кости,
- число очков, выпавших на первой
кости,  - на второй.
- на второй.  .
В этом множестве
.
В этом множестве  элементарных исходов:
элементарных исходов:
![\begin{equation}
\begin{matrix}
(1,1) & (1,2) & \cdots & (1,6) \\
(2,1) & (2,2) & \cdots & (2,6) \\
\hdotsfor[1.5]{4} \\
(6,1) & (6,2) & \cdots &(6,6)
\end{matrix}
\end{equation}](/sites/default/files/tex_cache/93d9174df16be50d4b506c0a72f7fc9f.png) |
( 1.1) |
Заметим, что для симметричных костей
все эти  исходов равновозможны:
ни одна из этих комбинаций не имеет больше шансов выпасть, чем другая.
Действительно, на первой кости с равными шансами выпадает любая грань.
Это означает, что результат бросания двух костей имеет столько же шансов оказаться
в первой строке матрицы ( 1 ), что и во второй, в третьей и т. д.
Но на второй кости снова с одинаковыми шансами
выпадает любая грань, поэтому и каждое место в строке равновозможно.
исходов равновозможны:
ни одна из этих комбинаций не имеет больше шансов выпасть, чем другая.
Действительно, на первой кости с равными шансами выпадает любая грань.
Это означает, что результат бросания двух костей имеет столько же шансов оказаться
в первой строке матрицы ( 1 ), что и во второй, в третьей и т. д.
Но на второй кости снова с одинаковыми шансами
выпадает любая грань, поэтому и каждое место в строке равновозможно.
Событие "на первой кости выпадет одно очко" можно записать так:  ; событие "на второй кости выпадет одно очко" запишется так:
; событие "на второй кости выпадет одно очко" запишется так:  ; событие
; событие  означает, что
сумма выпавших очков равна четырем; событие
означает, что
сумма выпавших очков равна четырем; событие  - на костях выпадет одинаковое число очков.
- на костях выпадет одинаковое число очков.
Пример 3. Подбрасываются две неразличимые игральные кости.
Элементарными исходами будем считать пары чисел  где
где  . Например, элементарный исход
. Например, элементарный исход  случается, если на одной из костей выпадает одно очко, на другой -
два очка. В множестве
случается, если на одной из костей выпадает одно очко, на другой -
два очка. В множестве  двадцать один исход:
двадцать один исход:
![\begin{matrix}
(1,1) & (1,2) & \cdots & (1,6) \\
& (2,2) & \cdots & (2,6) \\
& \hdotsfor[1.5]{2} \\
& & & (6,6)
\end{matrix}](/sites/default/files/tex_cache/db0083d0f7cdb270105cc7cf0b22ab01.png)
Для симметричных костей эти исходы равновозможными уже не будут: например,
исход  имеет вдвое больше шансов появиться, чем исход
имеет вдвое больше шансов появиться, чем исход 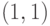 .
Мы просто перестали различать исходы из примера 2,
симметричные друг другу относительно главной диагонали матрицы (1).
.
Мы просто перестали различать исходы из примера 2,
симметричные друг другу относительно главной диагонали матрицы (1).
Теперь событие "сумма выпавших очков равна четырем"
состоит из двух элементарных исходов 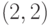 и
и  .
Событие "на костях выпадет одинаковое число очков" по-прежнему включает
шесть исходов.
Слова "на первой кости выпадет одно очко"
никакого события уже не описывают, а
событие
.
Событие "на костях выпадет одинаковое число очков" по-прежнему включает
шесть исходов.
Слова "на первой кости выпадет одно очко"
никакого события уже не описывают, а
событие  означает,
что хотя бы на одной из костей выпало одно очко (ср. с примером 2).
означает,
что хотя бы на одной из костей выпало одно очко (ср. с примером 2).
Пример 4. На поверхность стола бросается монета. Результатом эксперимента можно считать положение центра монеты. Пространство элементарных исходов такого эксперимента - множество всех точек стола. Оно бесконечно и несчетно. Событием можно назвать, например, попадание центра монеты на лист бумаги, лежащий на столе, в левую или правую половину стола.
Пример 5.
Монета подбрасывается до тех пор, пока не выпадет вверх гербом.
Пространство элементарных исходов является бесконечным, но счетным множеством:  ,
где
,
где 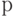 означает выпадение решки, а
означает выпадение решки, а  - выпадение герба
при одном подбрасывании.
Событие "герб выпал при броске с четным номером" выглядит так:
- выпадение герба
при одном подбрасывании.
Событие "герб выпал при броске с четным номером" выглядит так:
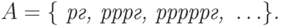
Пример 6. В коробке лежат один черный и два белых шара. Из коробки достают наугад один шар.
Можно определить два разных пространства элементарных исходов. Первое из
них состоит из двух исходов 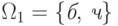 -
мог появиться белый шар или черный. Эти исходы, очевидно, не будут равновозможными:
появление белого шара вдвое вероятнее, чем появление черного.
-
мог появиться белый шар или черный. Эти исходы, очевидно, не будут равновозможными:
появление белого шара вдвое вероятнее, чем появление черного.
Если мы хотим иметь дело с равновозможными элементарными исходами,
шары следует занумеровать (или различать как-нибудь иначе). Тогда множество 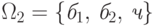 будет состоять из трех равновозможных элементарных исходов.
будет состоять из трех равновозможных элементарных исходов.
Пример 7. В коробке лежат один черный и два белых шара. Из коробки достают наугад два шара. Порядок следования шаров нам безразличен. Занумеруем шары, чтобы элементарные исходы были равновозможными (это может оказаться удобным). Пространство элементарных исходов состоит из трех элементов:

Событие "вынуты два белых шара" включает один исход  а событие "вынуты разноцветные шары" состоит из двух исходов:
а событие "вынуты разноцветные шары" состоит из двух исходов: 
 .
.
Можно, как в примере 6,
рассмотреть пространство элементарных исходов, состоящее из двух
элементов:  -
вынуты два белых шара или шары разных цветов.
Но в таком пространстве второй исход имеет вдвое больше шансов случиться, чем
первый.
-
вынуты два белых шара или шары разных цветов.
Но в таком пространстве второй исход имеет вдвое больше шансов случиться, чем
первый.
