НОУ ИНТУИТ | Введение в математическое моделирование. Лекция 10: Моделирование многомерных нелинейных систем.

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Донецкий национальный технический университет

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 6117 / 2250 | Оценка: 4.11 / 3.78 | Длительность: 12:32:00

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Математик

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции рассматриваются методы решения систем нелинейных уравнений.

Ключевые слова: системы нелинейных уравнений, евклидово пространство, область сходимости, Метод простых итераций, решение систем нелинейных уравнений методом Ньютона, линеаризация, решение системы линейных уравнений, матричная форма, матрица Якоби, метод Ньютона

В задачах проектирования и исследования поведения реальных объектов, процессов и систем (ОПС) математические модели должны отображать реальные физические нелинейные процессы. При этом эти процессы зависят, как правило, от многих переменных.

В результате математические модели реальных ОПС описываются системами нелинейных уравнений.

Решение систем нелинейных уравнений

Дана система нелинейных уравнений

$\left\{ \begin{array}{l} f_1(x_1,x_2,x_3, \ldots, x_n)=0,\\ f_2(x_1,x_2,x_3, \ldots, x_n)=0,\\ \ldots\\ f_n(x_1,x_2,x_3, \ldots, x_n)=0, \end{array} \right.$

( 10.1)

или

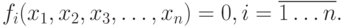
$f_i(x_1,x_2,x_3, \ldots, x_n)=0, i=\overline{1 \ldots n}.$

Необходимо решить эту систему, т.е. найти вектор $\bar X=[x_1,x_2,x_3,\ldots,x_n]$ , удовлетворяющий системе (10.1) с точностью $\varepsilon$ .

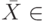Вектор $\bar X$ определяет точку в n-мерном Евклидовом пространстве, т.е. $\bar X \in$ этому пространству и удовлетворяет всем уравнениям системы (10.1).

В отличие от систем линейных уравнений для систем нелинейных уравнений неизвестны прямые методы решения. При решении систем нелинейных уравнений используются итерационные методы. Эффективность всех итерационных методов зависит от выбора начального приближения (начальной точки), т.е. вектора $\overline{X^0}=[x_1^0,x_2^0,\ldots,x_n^0]$ .

Область, в которой начальное приближение 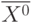$\overline{X^0}$ сходится к искомому решению, называется областью сходимости G. Если начальное приближение 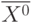$\overline{X^0}$ лежит за пределами G, то решение системы получить не удается.

Выбор начальной точки 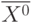$\overline{X^0}$ во многом определяется интуицией и опытом специалиста.

Метод простых итераций

Для применения этого метода исходная система (10.1) должна быть преобразована к виду

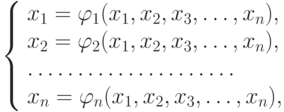$\left\{ \begin{array}{l} x_1=\varphi_1(x_1,x_2,x_3, \ldots, x_n),\\ x_2=\varphi_2(x_1,x_2,x_3, \ldots, x_n),\\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots\\ x_n=\varphi_n(x_1,x_2,x_3, \ldots, x_n), \end{array} \right.$

( 10.2)

или

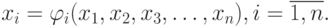
$x_i=\varphi_i(x_1,x_2,x_3, \ldots, x_n), i=\overline{1,n}.$

Далее, выбрав начальное приближение $\overline{X^0}=[x_1^0,x_2^0,\ldots,x_n^0]$ и используя систему (10.2), строим итерационный процесс поиска по схеме:

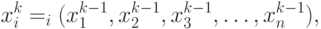
$x_i^k=\varphy_i(x_1^{k-1},x_2^{k-1},x_3^{k-1}, \ldots, x_n^{k-1}),$

т.е. на каждом k-ом шаге поиска вектор переменных $\overline{X}$ находим, используя значения переменных, полученных на шаге (k-1).

Итерационный процесс поиска прекращается как только выполнится условие

$\left|x_j^k – x_j^{k-1}\right| \le \varepsilon, j=\overline{1,n}.$

( 10.3)

При этом условие (10.3) должно выполняться одновременно по всем переменным.

Метод простых итераций используется для решения таких систем линейных уравнений, в которых выполняется условие сходимости итерационного процесса поиска, а именно:

$\sum \limits_{i=1}^{n} \left| \frac{\delta \varphi_i}{\delta x_j} \right| < 1, j=\overline{1,n}.$

( 10.4)

т.е. сумма абсолютных величин частных производных всех преобразованных уравнений системы (10.2) по j-ой переменной меньше единицы.

На рисунке 10.1 представлена схема алгоритма решения систем нелинейных уравнений методом простых итераций.

Рис. 10.1. Схема алгоритма метода простых итераций

Дальше >>

Авторизоваться

Введение в математическое моделирование

Моделирование многомерных нелинейных систем.

Решение систем нелинейных уравнений

Метод простых итераций

Вопросы и ответы