Численные методы решения нелинейных уравнений

Метод половинного деления

Дано нелинейное уравнение:

( 4.1)

Найти корень уравнения, принадлежащий интервалу [a,b], с заданной точностью .

Для уточнения корня методом половинного деления последовательно осуществляем следующие операции:

1. Делим интервал пополам:
   
2. В качестве нового интервала изоляции принимаем ту половину интервала, на концах которого функция имеет разные знаки (рис.4.4).
   

   
   Рис. 4.4.

   Для этого:

   a) Вычисляем значение функции f(x) в точках a и t.

   b) Проверяем: если f(a)f(t) < 0, то корень находится в левой половине интервала [a,b] (рис.4.4.а). Тогда отбрасываем правую половину интервала и делаем переприсвоение b=t.

   c) Если f(a)f(t) < 0 не выполняется, то корень находится в правой половине интервала [a,b] (рис.4.4.б). Тогда отбрасываем левую половину и делаем переприсвоение a=t. В обоих случаях мы получим новый интервал [a,b] в 2 раза меньший предыдущего.
3. Процесс, начиная с пункта 1, циклически повторяем до тех пор, пока длина интервала [a,b] не станет равной либо меньшей заданной точности, т.е.
   

Схема алгоритма уточнения корней по методу половинного деления представлена на рис. 4.5.

Рис. 4.5. Схема алгоритма уточнения корней по методу половинного деления

Метод простых итераций

В ряде случаев весьма удобным приемом уточнения корня уравнения является метод последовательных приближений (метод итераций).

Пусть с точностью необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.

Для применения этого метода исходное уравнение f(x)=0 должно быть приведено к виду

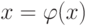( 4.2)

В качестве начального приближения 0 выбираем любую точку интервала [a,b].

Далее итерационный процесс поиска корня строится по схеме:

( 4.3)

В результате итерационный процесс поиска реализуется рекуррентной формулой (4.3). Процесс поиска прекращается, как только выполняется условие

( 4.4)

или число итераций превысит заданное число N.

Для того, чтобы последовательность х₁, х₂,…, х_n приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:

( 4.5)

Рис. 4.6. Геометрический смысл метода

Переходим к построению схемы алгоритма (рис. 4.7). Вычисление функции 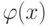оформим в виде подпрограммы.

Рис. 4.7. Схема алгоритма уточнения корня методом итераций