Алгоритмы асимметричного шифрования
Алгоритм RSA
Описание алгоритма
Диффи и Хеллман определили новый подход к шифрованию, что вы-звало к жизни разработку алгоритмов шифрования, удовлетворяющих тре-бованиям систем с открытым ключом. Одним из первых результатов был алгоритм, разработанный в 1977 году Роном Ривестом, Ади Шамиром и Леном Адлеманом и опубликованный в 1978 году. С тех пор алгоритм Rivest-Shamir-Adleman (RSA) широко применяется практически во всех приложениях, использующих криптографию с открытым ключом.
Алгоритм основан на использовании того факта, что задача факторизации является трудной, т.е. легко перемножить два числа, в то время как не существует полиномиального алгоритма нахождения простых сомножителей большого числа.
Алгоритм RSA представляет собой блочный алгоритм шифрования, где зашифрованные и незашифрованные данные являются целыми между 0 и n–1 для некоторого n.
Алгоритм, разработанный Ривестом, Шамиром и Адлеманом, использует выражения с экспонентами. Данные шифруются блоками, каждый блок рассматривается как число, меньшее некоторого числа n. В результате шифрования числа М, М < n, получается число С.

Расшифрование выполняется следующим образом:

Как отправитель, так и получатель должны знать число n. Отправитель знает число, получатель знает число d. Таким образом, открытый ключ есть KU = {e, n} и закрытый ключ есть KR = {d, n}. При этом должны выполняться следующие условия:
- Возможность найти значения е, d и n такие, что Med = M (mod n) для всех М < n.
- Относительно легко вычислить Ме и Сd для всех значений М < n.
- Невозможность определить d, зная е и n.
Сначала рассмотрим первое условие. Нам необходимо выполнение равенства:

Рассмотрим некоторые математические понятия, свойства и теоремы, которые позволят нам определить e, d и n.
- Если а · b = a·c (mod n), то b = c (mod n), если а и n взаимнопростые, т.е НОД (a, n) = 1.
- Обозначим Zp - все числа, взаимнопростые с p и меньшие p. Если p - простое, то Zp - это все остатки. Обозначим w-1 такое число, что w · w-1 = 1 (mod p).
Тогда ∀ w ∈ Zp∃ z: w · z = 1 (mod p)
Доказательство этого следует из того, что т.к. w и p взаимнопростые, то при умножении всех элементов Zp на w по модулю р остатками будут все элементы Zp, возможно, переставленные. Таким образом, хотя бы один остаток будет равен 1.
- Определим функцию Эйлера следующим образом: ϕ(n)- число положительных чисел, меньших n и взаимнопростых с n. Если p - простое, то ϕ (р) = p-1.
Покажем, что если p и q - простые, то ϕ(p · q) = (p-1)·(q-1).
Перечислим числа, меньшие p · q, которые не являются взаимнопросты-ми с p · q:
Числа, которые делятся на р: {p, 2·p, ..., (q-1)·p}. Таких чисел (q – 1).
Числа, которые делятся на q: {q, 2·q, ..., (p-1)·q}. Таких чисел (р - 1).
Таким образом
ϕ(p·q) = p·q - 1 - [(q-1)+(p-1)] = p·q - (p+q) + 1 = (p-1)·(q-1)
-
Теорема Ферма
an-1 = 1 (mod n), если n - простое.
Если все элементы Zn умножить на а по модулю n, то в результате получим все элементы Zn, быть может, в другом порядке. Рассмотрим следующие числа:
{a (mod n), 2·a (mod n), ·, (n-1)·a (mod n)} являются числами {1, 2, ..., (n-1)}, быть может, в некотором другом порядке. Теперь перемножим по модулю n числа из этих двух множеств.
![[(a (mod \quadn)) \cdot (2a (mod\quad n)) \cdot ... \cdot (n-1)a (mod\quad n)] (mod\quad n) =\\ (n-1)! (mod\quad n)
(n-1)! an-1 = (n-1)! (mod\quad n)](/sites/default/files/tex_cache/482b4be0f270d92683cdb1651a2315b2.png)
n и (n-1)! являются взаимнопростыми, если n – простое.
Следовательно, an-1 = 1 (mod n).
-
Теорема Эйлера
aϕ(n) = 1 (mod n)для всех взаимнопростых a и n.
Это верно, если n - простое, т.к. в этом случае ϕ(n) = n-1. Рассмотрим множество R = {x1, x2,..., xf(n)}. Теперь умножим по модулю n каждый элемент этого множества на a. Получим множество S = {a·x1 (mod n), a·x2 (mod n), ..., a·xϕ(n) (mod n)}. Это множество является перестановкой множества R по следующим причинам.
Так как а является взаимнопростым с n и xi являются взаимнопростыми с n, то a· xi также являются взаимнопростыми с n. Таким образом, S - это множество целых, меньших n и взаимнопростых с n.
В S нет дублей, т.к. если a · xi (mod n) = a·xj (mod n) · xi = xj.
Следовательно, перемножив элементы множеств S и R, получим:

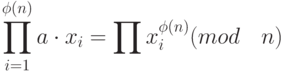

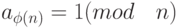
Теперь рассмотрим сам алгоритм RSA. Пусть p и q - простые.

Надо доказать, что

Если НОД (M, n) = 1, то равенство выполняется. Теперь предположим, что НОД (M, n) ≠ 1, т.е. НОД (M, p · q) ≠ 1. Пусть НОД (M, p) ≠ 1, т.е. M = c · p, следовательно НОД (M, q) = 1, так как в противном случае M = c · p и M = l · q, но по условию M < p · q.
Следовательно,

По определению модуля это означает, что M ϕ(n) = 1 + k· q. Умножим обе части равенства на M = c · p. Получим M ϕ(n)+1 = c·p + k·q·c·p.

Таким образом, следует выбрать e и d такие, что е ·d = 1 (mod ϕ(n))
Или e = d -1 (mod ϕ (n))
e и d являются взаимнообратными по умножению по модулю ϕ(n). Заметим, что в соответствии с правилами модульной арифметики, такие взаимнообратные элементы существуют только в том случае, если d (и, следовательно, е) являются взаимнопростыми с ϕ(n). Таким образом, НОД(ϕ(n), d) = 1.
Теперь рассмотрим все элементы алгоритма RSA.
p, q - два простых целых числа- закрыты, выбираемы.
n = p·q - открыто, вычисляемо.
d, НОД (ϕ (n), d) = 1; 1 < d < ϕ (n) - закрыто, вычисляемо.
е = d –1 (mod ϕ (n)) - открыто, выбираемо.
Закрытый ключ состоит из {d, n}, открытый ключ состоит из {e, n}. Предположим, что пользователь А опубликовал свой открытый ключ, и что пользователь В хочет послать пользователю А сообщение М. Тогда В вычисляет С = Ме (mod n) и передает С. При получении этого зашифрованного текста пользователь А расшифрует вычислением М = Сd (mod n).
Суммируем алгоритм RSA:
Создание ключей
Выбрать простые р и q
Вычислить n = p•q
Выбрать d: НОД (ϕ(n), d) = 1; 1 < d <ϕ(n)
Вычислить е: е = d –1 (mod ϕ(n))
Открытый ключ KU = {e, n}
Закрытый ключ KR = {d, n}
Шифрование
Незашифрованное сообщение: М < n
Зашифрованное сообщение: С = Ме (mod n)
Расшифрование
Зашифрованное сообщение: С
Незашифрованное сообщение: М = Сd (mod n)
Рассмотрим конкретный пример:
Выбрать два простых числа: р = 7, q = 17.
Вычислить n = p•q = 7 • 17 = 119.
Вычислить ϕ(n) = (p – 1)•(q – 1) = 96.
Выбрать е так, чтобы е было взаимнопростым с ϕ(n) = 96 и меньше, чем ϕ(n): е = 5.
Определить d так, чтобы d•e = 1 (mod 96) и d < 96.
d = 77, так как 77 • 5 = 385 = 4 • 96 + 1.
Результирующие ключи открытый KU={5,119} и закрытый KR={77,119}.
Например, требуется зашифровать сообщение М = 19.
195 = 66 (mod 119); С = 66.
Для расшифрования вычисляется 6677 (mod 119) = 19.
Вычислительные аспекты
Рассмотрим сложность вычислений в алгоритме RSA при создании ключей и при шифровании / расшифровании.
1. Шифрование / расшифрование
Как шифрование, так и расшифрование включают возведение целого числа в целую степень по модулю n. При этом промежуточные значения будут громадными. Для того чтобы частично этого избежать, используется следующее свойство модульной арифметики:

Другая оптимизация состоит в эффективном использовании показателя степени, так как в случае RSA показатели степени очень большие. Предположим, что необходимо вычислить х16. Прямой подход требует 15 умножений. Однако можно добиться того же конечного результата с помощью только четырех умножений, если использовать квадрат каждого промежуточного результата: х2, х4, х8, х16.
2. Создание ключей
Создание ключей включает следующие задачи:
- Определить два простых числа р и q.
- Выбрать е и вычислить d.
Прежде всего, рассмотрим проблемы, связанные с выбором р и q. Так как значение n = p•q будет известно любому потенциальному противнику, для предотвращения раскрытия р и q эти простые числа должны быть выбраны из достаточно большого множества, т.е. р и q должны быть большими числами. С другой стороны, метод, используемый для поиска большого простого числа, должен быть достаточно эффективным.
Алгоритм, который используется для нахождения простых чисел, выбирает случайное нечетное число из требуемого диапазона и проверяет, является ли оно простым. Если число не является простым, то опять выбирается случайное число до тех пор, пока не будет найдено простое.
Были разработаны различные тесты для определения того, является ли число простым. Это тесты вероятностные, то есть тест показывает, что данное число вероятно является простым. Несмотря на это проверка числа на таких тестах делает вероятность того, что число простой, близкой к единице. Если n "проваливает" тест, то оно не является простым. Если n "пропускает" тест, то n может как быть, так и не быть простым. Если n пропускает много таких тестов, то можно с высокой степенью достоверности сказать, что n является простым. Это достаточно долгая процедура, но она выполняется относительно редко: только при создании новой пары (KU, KR).
На сложность вычислений также влияет то, какое количество чисел будет отвергнуто перед тем, как будет найдено простое число. Результат из теории чисел, известный как теорема простого числа, говорит, что простых чисел, расположенных около n в среднем одно на каждые ln(n)чисел. Таким образом, в среднем требуется проверить последовательность из ln(n) целых, прежде чем будет найдено простое число. Так как все четные числа могут быть отвергнуты без проверки, то требуется выполнить приблизительно ln(n)/2 проверок. Например, если простое число ищется в диапазоне величин 2200, то необходимо выполнить около ln(2200) / 2 = 70 проверок.
Выбрав простые числа р и q, далее следует выбрать значение е так, чтобы НОД (ϕ(n), e) = 1 и вычислить значение d, d = e–1 (mod ϕ(n)). Существует единственный алгоритм, называемый расширенным алгоритмом Евклида, который за фиксированное время вычисляет наибольший общий делитель двух целых и если этот общий делитель равен единице, определяет инверсное значение одного по модулю другого. Таким образом, процедура состоит в генерации серии случайных чисел и проверке каждого относительно 1ϕ(n) до тех пор, пока не будет найдено число, взаимнопростое с ϕ(n). Возникает вопрос, как много случайных чисел придется проверить до тех пор, пока не найдется нужное число, которое будет взаимнопростым с ϕ(n). Результаты показывают, что вероятность того, что два случайных числа являются взаимнопростыми, равна 0.6.
