Технологии туннелирования
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 28.11.2014 | Доступ: свободный | Студентов: 1382 / 124 | Длительность: 23:26:00
ISBN: 978-5-9556-0163-2
Темы: Сетевые технологии, Безопасность
Специальности: Администратор информационных систем, Специалист по безопасности, Администратор коммуникационных систем
Лекция 2:

Алгоритм AES. Режимы выполнения алгоритмов симметричного шифрования. Создание случайных чисел
A
|
версия для печати
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >

Алгоритм Rijndael

В качестве AES был выбран алгоритм Rijndael.

Предварительные математические понятия

Практически все операции Rijndael определяются на уровне байта. Байты можно рассматривать как элементы конечного поля GF (28). Некоторые операции определены в терминах четырехбайтных слов. Введем основные математические понятия, необходимые для обсуждения алгоритма.

Поле GF (2^8)

Элементы конечного поля могут быть представлены несколькими различными способами. Для любой степени простого числа существует един-ственное конечное поле, поэтому все представления GF (28) являются изоморфными. Несмотря на подобную эквивалентность, представление влияет на сложность реализации. Выберем классическое полиномиальное представление.

Байт b, состоящий из битов b7, b6, b5, b4, b3, b2, b1, b0, можно записать в виде полинома с коэффициентами из {0, 1}:

b_7х^7+ b_6х^6 + b_5х^5+ b_4х^4+ b_3х^3 + b_2х^2 + b_1х^1+ b_0

Пример: байт с шестнадцатеричным значением 57 (двоичное значение 01010111) соответствует полиному

х^6 + х^4 + х^2 + х + 1

Определим операцию сложения.

Сумма двух элементов, представленных в виде полинома, является полиномом с коэффициентами, равными сумме по модулю 2 (т.е. 1 + 1 = 0) коэффициентов слагаемых.

Пример: 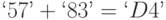‘57’ + ‘83’ = ‘D4’

В полиномиальной нотации:

(х^6 + х^4 + х^2 + х + 1) + (х^7 + х + 1) = х^7 + х^6 + х^4 + х^2

В бинарной нотации:

01010111 + 10000011 = 11010100

Введенное таким образом сложение есть XOR битов в байте.

Выполнены все необходимые условия Абелевой группы: определена операция сложения, обладающая свойством, что каждой паре элементов сопоставляется третий элемент группы, называемый их суммой. Существует нулевой элемент, равный ‘00’, обратный элемент относительно опера-ции сложения. Операция обладает свойствами ассоциативности и коммутативности.

Определим операцию умножения.

В полиномиальном представлении умножение в GF (28) соответствует умножению полиномов по модулю неприводимого двоичного полинома степени 8. Полином называется неприводимым, если он не имеет делителей, кроме 1 и самого себя. Для Rijndael такой полином является m(x):

m(x)= x^8 + x^4 + x^3 + x + 1

или ‘11B’ в шестнадцатеричном представлении.

Пример: ‘57’ \bullet ‘83’ = ‘C1’

Сначала перемножим два полинома

(x^6 + x^4 + x^2 + х + 1) \bullet (x^7 + х + 1) = = x^13 + x^11 + x^9 + x^8 + x^7 + x^6 + x^5 + x^3 + x^2 + x + x^6 + x^4 + x^2 + x + 1= = x^13 + x^11 + x^9 + x^8 + x^6 + x^5 + x^4 + x^3 + 1

Теперь найдем остаток от деления на полином m(x)

(x^8 + x^4 + x^3 + х + 1) \bullet (x^5 + x^3) + x^7 + x^6 + 1 = = x^1^3 + x^1^1 + x^9 + x^8 + x^6 + x^5 + x^4 + x^3 +1

Таким образом, получили

x^1^3 + x^1^1 + x^9 + x^8 + x^6 + x^5 + x^4 + x^8 + 1 mod (x^8 + x^4 + x^3 + х + 1) = = x^7 + x^6 + 1

В этом случае результат будет полиномом не выше 7 степени. В отличие от сложения, простой операции умножения на уровне байтов не существует.

Введенная операция умножения является ассоциативной, существует единичный элемент ‘01’. Для любого двоичного полинома b(x) не выше 7-й степени можно использовать расширенный алгоритм Евклида для вычисления полиномов a(x) и c(x) таких, что

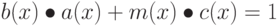
b(x) \bullet a(x) + m(x) \bullet c(x) = 1

Это можно записать как

a(x) \bullet b(x) mod m(x) = 1

или

b^-^1(x) = a(x) mod m(x)

Более того, можно показать, что

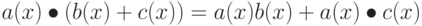
a(x) \bullet (b(x) + c(x)) = a(x) \bulet b(x) + a(x) \bullet c(x)

Из всего этого следует, что множество из 256 возможных значений байта образует конечное поле GF (28) c XOR в качестве сложения и умножением, определенным выше.

Дальше >>
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >

Вопросы и ответы

вопросов: 0