|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Основы теории чисел
1.2 Теория сравнений и ее приложения
1.2.1 Сравнение по модулю
Определение 1.11 Числа, дающие при делении на m одинаковые остатки, называются сравнимыми по модулю  . Обозначение:
. Обозначение:  .
.
Теорема 1.14 (признак сравнимости по модулю) Два целых числа сравнимы по модулю  тогда и только тогда, когда их разность делится на
тогда и только тогда, когда их разность делится на  .
.
Итак, если два целых числа  и
и  сравнимы по модулю
сравнимы по модулю  , то этот факт можно записать разными способами:
, то этот факт можно записать разными способами:  или
или  , где
, где  - целое число, или
- целое число, или  или
или  .
.
Далее, если  , то есть
, то есть  при делении на
при делении на  дает остаток
дает остаток  , то
, то  или
или  . Таким образом, любое целое число
. Таким образом, любое целое число  всегда сравнимо с остатком
всегда сравнимо с остатком  , получающимся при делении его на
, получающимся при делении его на  .
.
Свойства сравнений, не зависящие от модуля
-
Отношение сравнимости удовлетворяет условиям:
- рефлексивности:
 ,
, - симметричности: если
 , то и
, то и  ,
, - транзитивности: если
 , а
, а 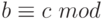 , то
, то  .
.
Отношение, заданное на множестве и обладающее перечисленными свойствами, задает разбиение этого множества на непересекающиеся классы. Применительно к отношению сравнимости по модулю
 это означает: все множество целых чисел разбивается на классы чисел, эти классы не пересекаются. Так, есть класс нуля: это все числа, сравнимые с нулем по модулю
это означает: все множество целых чисел разбивается на классы чисел, эти классы не пересекаются. Так, есть класс нуля: это все числа, сравнимые с нулем по модулю  ,то есть делящиеся на
,то есть делящиеся на  без остатка(включая и само число 0), класс единицы - все числа, дающие остаток 1 при делении на
без остатка(включая и само число 0), класс единицы - все числа, дающие остаток 1 при делении на  , класс 2, ...,класс
, класс 2, ...,класс  . Например, пусть
. Например, пусть  . Получаем следующие классы:
. Получаем следующие классы:![\begin{array}{lcl}
\bar{0}&=&\{\dots,-10, -5, 0, 5, 10, 15, 20,\dots\} \\[1ex]
\bar{1}&=&\{\dots,-9, -4, 1, 6, 11, 16, 21,{\dots}\} \\[1ex]
\bar{2}&=&\{\dots,-8, -3, 2, 7, 12, 17, 22,{\dots}\} \\[1ex]
\bar{3}&=&\{{\dots},-7, -2, 3, 8, 13, 18, 23,{\dots}\} \\[1ex]
\bar{4}&=&\{{\dots},-6, -1, 4, 9, 14, 19, 24,{\dots}\}.
\end{array}](/sites/default/files/tex_cache/6cd40be356bc8150ff13f90b1c25a70e.png)
( 1.2) Определение 1.12 Классы (1.2) называются классами вычетов.
- рефлексивности:
-
Сравнения по одному и тому же модулю можно почленно складывать.
-
Два сравнения по одному и тому же модулю можно почленно вычитать одно из другого.
-
К обеим частям сравнения можно прибавлять одно и то же целое число.
Следствие 1.6 Члены сравнения можно переносить из одной части сравнения в другую с противоположным знаком.
-
Сравнения по одному и тому же модулю можно почленно перемножать.
Следствие 1.7 Обе части сравнения можно возводить в одну и ту же целую неотрицательную степень: если
 и
и  - целое неотрицательное число, то
- целое неотрицательное число, то  .
. - Обе части сравнения можно умножать на одно и то же целое число.
Свойства сравнений, зависящие от модуля
-
Если
 и
и  , то
, то  .
. -
Обе части сравнения и модуль можно умножить на одно и то же целое положительное число.
-
Если
 и
и  , то
, то  .
.Приведем следствия из свойства 9.
Следствие 1.8 Если
 , т. е. если
, т. е. если  , то из
, то из  следует
следует  , а это означает, что обе части сравнения и модуль можно разделить на любой их общий делитель.
, а это означает, что обе части сравнения и модуль можно разделить на любой их общий делитель.Большое значение имеет
Следствие 1.9 Если
 , т. е. если
, т. е. если 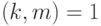 , то из
, то из  следует
следует  , а это означает, что обе части сравнения можно разделить на их общий делитель, если он взаимно прост с модулем.
, а это означает, что обе части сравнения можно разделить на их общий делитель, если он взаимно прост с модулем.Пример 1.9
После деления обеих частей сравнения на .
. получим
получим  .
.
Делить обе части сравнения на число, не взаимно простое с модулем, вообще говоря, нельзя, так как после деления могут получиться числа, несравнимые по данному модулю.
Пример 1.10
 , но
, но  .
. - Если сравнение
 имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
Из рассмотренных свойств сравнений вытекает следующее общее свойство.
-
Пусть
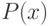 - многочлен с целыми коэффициентами,
- многочлен с целыми коэффициентами,  и
и  - переменные, принимающие целые значения. Тогда если
- переменные, принимающие целые значения. Тогда если  , то
, то  .
.Если
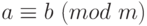 и
и  , то
, то
Таким образом, в сравнении по модулю
Вместе с тем следует обратить внимание на то, что встречающиеся в сравнениях показатели степеней заменять таким образом нельзя: из отдельные слагаемые и множители можно заменять числами, сравнимыми по тому же модулю
отдельные слагаемые и множители можно заменять числами, сравнимыми по тому же модулю  . В частности, все числа, кратные модулю, можно заменять нулями (так как если
. В частности, все числа, кратные модулю, можно заменять нулями (так как если 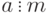 , то
, то 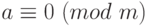 ).
). и
и  не следует, что
не следует, что  .
.
Свойство 11 имеет ряд важных применений. В частности, с его помощью можно дать теоретическое обоснование признаков делимости.
Пример 1.11 Доказать, что при любом натуральном
 число
число  делится на
делится на  .
.Решение. Очевидно, что
 ,
,  ,
,  .
.Возведем первое сравнение в степень
 , второе - в степень
, второе - в степень  , третье - в степень
, третье - в степень  . Полученные сравнения:
. Полученные сравнения:  ,
,  ,
,  , сложим:
, сложим: , то есть
, то есть  делится на
делится на  .
.Пример 1.12 Найти остаток от деления числа
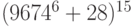 на
на  .
.Решение. Так как
 , то
, то  . Далее,
. Далее,  . Следовательно,
. Следовательно,  . И задача теперь сведена к следующей: найти остаток от деления
. И задача теперь сведена к следующей: найти остаток от деления  на
на  . Воспользуемся сравнениями:
. Воспользуемся сравнениями:  и
и 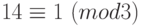 . Из
. Из  следует:
следует:  . А из сравнения
. А из сравнения  следует:
следует: 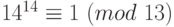 . И так как сравнение имеет место по модулям
. И так как сравнение имеет место по модулям  и
и  , то оно имеет место и по модулю
, то оно имеет место и по модулю  , являющемуся НОК чисел
, являющемуся НОК чисел  и
и  . Итак,
. Итак, 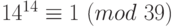 . Но в таком случае
. Но в таком случае  .
.
1.2.2 Возведение в степень по модулю
Пусть  , нам необходимо вычислить
, нам необходимо вычислить  . В дальнейшем перед нами часто будет стоять такая задача с очень большими числами
. В дальнейшем перед нами часто будет стоять такая задача с очень большими числами  ,
,  ,
,  . Очевиднейший способ вычислить
. Очевиднейший способ вычислить  - вычислить произведение
- вычислить произведение  и взять остаток от деления на
и взять остаток от деления на  . Для этого потребуется
. Для этого потребуется  умножений и взятие остатка от деления огромного числа (не всегда даже его хранение в памяти может быть простым) по модулю
умножений и взятие остатка от деления огромного числа (не всегда даже его хранение в памяти может быть простым) по модулю  . Приведём оптимизации для этой задачи.
. Приведём оптимизации для этой задачи.
-
Из свойства

следует, что промежуточные результаты вычислений можно перед хранением брать по модулю
 .
. -
Сгруппируем сомножители в произведении особым образом. Пусть
 ,
,  . Имеем:
. Имеем: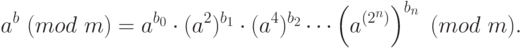
Используя пункт 1, будем все промежуточные результаты хранить по модулю  . Также для деления на 2 мы будем использовать операцию сдвига бит вправо:
. Также для деления на 2 мы будем использовать операцию сдвига бит вправо:

Микропроцессоры имеют специальные инструкции, а языки программирования - специальные операторы для оптимизированного выполнения битового сдвига, которые и следует использовать при реализации данного алгоритма.
Пункт 2 даёт следующий алгоритм возведения в степень по модулю.
Вход:  ,
,  ,
,  - целые неотрицательные числа.
- целые неотрицательные числа.
1) Положить  , ,  , , 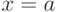 . . |
2) Повторять, пока  : : |
2.1) Если 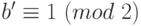 , положить , положить  . . |
2.2) Положить  . . |
2.3) Сдвинуть биты числа  на один вправо (что эквивалентно вычислению на один вправо (что эквивалентно вычислению  ). ). |
Выход:  - результат возведения
- результат возведения  в степень
в степень  по модулю
по модулю  .
.
Также отметим, что на шаге 1 копирование  ,
, 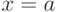 выполняются для того, чтобы не испортить значения
выполняются для того, чтобы не испортить значения  ,
,  , которые могут передаваться в наш алгоритм по указателю или ссылке.
, которые могут передаваться в наш алгоритм по указателю или ссылке.
