Минимальные остовные деревья

Евклидово MST-дерево

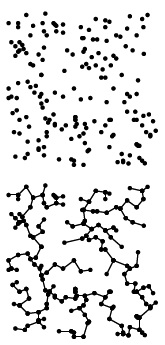
Пусть даны N точек на плоскости, и нужно найти кратчайшее множество линий, соединяющих все эти точки. Эта геометрическая задача называется задачей поиска евклидова MST-дерева (Euclidian MST) (см. рис. 20.18). Один из способов ее решения — построение полного графа с N вершинами и N(N — 1)/2 ребрами — каждую пару вершин соединяет одно ребро, а вес этого ребра равен расстоянию между его вершинами. Затем при помощи алгоритма Прима можно найти MST-дерево за время, пропорциональное N².

Обычно это решение работает слишком медленно. Евклидова задача несколько отличается от задач на графах, которые мы рассматривали выше: в ней все ребра определены неявно. Объем входных данных пропорционален N, так что наш первый вариант решения этой задачи является квадратичным. Исследования показывают, что возможны лучшие решения. Геометрическая структура подразумевает, что большая часть ребер полного графа не понадобится при решении задачи, и большая часть этих ребер не нужна для построения минимального остовного дерева.

Рис. 20.18. Евклидово MST-дерево

Евклидово MST-дерево для заданного множества N точек на плоскости (вверху) — это кратчайшее множество соединяющих их линий (внизу). Эта задача выходит за рамки задач обработки графов, поскольку для ее решения необходимо использовать глобальную геометрическую информацию о точках на плоскости, чтобы не обрабатывать все N² неявных ребер, соединяющих эти точки.

В принципе, триангуляцию Делоне можно вычислить за время, пропорциональное N logN, а затем вычислить евклидово MST-дерево за время, пропорциональное N logN, с помощью либо алгоритма Крускала, либо метода поиска по приоритету. Однако написание программы вычисления триангуляции Делоне — задача не из легких даже для опытного программиста, поэтому на практике такой подход может оказаться слишком трудным для решения подобных задач.

Другие подходы вытекают из геометрических алгоритмов, которые будут рассматриваться в части 7. Для случайно распределенных точек можно поделить плоскость на квадраты таким образом, чтобы каждый квадрат содержал примерно lgN/2 точек, как в программе 3.20 для поиска ближайшей точки. Даже если включить в граф только ребра, соединяющие каждую точку с точками из соседних квадратов, то, скорее всего (хотя и не обязательно), у нас будут все ребра, принадлежащие минимальному остовному дереву; после этого можно эффективно завершить построение с помощью алгоритма Крускала или реализации алгоритма Прима с поиском по приоритету. Примеры на рис. 20.10, 20.13, 20.16 и других подобных рисунках, были построены с использованием именно так ( рис. 20.19). А можно разработать специальную версию алгоритма Прима с использованием алгоритмов поиска ближайшего соседа, чтобы не обрабатывать дальние вершины.

Имея такой набор инструментов и возможности линейных алгоритмов для решения общей задачи вычисления MST, важно помнить о существовании простой нижней границы наших возможностей.

Рис. 20.19. Евклидовы графы ближайших соседей

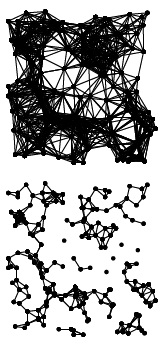
Один из способов вычисления евклидова MST-дерева состоит в построении графа, ребра которого соединяют каждую пару точек, расположенных друг от друга на расстоянии, не превышающем d, подобно графу на рис. 20.8 и т.д. Однако при слишком больших d этот метод дает слишком много ребер (вверху), а если d меньше длины самого длинного ребра в MST, то нельзя гарантировать, что будут доступны все нужные ребра (внизу).

Точные интерпретации этой нижней границы довольно сложны, поскольку базовые операции, используемые для решения этих двух задач (сравнение координат в задаче сортировки и сравнение расстояний в задаче построения MST), различны и поскольку можно использовать методы наподобие поразрядной сортировки и решеточных методов. Однако можно интерпретировать эту границу так: при выполнении сортировки следует считать алгоритм вычисления евклидова MST-дерева с NlgN операциями сравнения оптимальным, если не использовать числовые свойства координат — в этом случае можно надеяться на линейное время выполнения (см. раздел ссылок).

Существует интересная связь между графами и геометрическими алгоритмами, которая вытекает из задачи вычисления евклидова MST-дерева. Многие задачи, которые часто встречаются на практике, могут быть сформулированы либо как геометрические задачи, либо как задачи на графах. Если важно физическое расположение объектов, то можно пользоваться геометрическими алгоритмами, описанными в части VII; но если важнее взаимосвязи между объектами, то обычно удобнее алгоритмы на графах, рассмотренные в данном разделе.

Евклидово MST-дерево находится примерно посередине между двумя этими подходами (на входе геометрические данные, а на выходе — взаимосвязи), и поэтому разработка простых методов вычисления евклидова MST-дерева остается трудной задачей. В "Кратчайшие пути" мы столкнемся с еще одной подобной задачей, которая также находится в этом промежутке, но там евклидов подход допускает гораздо более быстрые алгоритмы, чем соответствующие задачи на графах.

Упражнения

20.81. Приведите контрпример, показывающий, почему не работает следующий метод поиска евклидова MST-дерева: " Упорядочьте точки по их координатам х, потом найдите минимальные основные деревья для первой половины и для второй половины, а затем найдите соединяющие их кратчайшие ребра " .

20.82. Разработайте быструю версию алгоритма Прима для вычисления евклидова MST-дерева для множества равномерно распределенных случайных точек на плоскости, которая основана на игнорировании отдаленных точек до тех пор, пока к ним не приблизится само дерево.

20.83. Разработайте алгоритм, который для заданного множества N точек на плоскости находит множество ребер с мощностью, пропорциональной N, которое наверняка содержит MST и которое достаточно просто вычисляется, чтобы разработать компактную и эффективную реализацию алгоритма.

20.84. Пусть дано множество случайных N точек, равномерно распределенных в единичном квадрате. Эмпирически определите с точностью до двух десятичных цифр значение d, такое, что множество ребер, образованных всеми парами точек на расстоянии не более d, содержит MST с вероятностью 99%.

20.85. Выполните упражнение 20.84 для точек, каждая координата которых получена из гауссова распределения со средним значением 0.5 и со среднеквадратичным отклонением 0.1.

20.86. Опишите, как можно повысить производительность алгоритмов Крускала и Борувки для случая разреженных евклидовых графов.